12．(2010年济南模拟)已知n条直线l₁：x－y+C₁＝0，C₁＝，l₂：x－y+C₂＝0，l₃：x－y+C₃＝0，…，l_n：x－y+C_n＝0(其中C₁<C₂<C₃<…C_n)，在这n条平行直线中，每相邻两条直线之间的距离顺次为2、3、4、…、n.

(1)求C_n；

(2)求x－y+C_n＝0与x轴、y轴围成图形的面积；

(3)求x－y+C_n－1＝0与x－y+C_n＝0及x轴、y轴围成的图形的面积．

解：(1)原点O到l₁的距离d₁为1，原点O到l₂的距离d₂为1+2，…，原点O到l_n的距离d_n为1+2+…+n＝.∵C_n＝d_n，∴C_n＝.

(2)设直线l_n：x－y+C_n＝0交x轴于M，交y轴于N，则

S_△OMN＝|OM|·|ON|＝C_n²＝.

(3)所围成的图形是等腰梯形，由(2)知S_n＝，则有S_n－1＝.

∴S_n－S_n－1＝－＝n³，∴所求面积为n^3.

11．在直线l：3x－y－1＝0上求点P和Q，使得：

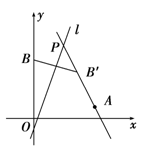(1)P到A(4,1)和B(0,4)的距离之差最大；

(2)Q到A(4,1)和C(3,4)的距离之和最小．

解：(1)如图所示，设点B关于l的对称点B′的坐标为(a，b)，

则k_BB′·k_l＝－1，

即3·＝－1.

∴a+3b－12＝0.①

又由于线段BB′的中点坐标为

，且在直线l上，∴3×－－1＝0，即3a－b－6＝0.②

解①②得a＝3，b＝3，∴B′(3,3)．

于是AB′的方程为＝，即2x+y－9＝0.

解得即l与AB′的交点坐标为P(2,5)．

(2)如图所示，设C关于l的对称点为C′，求出C′的坐标为.

∴AC′所在直线的方程为19x+17y－93＝0，

AC′和l交点坐标为，

故Q点坐标为.

10．在△ABC中，BC边上的高所在直线方程为x－2y+1＝0，∠A的平分线所在直线方程为y＝0，若点B坐标为(1,2)，求点A和C的坐标．

解：由得A(－1,0)．又B(1,2)，∴k_AB＝1.

∵x轴是∠A的平分线，∴k_AC＝－1.

AC直线方程y＝－(x+1)．又BC方程为：y－2＝－2(x－1)，

由得C(5，－6)．

9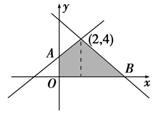．(2010年江苏常州模拟)已知0<k<4，直线l₁：kx－2y－2k+8＝0和直线l₂：2x+k²y－4k²－4＝0与两坐标轴围成一个四边形，则使得这个四边形面积最小的k值为______．

解析：l₁：k(x－2)－2y+8＝0过定点(2,4)，l₂：k²(y－4)＝4－2x也过定点(2,4)，如图，A(0,4－k)，B(2k²+2,0)，S＝×2k²×4+(4－k+4)×2×＝4k²－k+8.当k＝时，S取得最小值．答案：

8．设a、b、c、分别是△ABC中∠A、∠B、∠C所对边的边长，则直线xsinA+ay+c＝0与bx－ysinB+sinC＝0的位置关系是______．

解析：由bsinA－asinB＝0知，两直线垂直．答案：垂直

7．如图，已知A(4,0)、B(0,4)，从点P(2,0)射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是______．

解析：分别求点P关于直线x+y＝4及y轴的对称点，为P₁(4,2)、P₂(－2，0)，由物理知识知，光线所经路程即为P₁P₂＝2.答案：2

6．(2010年苏南四市调研)若函数y＝ax+8与y＝－x+b的图象关于直线y＝x对称，则a+b＝________.

解析：直线y＝ax+8关于y＝x对称的直线方程为x＝ay+8，所以x＝ay+8与y＝－x+b为同一直线，故得，所以a+b＝2.答案：2

5．已知直线l经过点(，2)，其横截距与纵截距分别为a、b(a、b均为正数)，则使a+b≥c恒成立的c的取值范围为________．

解析：设直线方程为+＝1，∴+＝1，a+b＝(a+b)·(+)＝++≥，故c≤.答案：(－∞，]

4．过点P(1,2)作直线l，使直线l与点M(2,3)和点N(4，－5)距离相等，则直线l的方程为________________．

解析：直线l为与MN平行或经过MN的中点的直线，当l与MN平行时，斜率为－4，故直线方程为y－2＝－4(x－1)，即4x+y－6＝0；当l经过MN的中点时，MN的中点为(3，－1)，直线l的斜率为－，故直线方程为y－2＝－(x－1)，即3x+2y－7＝0.答案：3x+2y－7＝0或4x+y－6＝0

3．已知两条直线l₁：ax+by+c＝0，直线l₂：mx+ny+p＝0，则an＝bm是直线l₁∥l₂的________条件．

解析：∵l₁∥l₂⇒an－bm＝0，且an－bm＝0⇒/ l₁∥l₂.答案：必要不充分