
2、李 俊等 主编 数学教育个案学习 华东师范大学出版社 2001
1、中学数学教学参考合订本 陕西师范大学中学教学参考杂志社 2002
3、充分运用“再创造”教学原理开发教材、设计教学。
从本案例的学习中使我得到了一个深刻的启示:即在“新课标”的教学实践中,我要充分运用“再创造”教学原理开发教材、设计教学。这一原理是由荷兰数学家、数学教育家Freudenthal提出并倡导的。那为什么要提出并倡导这一原理呢?Freudenthal教授指出,这样做至少有以下四条教学依据。①通过自身活动所得到的知识与能力比旁人硬塞的理解得更透彻,且掌握得快也善于应用。②发现是一种乐趣,也是人的一种天性,是创新意识培养的必由之路。③通过再创造可以帮助人们形成数学是一种人类活动的观念,而不是把数学当成只有少数人钟爱的智力游戏了。④通过再创造可以帮助学生正确地认识数学体系的形成过程,体会公理系统、形成系统的必要性及作用。而所谓“再创造”的教学原理,就是要求课程设计者和教师不是将数学当作一个现成的体系来教,而应当在教学中充分注意让学生通过再创造的过程来学习数学。它意在改变以往学校数学教育以教师的教为主,以教师传授知识体系为主的做法,提倡教学应以学生的学为主,让学生像数学家那样通过创造数学来学习数学。所以,本人在“新课标”的教学中应该参照知识发展的历史,尽量向学生提供大量的知识背景以供观察、比较和分析,在适当的时机引导学生加强反思,使学生能进行有意识的有目的的再创造活动,尽可能让每位学生获得较多的机会,经历再创造的过程,以获得数学知识创造的亲身体验,让大家都学到自己想学的数学和获得人人想学的数学。
时代在改变,我想我们也应该与时俱进与时代同行,为学生做一点我们力所能及的事情,也从中让我们得到启发得到成长,让自己活得更有价值更有意义,使我们的教师生涯充满意义和乐趣、充满时代感。
参考文献
2、转变教育观念,改善知识结构。
从“重知识传授”向“重学生发展”转变,由“重结果”向“重过程”转变。即在教学过程中,不仅使学生掌握一些基本的数学结论,更重要的是让学生理解数学问题是怎样提出的,概念是如何在具体的背景中形成的,结论是怎样探索和猜测得到的,证明的思路和计算的想法是怎样得到的等等。从而实现学生的数学学习由被动接受“结果”向主动构建“过程”的转化。由于教学观念的转变,我们还必须改变自己的知识结构。使自己不仅要有扎实的数学专业知识,深厚的教育理论修养,广阔的教育前沿视野,敏感的教育问题意识,而且应有过硬的教育科研能力和研究学生的数学学习心理,只有这样才能使我们有效地提供给学生解决问题的思路和方法。
通过本案例的学习,本人对“新课标”的教学实施有了进一步的认识,以后将会围绕以下几方面开展教学工作:
1、把“新课标”教学实践当作一项科研工作,与大家共同努力。
因为时代在不断的变化,要求我们要从“教育工作者”向“教研工作者”转变,当一位教研型的教师,所以我应该把教学工作看成是一项教育研究工作。在教学的过程中做好有关素材的收集与整理工作,做好“新课标”教学策略的调整工作,与所有有志于“新课标”改革的老师共同努力,力争做到最好。
在解决问题的过程中,张老师绝大部分是让学生进行探究的,但有一个地方本人认为他可以更加大胆的放手让学生探究。如刚好计算出 的面积等于正方形ABCD的面积的一半时,他无意中已用设问的方式道出了“
的面积等于正方形ABCD的面积的一半时,他无意中已用设问的方式道出了“ 的面积与小正方形面积无关”这一本质问题。从表面上看,好像是在引导学生思考,实际上是牵着学生的鼻子走,没有让学生进行真正的探索和让学生根据自己的实际建构提出问题,没有真正达到开发学生思维潜力的目的,反而把原本有探究价值且可由学生独立探究的问题分解为一小块一小块。其实,张老师可直接问学生:“你们由此发现了怎样的事实?”而不要把实质问题“
的面积与小正方形面积无关”这一本质问题。从表面上看,好像是在引导学生思考,实际上是牵着学生的鼻子走,没有让学生进行真正的探索和让学生根据自己的实际建构提出问题,没有真正达到开发学生思维潜力的目的,反而把原本有探究价值且可由学生独立探究的问题分解为一小块一小块。其实,张老师可直接问学生:“你们由此发现了怎样的事实?”而不要把实质问题“ 的面积与小正方形面积无关”用设问的方式导出来。我想,若能长期这样训练下去必定会提高学生的“数感”和对数学的敏感度。
的面积与小正方形面积无关”用设问的方式导出来。我想,若能长期这样训练下去必定会提高学生的“数感”和对数学的敏感度。
在本案例中,还有一个问题值得我们深思:就是在解决完一道例题后我们教师该做怎样的工作,使学生有进一步的收获?在本案例中没有反映出这一点。本人觉得:问题解决完后教师应带领学生进行深入的自我总结,把问题上升到理性认识。在解决完本例题后,若张老师能带领学生回过头再一次用审视的眼光评析他们的所做、评析他们的思考方式、评析他们的所得,那该多好呀!
为什么本人会有这种想法呢?因为本人觉得从高一点的角度看,解题的目的主要有二个:一是学科意义上的价值,即通过解题,进一步熟悉、理解所学内容,在内容间建立起联系;二是人生意义上的价值,也是根本所在,即通过解题,让学生从成功中发现自我,培养自信、坚强、忍耐的品格。所以,我们教师应该帮助学生养成自觉反思的习惯,总结解题过程中的经验,学会寻找新旧知识间的联系,寻找解决此类问题的一般解法和在解决问题的过程中如何突破自己思维框架等等,把思维的“网口”有目的地拉大,逐步培养思维的创造力。
最后,我还在想:若我们教师能真正给时间给空间学生进行探究,我们整个教育将会是怎样的一番景象呢?这还有待我们大家去探讨。
案例中,学生能在教师的引导下,不但能在对图形进行直观观察的基础上用割补法、相似的性质、等底等高面积法等方法解决问题,而且会由25与50的关系大胆猜想:无论在什么情况下 的面积刚好等于正方形ABCD的面积的一半,且与小正方形的面积无关。最难能可贵的是学生在解决此问题时能利用解决问题的特殊法过渡到一般法。并且学生F能从纷繁复杂的图形中观察出“等底等高”这一主要的特征,并用这一特征轻松地说明、解决问题。在整个过程中处处体现了学生主动探索,教师适当引导的融洽交流情景,学生的思维也得到了充分的拓展。这说明了一个问题:若我们教师能积极创设情景,不断给学生思维的契机,处处设疑、激疑、释疑,我想这样必定会激发学生学习的热情、好奇心,从而引发学生创造性思维。
的面积刚好等于正方形ABCD的面积的一半,且与小正方形的面积无关。最难能可贵的是学生在解决此问题时能利用解决问题的特殊法过渡到一般法。并且学生F能从纷繁复杂的图形中观察出“等底等高”这一主要的特征,并用这一特征轻松地说明、解决问题。在整个过程中处处体现了学生主动探索,教师适当引导的融洽交流情景,学生的思维也得到了充分的拓展。这说明了一个问题:若我们教师能积极创设情景,不断给学生思维的契机,处处设疑、激疑、释疑,我想这样必定会激发学生学习的热情、好奇心,从而引发学生创造性思维。
而对于教师来说,本人觉得:首先张老师能打破传统习题课的框架,将解题的过程成为学生自己探索和发现的过程,而不是教师对求解模式的介绍过程。在这个过程中,引导学生深入思考、解决问题,并抓住时机引导学生探索出 的面积与小正方形的面积无关这一隐含性结论;其次,他能够带领学生对一个问题进行横纵向地深入学习、探究,而不是像我们一般的习题课那样只是为了解题而解题。并且能在教学中及时渗透解决问题的一般法与特殊法、直接法与间接法、割补法、分类讨论等数学思想方法。总的来说,整个案例体现了张老师教学过程思路清晰,突出思维的主题,设问架桥,引导学生思维层层拔高,是符合“新课标”思想要求,符合新的教育理念和教学策略的,我们应该学习和借鉴他的做法。
的面积与小正方形的面积无关这一隐含性结论;其次,他能够带领学生对一个问题进行横纵向地深入学习、探究,而不是像我们一般的习题课那样只是为了解题而解题。并且能在教学中及时渗透解决问题的一般法与特殊法、直接法与间接法、割补法、分类讨论等数学思想方法。总的来说,整个案例体现了张老师教学过程思路清晰,突出思维的主题,设问架桥,引导学生思维层层拔高,是符合“新课标”思想要求,符合新的教育理念和教学策略的,我们应该学习和借鉴他的做法。
问题背景:在教学“有关简单图形面积的计算”内容后安排的一节复习课。
 问题:一个面积为50
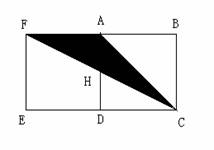
问题:一个面积为50 的正方形与一个小正方形并排放在一起(图1),试求出
的正方形与一个小正方形并排放在一起(图1),试求出 的面积。
的面积。
教师:同学们想想看,可如何求出 的
的
面积?
学生A:只需求出 与
与 的面积,再相加即可。
的面积,再相加即可。
教师:不错,但是求解的关键是什么呢?
学生A:关键是求出H点在AD上的确切位置。 (图1)
教师:那么如何确定H的位置呢?
学生A:可以设 ∽
∽
得 ,即
,即 ,由此确定了点H的位置。
,由此确定了点H的位置。
教师:A同学从 的两个构成部分着手,找到了解决问题的一种思路,习惯上我们称之为直接法(加强语气),再想想还有其他方法吗?
的两个构成部分着手,找到了解决问题的一种思路,习惯上我们称之为直接法(加强语气),再想想还有其他方法吗?
学生B:可先计算出四边形ACEF以及 的面积,再求出
的面积,再求出 的面积。
的面积。
教师:很好!采用了间接计算的方法。
学生C(举手):也可以延长EF交BA的延长线于N,利用四边形BCEN的面积减去 、
、 、
、 的面积(不少同学纷纷点头,显然此法也比较容易让人理解、接受)。
的面积(不少同学纷纷点头,显然此法也比较容易让人理解、接受)。
教师:刚才同学们列举了三种计算面积的思想,下面请大家计算一下 的面积(要求:基础一般的同学先用后两种方法计算,基础较好的同学先按第一种方法计算)。
的面积(要求:基础一般的同学先用后两种方法计算,基础较好的同学先按第一种方法计算)。
学生:(四至五分钟) 的面积等于25
的面积等于25 。
。
教师:用不同的方法计算 的面积都等于25
的面积都等于25 ,而大正方形的面积是50
,而大正方形的面积是50 ,同学们看看有什么发现?
,同学们看看有什么发现?
学生(众):刚好是大正方形面积的一半。
学生(少数):会不会是一种巧合呢?(几分钟后)
 学生(个别):不是巧合,刚好一半。
学生(个别):不是巧合,刚好一半。
教师:那么如何判断 的面积与小正方形面积
的面积与小正方形面积
无关?
学生D:可以利用特殊法验证,如小正方形与大正方形的边长相等时(图2),容易计算 ,其结果不变,因此可以说明
,其结果不变,因此可以说明 的面积与小正方形面积无关!
(图2)
的面积与小正方形面积无关!
(图2)
(不少同学点头赞同)
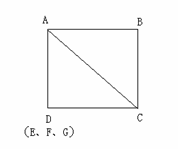 学生E:(迫不及待地)还有一种特殊法,当小正方形的边长逐渐变小至D、E、F、G四点合一时(图3),
学生E:(迫不及待地)还有一种特殊法,当小正方形的边长逐渐变小至D、E、F、G四点合一时(图3),  。
。
教师:刚才两位同学很巧妙地运用了特殊化思想求
出了 的面积,看来方法不少。同学们再想想看,
当小正方形的边长大于AB时,
的面积,看来方法不少。同学们再想想看,
当小正方形的边长大于AB时, 的面积也等25
的面积也等25 吗?
吗?
学生:……(继续思考) (图3)
教师:画出图形,再观察思考,看看情况有无变化?
学生F:连接DF,可证得FD∥AC,所以点F到AC的距离等于D到AC的距离,所以 结果仍没有改变。
结果仍没有改变。
 教师:太妙了,此法不但简单地算出了结果,而且严格地
教师:太妙了,此法不但简单地算出了结果,而且严格地
证明了 的面积的确与小正方形EFGD的大小无关,真是一个漂亮的证法。那么请问这位同学,你又是如何发现这种方法的呢?
的面积的确与小正方形EFGD的大小无关,真是一个漂亮的证法。那么请问这位同学,你又是如何发现这种方法的呢?
学生F:我画了两个比ABCD大的正方形DEFG和正方形
DIJK(图4),发现JF、AC有平行关系。根据同底等高,所以 与
与 面积相等。
面积相等。
教师:……(给了这位学生充分的评价)。 图4
(五)明清时期的科技和文学艺术
1.科技成果:①明朝徐光启编撰《农政全书》,对我国传统农学进行总结;②李时珍编《本草纲目》,总结我国16世纪以前的药物和成就,被誉为“东方药物巨典”。
2.文学艺术成就:①小说呈现空前繁荣局面,《三国演义》、《水浒转》、《西游记》、《红楼梦》问世;②传奇的演唱形成昆曲一统的局面,汤显祖的《牡丹亭》是明传奇最出色的作品;③在徽剧与汉剧融合,兼收昆曲、秦腔的基础上形成京剧,涌现“同光十三绝”的著名艺人;④明代徐渭的《牡丹蕉石图》,清代郑板桥的《墨兰图》是写意画中的精品。
[教学反思]
(四)明清时期儒学的新发展
1.明朝中期,王阳明发展了南宋时期陆九渊的学说,成为心学的集大成者;他把程朱理学发展为“心学”,宣扬人心是世界万物的本原,“心即理”、“心外无物”的主观唯心论的宇宙观;提出“致良知”的学说,进一步发挥儒家“仁”的思想。
2.明朝后期,李贽的“离经叛道”。表现在:他自称异端,认为是非标准依照时代变化而变化,反对以孔子的是非为标准;他批判道学家“存天理,灭人欲”的虚假说教,强调人的正当私欲。李贽的思想在一定程度上反映了资本主义萌芽时期的要求。
3.明末清初,黄宗羲、顾炎武、王夫之的民主启蒙思想。黄宗羲主张“天下为主,君为客”,君主专制是“天下之大害”,“工商皆民生之本”。顾炎武主张“天下兴亡,匹夫有责”,“经世致用”,到实践中求得真知。王夫之主张世界是物质的,物质是第一性的,物质不断变化是万物发展的规律;他具有朴素的辩证法思想。他的唯物思想,启示了近代人们的思维方法,具有划时代的意义。
评价:他们的思想主张是明清时期封建制度渐趋衰落、商品经济发展和资本主义萌芽这两大时代发展趋势在思想上的反映,他们的进步思想是对传统儒学的批判继承,促使我国传统文化重新焕发生机,对后世产生了巨大影响。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com