4.与唐代长安城相比，明清时期的北京城

①面积小　　　　　　　　 ②营业时间固定

③商业更加繁荣　　　　　 ④建筑布局突出了皇权

A．①③④　　 B. ①②　 C. ②③　　　 D．③④

3.下列建筑属于我国古代建筑成熟时期的是

A．赵州桥　　 B.天津蓟县独乐寺　 C．山西应县木塔　　　 D.卢沟桥　

2. “尽道隋亡为此河,至今千里赖通波。若无水殿龙舟事,共禹论功不较多!”对此理解正确的是

①大运河开凿导致隋朝灭亡　　　　 ②大运河开凿加强了南北之间经济文化的联系

③到扬州游玩也是开凿大运河的目的之一 ④推动了经济重心的南移

A．①③④　　 B. ①②　 C. ②③　　　 D．②③④

1.秦始皇下令开凿的灵渠

A．便利了中原和秦岭以南地区的经济文化交流　　

B．沟通了湘江和长江两大水系

C．是世界最早古老人工运河

D．为秦统一越族地区创造了条件

[课题引入]

例：设a>b>c，a+b+c=1，a²+b²+c²=1.求证：1<a+b<。 　证明：依题设有a+b=1-c；　①　　　　　　 a²+b²=1-c²；　② ①²－②得ab=c²-c。　　③ 　由①、③两式说明：a、b是关于x的一元二次方程：x²-(1-c)x+c²-c=0，④的两个不相等的实根，且因为已知a>b>c，表明方程④的两根都大于c。　

设f(x)=x²-(1－c)x+c²-c，∴，由①知，。

从该例中抽象出解题方法为：构造法，这也是我们今天要讲解的课题：用构造法解题。它在数学解题过程中有着较为广泛的应用。

构造法：就是根据题设条件和结论的特殊性，构造出一些新的数学形式，并借助它认识与解决原问题的一种思想方法。

用构造法解题的关键在于寻找到合理的数学模型。

[例题部分]

例1 　设x、y∈R，且满足，求x+y的值。

解：构造函数f(t)=t²⁰⁰³+2002t，易知f(t)是R上的奇函数也是单调函数，由此可得：f(x-1)= -f(y-2)，∴f(x-1)=f(2-y)，∴x-1=2-y，∴x+y=3。

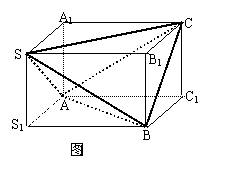例2 　四面体S-ABC的三组对棱分别相等，且依次为，，5，试求四面体

S-ABC的体积。

解：如图1，构造长方体SA₁CB₁-S₁AC₁B ，分别连结　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

SA、SB、SC、AB、BC、CA。

设长方体的三度分别为：、、。

令，

则有。

由图1，则四面体S-ABC的体积为长方体的体积减去四个等积的三棱锥体积，

∴=8。

例3　 求方程a+b+c+d=6有多少组正整数解？

解：构造模式：有6个形状、大小、颜色完全相同的球分成四组，每组中至少有一个球的分法有多少种：○　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ○　 ○　 ○　 ○　 ○。

该问题利用构造模型转化为了一个组合问题，实际上是在五个空中插入3个隔板，共

=10种正整数解。

例4　 设x，y均为正实数，证明：不等式。

证明：① 当x=y时，；

② 当x≠y时，不失一般性，设x>y>0，并取y=m，则x∈(m，+∞)，

设g(x)=xlnx+ylny-(x+y)In，即g(x)=xlnx-(x+m)ln+mlnm，(x∈(m，+∞))

又∵，

∵2x>x+m，∴，∴，∴g(x)在(m，+∞)上单调递增，又g(m)=0，∴g(x)>0，即xlnx-(x+m)In+mlmm>0，∴，即。

综合①②知：有。

例5　 　对一切非零自然数n，求证：

证明： 构造数列{an}，使其通项为

又∵ ，

，∴ 对一切自然数n，都有a_n≥a₁>1，即

∴。

本题一般用数学归纳法证明，但应用构造思想求解，更有情趣，更见功力.

[课堂小结]

(1)用构造法解题，可构造表达式，构造图形等，在构造表达式中我们又可构造函数，构造数列等进行解题。

(2)应用好构造法的关键有两点：① 要有明确的方向，即为什么目的而构造；② 要弄清条件的本质特点，以便重新进行逻辑组合。

(3)运用构造法解题，关键在于寻找到合理的数学模型，一旦运用成功，它所呈现的是问题的本质规律和数学内在的美，往往给人耳目一新的感觉，同时也告诉我们大家数学是一门创造性的艺术，蕴含着丰富的美，而灵活、巧妙的构造令人拍手叫绝。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2007-11-20

教学重点：理解构造法。

教学难点：掌握并应用构造法解题。

理解并掌握构造法解题的原理与步骤；并通过对构造法解题的讲解，培养学生的创新思维能力。

21．请以“传递”为题，写一篇文章。

要求：① 除诗歌、戏剧外，文体不限；

② 要突出自己的体验和感悟，不得抄袭；

　　　　　　　　　　　　　　　　　　　　　　 ③ 不少于600字；

④ 文中不能出现真实的校名和人名。

江苏省常州市二○○九年初中毕业、升学统一考试