例3. 解不等式

　　 解：若令则

　　 ∵，且

　　 ∴

　　 ∴不等式化为

　　 即

　　 ∴

　　 解得

　　 从而

　　 即

　　 ∴不等式的解集是

　 例2. 已知a，b，c为正整数，且，求的值。

　　 解：因为不等式两边均为正整数，所以不等式与不等式等价，这个等价不等式又可转化为。

　　 ∴

　　 ∴

　　 即a=2，b=3，c=6

　　 评注：将等式与不等式对应等价转化，是转化数学问题的常用且非常有效的手段。

　 例1. 已知不等式，(1)求该不等式中x的集合；(2)若1不是不等式的解，0是不等式的解，求k的取值范围。

　　 解：(1)

　　 当k>1时，解集为

　　 当时，解集为

　　 当k<1时，解集为

　　 (2)

　　 所以

　　 评注：当一次项系数为0时，不等式成为两个常数比较大小的形式，与x取值无关。因此，不等式的解集为R(不等式成立时)或(不等式不成立时)。

　 例5. 已知x，y，，且，求的最大值。

　　 解：因为x，y，，且

　　 则

　　 当且仅当及时，取得等号

　　 此时

　　 所以

高三数学数学思想在不等式问题中的体现

　 例4. 求函数的最大值。

　　 解：

　　 当且仅当

　　 即时取等号

　　 所以的最大值为

　　 评注：形如型的最值问题，可考虑分子常数化。

　 例3. 设，求函数的最大值。

　　 分析：挖掘隐含条件，为能构造出和为定值，需要考虑y²。

　　 解：因为，所以

　　 所以

　 　当且仅当

　　 即时取等号

　　 所以

　 例1. 求函数的最小值。

　　 解：因为

　　 所以

　　 当且仅当

　　 即时取得等号

　　 故

　　 评注：对“5x”进行恰当地拆分，才能实现“三相等”。

　 例2. 求函数的值域。

　　 分析：因分母的次数低于分子的次数，将其化为型，再利用平均值不等式求最值。

　　 解：

　　 当x+1>0

　　 即x>－1时，

　　 当且仅当

　　 即时取等号

　　 当

　　 即时，

　　 当且仅当

　　 即时取等号

　　 故函数的值域为

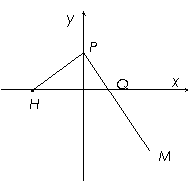
21、已知点H(－3，0)，点P在轴上，点Q在轴的正半轴上，点M在直线PQ上，且满足， .

(1)当点P在轴上移动时，求点M的轨迹C；

(2)过定点作直线交轨迹C于

A、B两点，E是D点关于坐标原点O的对称点，

试问吗？若相等，请给出证明，若不相等，说明理由。

瑞安中学2008学年第二学期高二年级期中考试

20、 如图，四棱锥P-ABCD的底面为菱形且，PA⊥底面ABCD，AB=2，PA=，E为PC的中点。

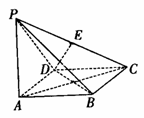(1)求直线DE与平面PAC所成角的大小；

(2)求点到平面的距离。

19、已知空间四点O(0，0，0)，A(2，0，0)，B(0，2，0)，C(0,0,4),

(1) 若直线上的一点满足，求点的坐标.

(2)若平面上的一点满足⊥面，求点的坐标.