3、将v₁ 、v的替代式代入①式解v₂即可。结果：v₂ =

(学生活动)思考：球形铰链触地前一瞬，左球、铰链和右球的速度分别是多少？

解：由两杆不可形变，知三球的水平速度均为零，θ为零。一个能量方程足以解题。

答：0 、 、0 。

(学生活动)思考：当两杆夹角为90°时，右边小球的位移是多少？

解：水平方向用“反冲位移定式”，或水平方向用质心运动定律。

答： 。

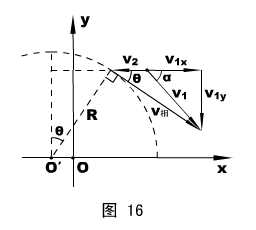进阶应用：在本讲模型“四、反冲……”的“进阶应用”(见图8)中，当质点m滑到方位角θ时(未脱离半球)，质点的速度v的大小、方向怎样？

解说：此例综合应用运动合成、动量守恒、机械能守恒知识，数学运算比较繁复，是一道考查学生各种能力和素质的难题。

据运动的合成，有：

　= 　+ 　= 　-

其中必然是沿地面向左的，为了书写方便，我们设其大小为v₂ ；必然是沿半球瞬时位置切线方向(垂直瞬时半径)的，设大小为v_相 。根据矢量减法的三角形法则，可以得到(设大小为v₁)的示意图，如图16所示。同时，我们将v₁的x、y分量v_1x和v_1y也描绘在图中。

由图可得：v_1y =(v₂ + v_1x)tgθ　　　　　　　　　　　　　　　　 ①

质点和半球系统水平方向动量守恒，有：Mv₂ = mv_1x　　　　　　　　 ②

对题设过程，质点和半球系统机械能守恒，有：mgR(1-cosθ) = M + m ，即：

mgR(1-cosθ) = M + m( + )　　　　　　　　　　 ③

三个方程，解三个未知量(v₂ 、v_1x 、v_1y)是可行的，但数学运算繁复，推荐步骤如下--

2、在回到③、④两式，得：

v₁ = v₂ ,　 v = v₂

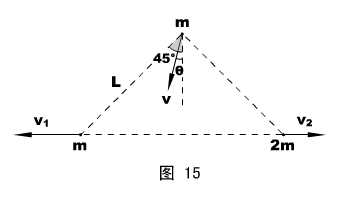
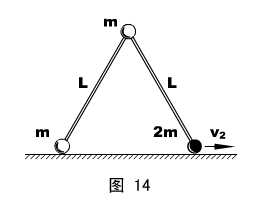物理情形：如图14所示，两根长度均为L的刚性轻杆，一端通过质量为m的球形铰链连接，另一端分别与质量为m和2m的小球相连。将此装置的两杆合拢，铰链在上、竖直地放在水平桌面上，然后轻敲一下，使两小球向两边滑动，但两杆始终保持在竖直平面内。忽略一切摩擦，试求：两杆夹角为90°时，质量为2m的小球的速度v₂ 。

模型分析：三球系统机械能守恒、水平方向动量守恒，并注意约束关系--两杆不可伸长。

(学生活动)初步判断：左边小球和球形铰链的速度方向会怎样？

设末态(杆夹角90°)左边小球的速度为v₁(方向：水平向左)，球形铰链的速度为v(方向：和竖直方向夹θ角斜向左)，

对题设过程，三球系统机械能守恒，有：

mg( L-L) = m + mv² + 2m　　 ①

三球系统水平方向动量守恒，有：

mv₁ + mvsinθ= 2mv₂　　　　　　　　 ②

左边杆子不形变，有：

v₁cos45°= vcos(45°-θ)　　　　　 ③

右边杆子不形变，有：

vcos(45°+θ) = v₂cos45°　　　　 ④

四个方程，解四个未知量(v₁ 、v₂ 、v和θ)，是可行的。推荐解方程的步骤如下--

1、③、④两式用v₂替代v₁和v ，代入②式，解θ值，得：tgθ= 1/4

物理情形：如图13所示，直角形的刚性杆被固定，水平和竖直部分均足够长。质量分别为m₁和m₂的A、B两个有孔小球，串在杆上，且被长为L的轻绳相连。忽略两球的大小，初态时，认为它们的位置在同一高度，且绳处于拉直状态。现无初速地将系统释放，忽略一切摩擦，试求B球运动L/2时的速度v₂ 。

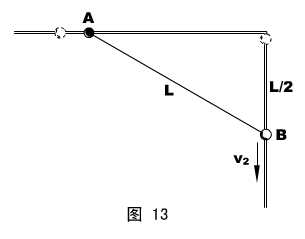模型分析：A、B系统机械能守恒。A、B两球的瞬时速度不等，其关系可据“第三部分”知识介绍的定式(滑轮小船)去寻求。

(学生活动)A球的机械能是否守恒？B球的机械能是否守恒？系统机械能守恒的理由是什么(两法分析：a、“微元法”判断两个W_T的代数和为零；b、无非弹性碰撞，无摩擦，没有其它形式能的生成)？

由“拓展条件”可以判断，A、B系统机械能守恒，(设末态A球的瞬时速率为v₁ )过程的方程为：

m₂g = 　+ 　　　　　　①

在末态，绳与水平杆的瞬时夹角为30°，设绳子的瞬时迁移速率为v ，根据“第三部分”知识介绍的定式，有：

v₁ = v/cos30°, v₂ = v/sin30°

两式合并成：v₁ = v₂ tg30°= v₂/　　 ②

解①、②两式，得：v₂ =

4、如图10所示，双手用等大反向的力F压固定汽缸两边的活塞，活塞移动相同距离S，汽缸中封闭气体被压缩。施力者(人)是否做功？

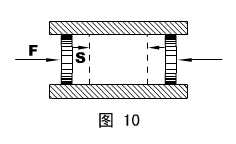在以上四个事例中，S若取作用点位移，只有第1、2、4例是做功的(注意第3例，楼梯支持力的作用点并未移动，而只是在不停地交换作用点)，S若取物体(受力者)质心位移，只有第2、3例是做功的，而且，尽管第2例都做了功，数字并不相同。所以，用不同的判据得出的结论出现了本质的分歧。

面对这些似是而非的“疑难杂症”，我们先回到“做功是物体能量转化的量度”这一根本点。

第1例，手和讲台面摩擦生了热，内能的生成必然是由人的生物能转化而来，人肯定做了功。S宜取作用点的位移；

第2例，求拉力的功，在前面已经阐述，S取作用点位移为佳；

第3例，楼梯不需要输出任何能量，不做功，S取作用点位移；

第4例，气体内能的增加必然是由人输出的，压力做功，S取作用点位移。

但是，如果分别以上四例中的受力者用动能定理，第1例，人对讲台不做功，S取物体质心位移；第2例，动能增量对应S取L/2时的值--物体质心位移；第4例，气体宏观动能无增量，S取质心位移。(第3例的分析暂时延后。)

以上分析在援引理论知识方面都没有错，如何使它们统一？原来，功的概念有广义和狭义之分。在力学中，功的狭义概念仅指机械能转换的量度；而在物理学中功的广义概念指除热传递外的一切能量转换的量度。所以功也可定义为能量转换的量度。一个系统总能量的变化，常以系统对外做功的多少来量度。能量可以是机械能、电能、热能、化学能等各种形式，也可以多种形式的能量同时发生转化。由此可见，上面分析中，第一个理论对应的广义的功，第二个理论对应的则是狭义的功，它们都没有错误，只是在现阶段的教材中还没有将它们及时地区分开来而已。

而且，我们不难归纳：求广义的功，S取作用点的位移；求狭义的功，S取物体(质心)位移。

那么我们在解题中如何处理呢？这里给大家几点建议： 1、抽象地讲“某某力做的功”一般指广义的功；2、讲“力对某物体做的功”常常指狭义的功；3、动能定理中的功肯定是指狭义的功。

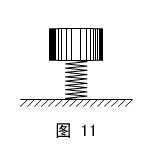
当然，求解功地问题时，还要注意具体问题具体分析。如上面的第3例，就相对复杂一些。如果认为所求为狭义的功，S取质心位移，是做了功，但结论仍然是难以令人接受的。下面我们来这样一个处理：将复杂的形变物体(人)看成这样一个相对理想的组合：刚性物体下面连接一压缩的弹簧(如图11所示)，人每一次蹬梯，腿伸直将躯体重心上举，等效为弹簧将刚性物体举起。这样，我们就不难发现，做功的是人的双腿而非地面，人既是输出能量(生物能)的机构，也是得到能量(机械能)的机构--这里的物理情形更象是一种生物情形。本题所求的功应理解为广义功为宜。

以上四例有一些共同的特点：要么，受力物体情形比较复杂(形变，不能简单地看成一个质点。如第2、第3、第4例)，要么，施力者和受力者之间的能量转化不是封闭的(涉及到第三方，或机械能以外的形式。如第1例)。以后，当遇到这样的问题时，需要我们慎重对待。

(学生活动)思考：足够长的水平传送带维持匀速v运转。将一袋货物无初速地放上去，在货物达到速度v之前，与传送带的摩擦力大小为f ，对地的位移为S 。试问：求摩擦力的功时，是否可以用W = fS ？

解：按一般的理解，这里应指广义的功(对应传送带引擎输出的能量)，所以“位移”取作用点的位移。注意，在此处有一个隐含的“交换作用点”的问题，仔细分析，不难发现，每一个(相对皮带不动的)作用点的位移为2S 。(另解：求货物动能的增加和与皮带摩擦生热的总和。)

答：否。

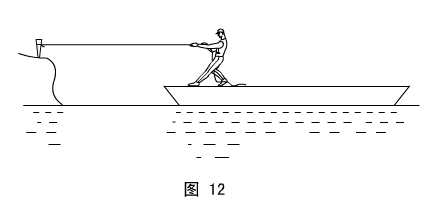
(学生活动)思考：如图12所示，人站在船上，通过拉一根固定在铁桩的缆绳使船靠岸。试问：缆绳是否对船和人的系统做功？

解：分析同上面的“第3例”。

答：否。

3、人登静止的楼梯，从一楼到二楼。楼梯是否做功？

2、在本“部分”第3页图1的模型中，求拉力做功时，S是否可以取绳子质心的位移？

在求解功的问题时，有时遇到力的作用点位移与受力物体的(质心)位移不等，S是取力的作用点的位移，还是取物体(质心)的位移呢？我们先看下面一些事例。

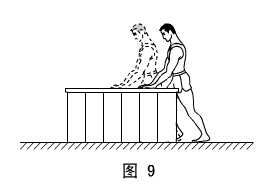
1、如图9所示，人用双手压在台面上推讲台，结果双手前进了一段位移而讲台未移动。试问：人是否做了功？

物理情形：如图4所示，长度为L、质量为M的船停止在静水中(但未抛锚)，船头上有一个质量为m的人，也是静止的。现在令人在船上开始向船尾走动，忽略水的阻力，试问：当人走到船尾时，船将会移动多远？

(学生活动)思考：人可不可能匀速(或匀加速)走动？当人中途停下休息，船有速度吗？人的全程位移大小是L吗？本系统选船为参照，动量守恒吗？

模型分析：动量守恒展示了已知质量情况下的速度关系，要过渡到位移关系，需要引进运动学的相关规律。根据实际情况(人必须停在船尾)，人的运动不可能是匀速的，也不可能是匀加速的,运动学的规律应选择S = t 。为寻求时间t ，则要抓人和船的位移约束关系。

对人、船系统，针对“开始走动→中间任意时刻”过程，应用动量守恒(设末态人的速率为v ，船的速率为V)，令指向船头方向为正向，则矢量关系可以化为代数运算，有：

0 = MV + m(-v)

即：mv = MV

由于过程的末态是任意选取的，此式展示了人和船在任一时刻的瞬时速度大小关系。而且不难推知，对中间的任一过程，两者的平均速度也有这种关系。即：

m = M　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

设全程的时间为t ，乘入①式两边，得：mt = Mt

设s和S分别为人和船的全程位移大小，根据平均速度公式，得：m s = M S　　　　 ②

受船长L的约束，s和S具有关系：s + S = L　　　　　　　　　　　　　　　　　 ③

解②、③可得：船的移动距离 S =L

(应用动量守恒解题时，也可以全部都用矢量关系，但这时“位移关系”表达起来难度大一些--必须用到运动合成与分解的定式。时间允许的话，可以做一个对比介绍。)

另解：质心运动定律

人、船系统水平方向没有外力，故系统质心无加速度→系统质心无位移。先求出初态系统质心(用它到船的质心的水平距离x表达。根据力矩平衡知识，得：x = )，又根据，末态的质量分布与初态比较，相对整体质心是左右对称的。弄清了这一点后，求解船的质心位移易如反掌。

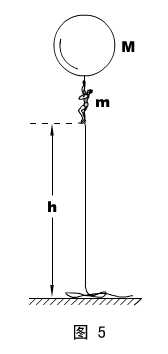(学生活动)思考：如图5所示，在无风的天空，人抓住气球下面的绳索，和气球恰能静止平衡，人和气球地质量分别为m和M ，此时人离地面高h 。现在人欲沿悬索下降到地面，试问：要人充分安全地着地，绳索至少要多长？

解：和模型几乎完全相同，此处的绳长对应模型中的“船的长度”(“充分安全着地”的含义是不允许人脱离绳索跳跃着地)。

答：h 。

(学生活动)思考：如图6所示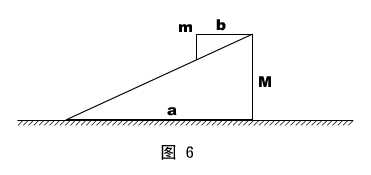，两个倾角相同的斜面，互相倒扣着放在光滑的水平地面上，小斜面在大斜面的顶端。将它们无初速释放后，小斜面下滑，大斜面后退。已知大、小斜面的质量分别为M和m ，底边长分别为a和b ，试求：小斜面滑到底端时，大斜面后退的距离。

解：水平方向动量守恒。解题过程从略。

答：(a－b)。

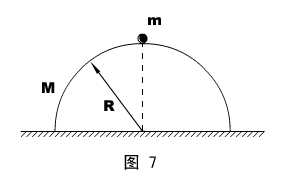
进阶应用：如图7所示，一个质量为M ，半径为R的光滑均质半球，静置于光滑水平桌面上，在球顶有一个质量为m的质点，由静止开始沿球面下滑。试求：质点离开球面以前的轨迹。

解说：质点下滑，半球后退，这个物理情形和上面的双斜面问题十分相似，仔细分析，由于同样满足水平方向动量守恒，故我们介绍的“定式”是适用的。定式解决了水平位移(位置)的问题，竖直坐标则需要从数学的角度想一些办法。

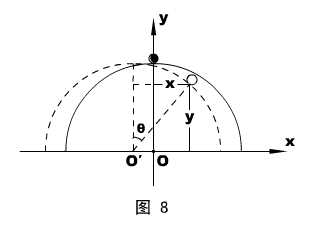
为寻求轨迹方程，我们需要建立一个坐标：以半球球心O为原点，沿质点滑下一侧的水平轴为x坐标、竖直轴为y坐标。

由于质点相对半球总是做圆周运动的(离开球面前)，有必要引入相对运动中半球球心O′的方位角θ来表达质点的瞬时位置，如图8所示。

由“定式”，易得：

x = Rsinθ　　　　　　　　　 ①

而由图知：y = Rcosθ　　　　　　　　 ②

不难看出，①、②两式实际上已经是一个轨迹的参数方程。为了明确轨迹的性质，我们可以将参数θ消掉，使它们成为：

　+ 　= 1

这样，特征就明显了：质点的轨迹是一个长、短半轴分别为R和R的椭圆。

物理情形：在光滑的水平地面上，有一辆车，车内有一个人和N个铅球，系统原来处于静止状态。现车内的人以一定的水平速度将铅球一个一个地向车外抛出，车子和人将获得反冲速度。第一过程，保持每次相对地面抛球速率均为v ，直到将球抛完；第二过程，保持每次相对车子抛球速率均为v ，直到将球抛完。试问：哪一过程使车子获得的速度更大？

模型分析：动量守恒定律必须选取研究对象之外的第三方(或第四、第五方)为参照物，这意味着，本问题不能选车子为参照。一般选地面为参照系，这样对“第二过程”的铅球动量表达，就形成了难点，必须引进相对速度与绝对速度的关系。至于“第一过程”，比较简单：N次抛球和将N个球一次性抛出是完全等效的。

设车和人的质量为M ，每个铅球的质量为m 。由于矢量的方向落在一条直线上，可以假定一个正方向后，将矢量运算化为代数运算。设车速方向为正，且第一过程获得的速度大小为V₁ 第二过程获得的速度大小为V₂ 。

第一过程，由于铅球每次的动量都相同，可将多次抛球看成一次抛出。车子、人和N个球动量守恒。

0 = Nm(-v) + MV₁

得：V₁ = v　　　　　　　　　　　　　 　　　　　①

第二过程，必须逐次考查铅球与车子(人)的作用。

第一个球与(N–1)个球、人、车系统作用，完毕后，设“系统”速度为u₁ 。值得注意的是，根据运动合成法则，铅球对地的速度并不是(-v)，而是(-v + u₁)。它们动量守恒方程为：

0 = m(-v + u₁) +(M +(N-1)m)u₁

得：u₁ =

第二个球与(N -2)个球、人、车系统作用，完毕后，设“系统”速度为u₂ 。它们动量守恒方程为：

(M+(N-1)m)u₁ = m(-v + u₂) +(M+(N-2)m)u₂

得：u₂ = 　+

第三个球与(N -2)个球、人、车系统作用，完毕后，设“系统”速度为u₃ 。铅球对地的速度是(-v + u₃)。它们动量守恒方程为：

(M+(N-2)m)u₂ = m(-v + u₃) +(M+(N-3)m)u₃

得：u₃ = + 　+

以此类推(过程注意：先找u_N和u_N-1关系，再看u_N和v的关系，不要急于化简通分)……，u_N的通式已经可以找出：

V₂ = u_N = 　+ 　+ 　+ … +

即：V₂ = 　　　　　　　　　　　　　　　　②

我们再将①式改写成：

V₁ = 　　　　　　　　　　　　　　　　　　　　①′

不难发现，①′式和②式都有N项，每项的分子都相同，但①′式中每项的分母都比②式中的分母小，所以有：V₁ ＞ V₂ 。

结论：第一过程使车子获得的速度较大。

(学生活动)思考：质量为M的车上，有n个质量均为m的人，它们静止在光滑的水平地面上。现在车上的人以相对车大小恒为v、方向水平向后的初速往车下跳。第一过程，N个人同时跳下；第二过程，N个人依次跳下。试问：哪一次车子获得的速度较大？

解：第二过程结论和上面的模型完全相同，第一过程结论为V₁ = 　。

答：第二过程获得速度大。