
6.①地不能每日都成为集市的根本原因是( D )
A.供交换的商品种类太少
B.为方便各地居民的日常生活
C.各集镇之间交通不便
D.当地居民的购买力不足
文化设施的服务半径是指各项设施所服务的空间距离或时间距离。文化设施的分级与服务半径的确定应考虑两方面的因素﹕一是居民的使用频率﹐二是设施的规模效益。以学校为例﹐中学属于城市级和居住区级项目﹐其服务半径可控制在1000米之内。小学属于综合小区级项目﹐相邻社区的学生以不跨越城市干道为宜﹐服务半径控制在500米以内。读图5回答4-5题
4.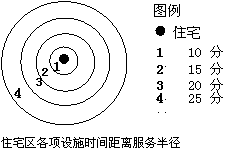 右图6中﹐1-4分别代表不同级别的文化设施﹐
右图6中﹐1-4分别代表不同级别的文化设施﹐
下列排序合理的是
A.1-幼儿园﹐2-中学﹐3-小学﹐4-医院
B.1-幼儿园﹐2-小学﹐3-中学﹐4-医院
C.1-幼儿园﹐2-小学﹐3-医院﹐4-中学
D.1-医院﹐2-幼儿园﹐3-小学﹐4-中学
5.文化设施的布局不受服务半径影响的是
A.大型超市 B.影院 C.网上学校 D.饭店
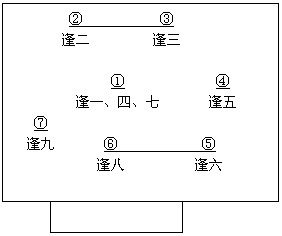 20世纪60年代,我国西部某平原地区在各集镇形成周期性集市。农历每月内,集市逢一、四、七在①地,其余各天分别在周围六个集镇,如左下图所示(初一、十一、廿一为逢一,其余类推)。回答6题。
20世纪60年代,我国西部某平原地区在各集镇形成周期性集市。农历每月内,集市逢一、四、七在①地,其余各天分别在周围六个集镇,如左下图所示(初一、十一、廿一为逢一,其余类推)。回答6题。
新华网沈阳2007年9月22日电:辽宁一业主因采光权被侵犯起诉,获赔2.3万元。为了冬季采光,我国在居住区规划设计标准中,对不同纬度带住宅间的合理间距有明确规定。分析图表(表中H是住宅的高度),回答1-3题。
表1 我国部分城市住宅的日照间距
|
城市 |
冬至日正午太阳高度 |
日照间距 |
|
|
理论 |
实际应用 |
||
|
① |
24°45′ |
2.02H |
1.7H |
|
② |
40°28′ |
1.18H |
1.2H |
|
③ |
35°21′ |
1.41H |
1.1-1.2H |
|
④ |
26°36′ |
1.86H |
1.6-1.7H |
1.表1中的4个城市所处纬度从低到高依次是
A.①②③④ B.①④③② C.②①③④ D.②③④①
2.根据表中信息,在北京修建南北两栋20米高的住宅楼,其理论日照间距约为
A.23米 B.28米 C.37米 D.40米
3.表1反映出我国建筑物的日照间距
A.由南向北逐渐缩小 B.由南向北逐渐扩大
C.由西向东逐渐缩小 D.由西向东逐渐扩大
6、独立事件重复试验:事件A在n次独立重复试验中恰好发生了 次的概率
次的概率 (是二项展开式
(是二项展开式 的第k+1项),其中
的第k+1项),其中 为在一次独立重复试验中事件A发生的概率。如(1)小王通过英语听力测试的概率是
为在一次独立重复试验中事件A发生的概率。如(1)小王通过英语听力测试的概率是 ,他连续测试3次,那么其中恰有1次获得通过的概率是_______(答:
,他连续测试3次,那么其中恰有1次获得通过的概率是_______(答: );(2)冰箱中放有甲、乙两种饮料各5瓶,每次饮用时从中任意取1瓶甲种或乙种饮料,取用甲种或乙种饮料的概率相等,则甲种饮料饮用完毕时乙种饮料还剩下3瓶的概率为__________(答:
);(2)冰箱中放有甲、乙两种饮料各5瓶,每次饮用时从中任意取1瓶甲种或乙种饮料,取用甲种或乙种饮料的概率相等,则甲种饮料饮用完毕时乙种饮料还剩下3瓶的概率为__________(答: )
)
提醒:(1)探求一个事件发生的概率,关键是分清事件的性质。在求解过程中常应用等价转化思想和分解(分类或分步)转化思想处理,把所求的事件:转化为等可能事件的概率(常常采用排列组合的知识);转化为若干个互斥事件中有一个发生的概率;利用对立事件的概率,转化为相互独立事件同时发生的概率;看作某一事件在n次实验中恰有k次发生的概率,但要注意公式的使用条件。(2)事件互斥是事件独立的必要非充分条件,反之,事件对立是事件互斥的充分非必要条件;(3)概率问题的解题规范:①先设事件A=“…”, B=“…”;②列式计算;③作答。
5、独立事件:(事件A、B的发生相互独立,互不影响)P(A•B)=P(A) • P(B) 。提醒:(1)如果事件A、B独立,那么事件A与 、
、 与
与 及事件
及事件 与
与 也都是独立事件;(2)如果事件A、B相互独立,那么事件A、B至少有一个不发生的概率是1-P(A
也都是独立事件;(2)如果事件A、B相互独立,那么事件A、B至少有一个不发生的概率是1-P(A B)=1-P(A)P(B);(3)如果事件A、B相互独立,那么事件A、B至少有一个发生的概率是1-P(
B)=1-P(A)P(B);(3)如果事件A、B相互独立,那么事件A、B至少有一个发生的概率是1-P(

 )=1-P(
)=1-P( )P(
)P( )。如(1)设两个独立事件A和B都不发生的概率为
)。如(1)设两个独立事件A和B都不发生的概率为 ,A发生B不发生的概率与B发生A不发生的概率相同,则事件A发生的概率P(A)是______(答:
,A发生B不发生的概率与B发生A不发生的概率相同,则事件A发生的概率P(A)是______(答: );(2)某同学参加科普知识竞赛,需回答三个问题,竞赛规则规定:答对第一、二、三个问题分别得100分、100分、200分,答错得0分,假设这位同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响,则这名同学得300分的概率为_____________;这名同学至少得300分的概率为_____________(答:0.228;0.564);(3)袋中有红、黄、绿色球各一个,每次任取一个,有放回地抽取三次,球的颜色全相同的概率是________(答:
);(2)某同学参加科普知识竞赛,需回答三个问题,竞赛规则规定:答对第一、二、三个问题分别得100分、100分、200分,答错得0分,假设这位同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响,则这名同学得300分的概率为_____________;这名同学至少得300分的概率为_____________(答:0.228;0.564);(3)袋中有红、黄、绿色球各一个,每次任取一个,有放回地抽取三次,球的颜色全相同的概率是________(答: );(4)一项“过关游戏”规则规定:在第
);(4)一项“过关游戏”规则规定:在第 关要抛掷一颗骰子
关要抛掷一颗骰子 次,如果这
次,如果这 次抛掷所出现的点数之和大于
次抛掷所出现的点数之和大于 ,则算过关,那么,连过前二关的概率是________(答:
,则算过关,那么,连过前二关的概率是________(答: );(5)有甲、乙两口袋,甲袋中有六张卡片,其中一张写有0,两张写有1,三张写有2;乙袋中有七张卡片,四张写有0,一张写有1,两张写有2,从甲袋中取一张卡片,乙袋中取两张卡片。设取出的三张卡片的数字乘积的可能值为
);(5)有甲、乙两口袋,甲袋中有六张卡片,其中一张写有0,两张写有1,三张写有2;乙袋中有七张卡片,四张写有0,一张写有1,两张写有2,从甲袋中取一张卡片,乙袋中取两张卡片。设取出的三张卡片的数字乘积的可能值为 且
且 ,其相应的概率记为
,其相应的概率记为 ,则
,则 的值为_____________(答:
的值为_____________(答: );(6)平面上有两个质点A、B分别位于(0,0)、(2,2)点,在某一时刻同时开始每隔1秒钟向上下左右四个方向中的任何一个方向移动1个单位,已知质点A向左、右移动的概率都是
);(6)平面上有两个质点A、B分别位于(0,0)、(2,2)点,在某一时刻同时开始每隔1秒钟向上下左右四个方向中的任何一个方向移动1个单位,已知质点A向左、右移动的概率都是 ,向上、下移动的概率分别是
,向上、下移动的概率分别是 和p,质点B向四个方向中的任何一个方向移动的概率都是q。①求p和q的值;②试判断最少需要几秒钟,A、B能同时到达D(1,2)点?并求出在最短时间内同时到达的概率. (答:①
和p,质点B向四个方向中的任何一个方向移动的概率都是q。①求p和q的值;②试判断最少需要几秒钟,A、B能同时到达D(1,2)点?并求出在最短时间内同时到达的概率. (答:① ;②3秒;
;②3秒; )
)
4、对立事件:(A、B对立,即事件A、B不可能同时发生,但A、B中必然有一个发生)。计算公式是:P(A)+ P(B)=1;P( )=1-P(A);
)=1-P(A);
3、互斥事件:(A、B互斥,即事件A、B不可能同时发生)。计算公式:P(A+B)=P(A)+P(B)。如(1)有A、B两个口袋,A袋中有4个白球和2个黑球,B袋中有3个白球和4个黑球,从A、B袋中各取两个球交换后,求A袋中仍装有4个白球的概率。(答: );(2)甲、乙两个人轮流射击,先命中者为胜,最多各打5发,已知他们的命中率分别为0.3和0.4,甲先射,则甲获胜的概率是(0.425=0.013,结果保留两位小数)______(答:0.51);(3)有一个公用电话亭,在观察使用这个电话的人的流量时,设在某一时刻,有n个人正在使用电话或等待使用的概率为P(n),且P(n)与时刻t无关,统计得到
);(2)甲、乙两个人轮流射击,先命中者为胜,最多各打5发,已知他们的命中率分别为0.3和0.4,甲先射,则甲获胜的概率是(0.425=0.013,结果保留两位小数)______(答:0.51);(3)有一个公用电话亭,在观察使用这个电话的人的流量时,设在某一时刻,有n个人正在使用电话或等待使用的概率为P(n),且P(n)与时刻t无关,统计得到  ,那么在某一时刻,这个公用电话亭里一个人也没有的概率P(0)的值是 (答:
,那么在某一时刻,这个公用电话亭里一个人也没有的概率P(0)的值是 (答: )
)
2.等可能事件的概率(古典概率): P(A)= 。理解这里m、n的意义。如(1)将数字1、2、3、4填入编号为1、2、3、4的四个方格中,每格填一个数字,则每个方格的标号与所填数字均不相同的概率是______(答:
。理解这里m、n的意义。如(1)将数字1、2、3、4填入编号为1、2、3、4的四个方格中,每格填一个数字,则每个方格的标号与所填数字均不相同的概率是______(答: );(2)设10件产品中有4件次品,6件正品,求下列事件的概率:①从中任取2件都是次品;②从中任取5件恰有2件次品;③从中有放回地任取3件至少有2件次品;④从中依次取5件恰有2件次品。(答:①
);(2)设10件产品中有4件次品,6件正品,求下列事件的概率:①从中任取2件都是次品;②从中任取5件恰有2件次品;③从中有放回地任取3件至少有2件次品;④从中依次取5件恰有2件次品。(答:① ;②
;② ;③
;③ ;④
;④ )
) 
1.随机事件 的概率
的概率 ,其中当
,其中当 时称为必然事件;当
时称为必然事件;当 时称为不可能事件P(A)=0;
时称为不可能事件P(A)=0; 
6.将VLNO和NO2的混合气体通过水吸收后,得到amL无色气体A。将此无色气体A与等体积O2混合,再通过水充分吸收后,收集到5mL无色气体B。试回答:
(1)A气体是__________________,B气体是_________________________。
(2)A气体的体积是______________________mL
(3)V值的取值范围是____________________。
答案:(1)A是NO;B是O2。(2)20mL。(3)20<V<60。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com