
3.蛋白质代谢与人体健康
人体每天都必须摄入足够的 。 含氨基酸种类较齐全,有些 缺某些必需氨基酸。如果人的食物种类过于单一(如只吃大米),体内就会由于缺乏某些
而导致蛋白质合成受阻,出现营养不良,故要合理选择和搭配食物。
命题研究
|
考点搜索 |
出题方向 |
解题策略 |
|
糖类代谢。 |
考查能否准确记忆血糖的来源和去路。命题时一般综合考查血糖的调节。 |
解题的关键是必须理清糖类代谢的过程。因命题一般都是结合代谢过程示意图,故需要加强识图能力和图文转换能力的训练。 |
|
脂质代谢。 |
考查食物中的脂肪经过消化吸收后,发生的四种变化。 |
解题的关键是必须把握脂质代谢的过程。结合代谢过程示意图,分析脂质代谢的中物质的变化。 |
|
蛋白质代谢。(2000年、2004年) |
考查能否准确记忆蛋白质代谢中氨基酸的来源和去路及对转氨基作用和脱氨基作用的理解。 |
解题的关键是必须理解和掌握蛋白质代谢的过程,把握代谢中物质的去向和转变。 |
|
三大营养物质代谢的关系。(2003年、2004年) |
体内三大营养物质的相互转化是命题的热点。 |
解题时把握在生物体的同一个细胞内,糖类代谢、脂质代谢、蛋白质代谢三大营养物质的代谢是同时进行的,它们之间的过程既有相互联系的地方,又有不同的地方,只有建立知识相互联系的网络,才能准确回答。另外还需要注意三大营养物质相互转化的条件。 |
|
三大营养物质代谢与人体健康的关系。 |
要求分析低血糖、糖尿病、高血脂、脂肪肝、肥胖、某些氨基酸缺乏性营养不良症的原因并明确防治措施。 |
此类卫生保健问题需要结合物质代谢的过程,同时复习时需加强记忆。 |
提分关键
2.脂质代谢与人体健康
 肥胖:一般情况下,如果一个人摄入的供能物质(如糖类)多,而消耗的供能物质少,不但来自食物中的 可以储存在体内,而且体内过多的
也可以转变成脂肪储存于体内,这样就导致了肥胖。这种肥胖可以通过
肥胖:一般情况下,如果一个人摄入的供能物质(如糖类)多,而消耗的供能物质少,不但来自食物中的 可以储存在体内,而且体内过多的
也可以转变成脂肪储存于体内,这样就导致了肥胖。这种肥胖可以通过
措施来治疗。
脂肪肝、肝硬化:肝脏功能不好或 等的合成减少时,脂肪合成 受阻,脂肪不能顺利运出,在肝脏中堆积,形成 。长期发展,会使肝细胞坏死,结缔组织增生,最终造成 。合理 ,适当的
,并注意吃一些含 较多的食物,是防治脂肪肝的有效措施。
1.糖类代谢与人体健康
正常人的血糖含量是 。一般情况下,血糖的 和 能保持相对平衡,血糖含量就会保持相对稳定。
 血糖含量降低至 会出现低血糖早期症状,
即可恢复。
血糖含量降低至 会出现低血糖早期症状,
即可恢复。
低血糖
血糖含量低于 会出现低血糖晚期症状, 即可缓解。
三大营养物质代谢之间是可以转化的,它们之间的关系如下:

注:图中的虚线箭头指 。
3.蛋白质代谢的主要途径
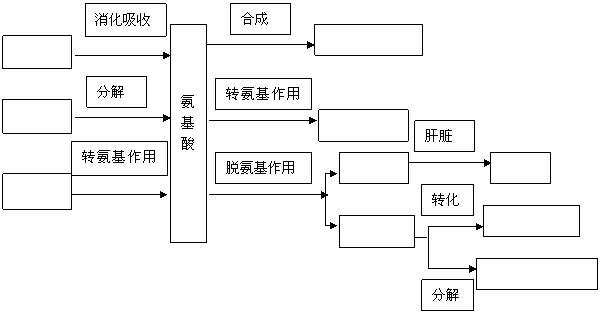
*通过转氨基作用,把 转移给其他化合物,可以形成新的氨基酸。如:
GPT
 + 丙酮酸 + 另一种酮酸
+ 丙酮酸 + 另一种酮酸
 非必需氨基酸:
氨基酸叫非必需氨基酸。例如,丙氨酸、甘氨酸。
非必需氨基酸:
氨基酸叫非必需氨基酸。例如,丙氨酸、甘氨酸。
人体必需氨基酸:不能在人体内合成,只能 的氨基酸,人体必需
氨基酸共8种
。
2.脂质代谢的主要途径

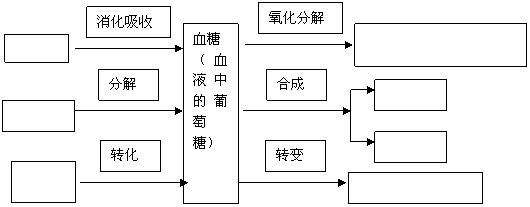
1.糖类代谢的主要途径
3.(2009年上海卷理)若复数 z 满足z (1+i) =1-i (I是虚数单位),则其共轭复数 =__________________ .
=__________________ .
[答案]i
. 

[解析]设z=a+bi,则(a+bi )(1+i) =1-i,即a-b+(a+b)i=1-i,由 ,解得a=0,b=-1,所以z=-i,
,解得a=0,b=-1,所以z=-i, =i
=i
2.(2009福建卷文)复数 的实部是 -1 。
的实部是 -1 。
解析  =-1-I,所以实部是-1。
=-1-I,所以实部是-1。
1.(2009江苏卷)若复数 其中
其中 是虚数单位,则复数
是虚数单位,则复数 的实部为 。
的实部为 。
[解析]考查复数的减法、乘法运算,以及实部的概念。 -20
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com