8．[2010·重庆二诊]已知直线过点和点，则直线的斜率的最大值为(　 )

A.　　　　　　 B.　　　　　　　 C.　　　　　　　 D.

[答案]D

[解析]∵动点的轨迹方程为圆：，∴当直线与圆相切时，斜率取得最值，此时，，故选D.

7．[2010·曲靖一中届高考冲刺卷数学(七)理科]已知曲线 ，则过点P(1,0)的曲线C的切线斜率为(　　 )

　　 A. 2　　　　　　 B.4　　　　　　 C.0或2　　　　　 D. 0或4

[答案]A

[解析]k=y'|_x=1=2×1=2，故选A。

6. [2010•安徽理数]动点在圆上绕坐标原点沿逆时针方向匀速旋转，12秒旋转一周。已知时间时，点的坐标是，则当时，动点的纵坐标关于(单位：秒)的函数的单调递增区间是(　 )

A、　　　　　　　　 B、　　　　　　　　　　　 C、　　　　　　　　 D、和

[答案]D

[解析]画出图形，设动点A与轴正方向夹角为，则时，每秒钟旋转，在上，在上，动点的纵坐标关于都是单调递增的。

[方法技巧]由动点在圆上绕坐标原点沿逆时针方向匀速旋转，可知与三角函数的定义类似，由12秒旋转一周能求每秒钟所转的弧度，画出单位圆，很容易看出，当t在变化时，点的纵坐标关于(单位：秒)的函数的单调性的变化，从而得单调递增区间.

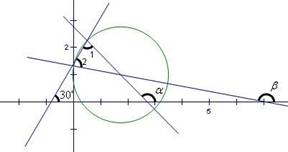
5. [2010•全国卷1理数]已知圆O的半径为1，PA、PB为该圆的两条切线，A、B为两切点，那么的最小值为(　 )

A. 　　　B.　 C. 　D.

[答案]D

4. [2010•重庆理数]直线y=与圆心为D的圆交与A、B两点，则直线AD与BD的倾斜角之和为(　 )

A.　 　　　　　　　B.　 　　　　　C.　 　　　　　D.

[答案]C

[解析]数形结合

由圆的性质可知

故

3. [2010•重庆文数]若直线与曲线()有两个不同的公共点，则实数的取值范围为(　 )

A. 　　　　　　　　　　　　　　　　B.

C.　　　　　　　 D.

[答案]D

[解析]化为普通方程，表示圆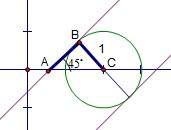，因为直线与圆有两个不同的交点，所以解得

法2：利用数形结合进行分析得

同理分析，可知

2.[2010•安徽文数]过点(1，0)且与直线x-2y-2=0平行的直线方程是(　 )

A.x-2y-1=0　　　　 B.x-2y+1=0　　 C.2x+y-2=0　　　　 D.x+2y-1=0

[答案]A

[解析]设直线方程为，又经过，故，所求方程为.

[方法技巧]因为所求直线与与直线x-2y-2=0平行，所以设平行直线系方程为，代入此直线所过的点的坐标，得参数值，进而得直线方程.也可以用验证法，判断四个选项中方程哪一个过点(1，0)且与直线x-2y-2=0平行.

1.[2010•江西理数]直线与圆相交于M,N两点，若，则k的取值范围是(　 )

A. 　　　　　B. 　C. 　　　　D.

[答案]A

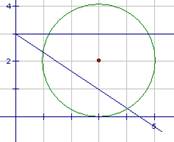[解析]考查直线与圆的位置关系、点到直线距离公式，重点考察数形结合的运用.

解法1：圆心的坐标为(3.，2)，且圆与y轴相切.当，由点到直线距离公式，解得；

解法2：数形结合，如图由垂径定理得夹在两直线之间即可， 不取，排除B，考虑区间不对称，排除C，利用斜率估值，选A