10．非零不共线向量、，且2＝x+y，若＝λ (λ∈R)，则点Q(x，y)的轨迹方程是　　　　　　　　　　　　　　　　　　　　　　 (　)

A．x+y－2＝0　 　　　　　　　　　　　　　B．2x+y－1＝0

C．x+2y－2＝0 　　　　　　　　　　　　　D．2x+y－2＝0

解析：＝λ，得－＝λ(－)，

即＝(1+λ) －λ.

又2＝x+y，

∴消去λ得x+y＝2.

答案：A

9.已知平面上不共线的四点O、A、B、C.若－4+3＝0，则＝________

A.　 　　　B.　　　　 C．2 　　　　D．3

解析：∵－4+3＝0，∴(－)－3+3＝0，即－＝3(－)，∴＝3，∴＝3.

答案：D

8．设e₁、e₂是平面内一组基向量，且a＝e₁+2e₁、b＝－e₁+e₂，则向量e₁+e₂可以表示另一组基向量a、b的线性组合，则e₁+e₂＝________a+________b.

解析：设e₁+e₂＝xa+yb，

即e₁+e₂＝(x－y)e₁+(2x+y)e₂.

∴∴x＝，y＝－.

答案：　－

7.(2009·湖南高考)对于非零向量a、b，“a+b＝0”是“a∥b”的　　　　　　　 (　)

A．充分不必要条件　 　　　　　B．必要不充分条件

C．充分必要条件　　　　　 　D．既不充分也不必要条件

解析：由a+b＝0知道a与b互为相反向量，从而a∥b，充分性成立. 由a∥b知a＝λb.λ≠－1时，a+b≠0，∴必要性不成立．

答案：A

6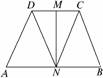．如图，若四边形ABCD是一个等腰梯形，AB∥DC，M、

N分别是DC，AB的中点，已知＝a，＝b，＝

c，试用a，b，c表示，，+.

解：＝++＝－a+b+c.

∵＝++，

＝++，

∴2＝+++++＝+＝－+ ＝－b－(－a+b+c)＝a－2b－c，

∴＝a－b－c.

+＝+++

＝2＝a－2b－c.

5．(2009·安徽高考)在平行四边形ABCD中，E和F分别是边CD和BC的中点．若＝λ+μ，其中，λ，μ∈R，则λ+μ＝________.

解析：如图，∵ABCD为▱，且E、F分别为CD、BC中点．

∴＝+

＝(－)+(－)

＝(+)－(+)

＝(+)－，

∴＝(+)，

∴λ＝μ＝，∴λ+μ＝.

答案：

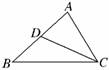
4．如图所示，D是△ABC的边AB的中点，则向量＝　　　　　　　 (　)

A．－+ 　　　　　　B．－－

C．－　　　 　　　 D. +

解析：＝+＝－+.

答案：A

3.若A、B、C、D是平面内任意四点，给出下列式子：①+＝+；②+＝+；③－＝+.其中正确的有　　　　　 (　)

A．0个　 　　　B．1个　　　　　 C．2个 　　　　D．3个

解析：①式的等价式是－＝－，左边＝+，右边＝+，不一定相等；

②式的等价式是－＝－，+＝+＝成立；

③式的等价式是－＝+，＝成立．

答案：C

2．下列四个命题，其中正确的个数有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

①对于实数m和向量a，b，恒有m(a－b)＝ma－mb

②对于实数m，n和向量a，恒有(m－n)a＝ma－na

③若ma＝mb(m∈R)，则有a＝b

④若ma＝na(m，n∈R，a≠0)，则有m＝n

A．1个　　 B．2个　　　　 C．3个 　　　　　D．4个

解析：只有③不正确，∵a≠b，m＝0时，ma＝mb也成立，其余①②④均成立．

答案：C

1.给出下列六个命题：

①两个向量相等，则它们的起点相同，终点相同；

②若|a|＝|b|，则a＝b；

③若＝，则四边形ABCD为平行四边形；

④在▱ABCD中，一定有＝；

⑤若m＝n，n＝p，则m＝p；

⑥若a∥b，b∥c，则a∥c，

其中不正确的个数是　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．2　　 　B．3 　　　　C．4　 　D．5

解析：两向量起点相同，终点相同，则两向量相等；但两相等向量，不一定有相同的起点和终点，故①不正确．|a|＝|b|，由于a与b方向不确定，所以a，b不一定相等，故②不正确．零向量与任一向量平行，故a∥b，b∥c时，若b＝0，则a与c不一定平行，故⑥不正确．正确的是③④⑤.

答案：B