8.(2010·温州模拟)下列命题中，真命题是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.∃x∈R，使得sinx+cosx＝2

B.∀x∈(0，π)，有sinx＞cosx

C.∃x∈R，使得x²+x＝－2

D.∀x∈(0，+∞)，有e^x＞1+x

解析：∵sinx+cosx＝sin(x+)≤，故A错；

当0＜x＜时，cosx＞sinx，故B错；

∵方程x²+x+2＝0无解，故C错误；

令f(x)＝e^x－x－1，则f′(x)＝e^x－1

又∵x∈(0，+∞)，∴f′(x)＝e^x－x－1在(0，+∞)上为增函数，∴f(x)＞f(0)＝0，

即e^x＞1+x，故D正确.

答案：D

7.同时满足①M⊆{1,2,3,4,5}；②若a∈M，则6－a∈M的非空集合M有　　　　　 (　)

A.16个　 　　B.15个　　 C.7个　 　　　D.6个

解析：∵1+5＝2+4＝3+3＝6，∴集合M可能为单元素集：{3}；二元素集：{1,5}，{2,4}；三元素集：{1,3,5}，{2,3，4}；四元素集：{1,2,4,5}；五元素集：{1,2,3,4,5}.共7个.

答案：C

6.下列说法错误的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.命题：“已知f(x)是R上的增函数，若a+b≥0，则f(a)+f(b)≥f(－a)+f(－b)”的逆否命题为真命题

B.“x＞1”是“|x|＞1”的充分不必要条件

C.若p且q为假命题，则p、q均为假命题

D.命题p：“∃x∈R，使得x²+x+1＜0”，则　 p：“∀x∈R，均有x²+x+1≥0”

解析：A中∵a+b≥0，∴a≥－b.

又函数f(x)是R上的增函数，∴f(a)≥f(－b)，①

同理可得，f(b)≥f(－a)，②

由①+②，得f(a)+f(b)≥f(－a)+f(－b)，即原命题为真命题.

又原命题与其逆否命题是等价命题，

∴逆否命题为真.

若p且q为假命题，则p、q中至少有一个是假命题，所以C错误.

答案：C

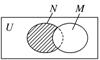
5.(文)设全集U是实数集R，M＝{x|x²＞4}，N＝{x|1＜x＜3}，

则图中阴影部分表示的集合是　　　　　　　　　 (　)

A.{x|－2≤x＜1}　　　　 B.{x|1＜x≤2}

C.{x|－2≤x≤2}　　　　 D.{x|x＜2}

解析：阴影部分表示的集合为N∩∁_UM＝{x|1＜x≤2}.

答案：B

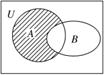(理)设全集U＝R，集合A＝{x|2^x(x－2)＜1}，B＝{x|y＝ln(1－x)}，

则图中阴影部分表示的集合为　　　　　　　　　　 (　)

A.{x|x≥1}　　　　　 B.{x|x≤1}

C.{x|0＜x≤1} 　　　　 D.{x|1≤x＜2}

解析：由2^x(x－2)＜1得x(x－2)＜0，故集合A＝{x|0＜x＜2}，由1－x＞0得x＜1，故B＝{x|x＜1}，所以A∩B＝{x|0＜x＜1}，所以∁_A(A∩B)＝{x|1≤x＜2}，即图中阴影部分表示的集合为{x|1≤x＜2}.

答案：D

4.(2009·浙江高考)已知a，b是实数，则“a>0且b>0”是“a+b>0且ab>0”的　　 (　)

A.充分而不必要条件　　　　 B.必要而不充分条件

C.充分必要条件　　　　　 D.既不充分也不必要条件

解析：a>0，b>0时显然有a+b>0且ab>0，充分性成立；反之，若a+b>0且ab>0，则a，b同号且同正，即a>0，b>0.必要性成立.

答案：C

3.命题“若a＞b，则a－1＞b－1”的否命题是　　　　　　　　　　　　　　　 (　)

A.若a＞b，则a－1≤b－1　　 　B.若a≥b，则a－1＜b－1

C.若a≤b，则a－1≤b－1　　　 D.若a＜b，则a－1＜b－1

解析：即命题“若p，则q”的否命题是“若 p，则　 q”.

答案：C

2.(2009·全国卷Ⅱ)已知全集U＝{1,2,3,4,5,6,7,8}，M＝{1,3,5,7}，N＝{5,6,7}，则∁_U(M∪N)＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.{5,7}　 　　B.{2,4}　　 C.{2,4,8}　 　　D.{1,3,5,6,7}

解析：M∪N＝{1,3,5,6,7}，∴∁_U(M∪N)＝{2,4,8}.

答案：C

1.若集合M＝{x∈R|－3＜x＜1}，N＝{x∈Z|－1≤x≤2}，则M∩N＝　　　　　 (　)

A.{0}　　B.{－1,0}　　　 C.{－1,0,1}　 　　　D.{－2，－1,0,1,2}

解析：因为集合N＝{－1,0,1,2}，所以M∩N＝{－1,0}.

答案：B

在具体解题时往往找不出夹角，关键是不能求斜线在平面内的射影，通过练习，使学生在不同的视图中能较熟练地找出射影

在正方体ABCD-A₁B₁C₁D₁中，E、F分别是AA₁、A₁D₁的中点，求：

(1)D₁B₁与面AC所成角的余弦值；

(2)EF与面A₁C₁所成的角；

(3)EF与面AC所成的角．

解：(1)设正方体的边长为a，则在中，.

∴.

(2)45°．(3)45°．