8、(浙江理4)直线x－2y+1＝0关于直线x＝1对称的直线方程是

(A)x+2y－1＝0　 　　　　(B)2 x+y－1＝0

(C)2 x+y－3＝0　 　　　(D) x+2y－3＝0

[答案]：D

[分析]：解法一(利用相关点法)设所求直线上任一点(x,y),则它关于对称点为(2-x,y)在直线上,化简得故选答案D.

解法二根据直线关于直线对称的直线斜率是互为相反数得答案A或D,再根据两直线交点在直线选答案D.

7、(浙江理4文5)要在边长为16米的正方形草坪上安装喷水龙头，使整个草坪

　都能喷洒到水．假设每个喷水龙头的喷洒范围都是半径为6米

的圆面，则需安装这种喷水龙头的个数最少是(　)

A．　　　　　 B．　　　　　 C．　　　　　 D．

[答案]B

[分析]：因为龙头的喷洒面积为36π，

正方形面积为256,故至少三个龙头。

由于，故三个龙头肯定不能

保证整个草坪能喷洒到水。当用四个

龙头时，可将正方形均分四个小正方形，

同时将四个龙头分别放在它们的中心，

由于，故可以保证

整个草坪能喷洒到水。

6、(浙江理3)直线关于直线对称的直线方程是(　)

A．　　　　　　　　　　 B．

C．　　　　　　　　　　 D．

[答案]：D

[分析]：解法一(利用相关点法)设所求直线上任一点(x,y),则它关于对称点为(2-x,y)

在直线上,化简得故选答案D.

解法二：根据直线关于直线对称的直线斜率是互为相反数得答案A或D,

再根据两直线交点在直线选答案D.

5、(湖北文8)由直线y=x+1上的一点向圆(x-3)²+y²=1引切线，则切线长的最小值为 A.1　　　　　　　　　　　 　 B.2　　　　　　　　　　　　　 C.　　　　　　　 D.3

答案：选C

解析：切线长的最小值是当直线y=x+1上的点与圆心距离最小时取得，圆心(3，0)到直线的距离为d=，圆的半径为1，故切线长的最小值为，选C

4、(湖北理10)已知直线(是非零常数)与圆有公共点，且公共点的横坐标和纵坐标均为整数，那么这样的直线共有(　　 )

A．60条　　　　　　　　　 B．66条　　　　　　　 C．72条　　　　　　　 D．78条

答案：选A

解析：可知直线的横、纵截距都不为零，即与坐标轴不垂直，不过坐标原点，而圆

上的整数点共有12个，分别为，

，前8个点中，过任意一点的圆的切线满足，有8条；12个点中过任意两点，构成条直线，其中有4条直线垂直轴，有4条直线垂直轴，还有6条过原点(圆上点的对称性)，故满足题设的直线有52条。综上可知满足题设的直线共有条，选A

3、(上海文13)圆关于直线对称的圆的方程是(　)

　　 A．　　　　　　　　 B．

　　 C．　　 　　　　　　　 D．

[答案]C

[解析]圆，圆心(1，0)，半径，关于直线对称的圆半径不变，排除A、B，两圆圆心连线段的中点在直线上，C中圆的圆心为(－3，2)，验证适合，故选C。

2、(安徽文5)若圆的圆心到直线的距离为,则a的值为

(A)-2或2　　　　　　　　　 (B)　　　　 (C)2或0　　　　　　　 (D)-2或0

解析：若圆的圆心(1，2)到直线的距离为，∴ ，∴ a=2或0，选C。

1、．与直线和曲线都相切的

半径最小的圆的标准方程是　　　　 ．

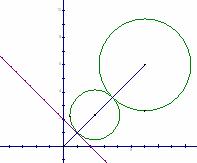[答案]:.

[分析]：曲线化为，其圆心到直线的距离为所求的最小圆的圆心在直线上，其到直线的距离为，圆心坐标为标准方程为。

35．(上海春)已知圆和直线. 若圆与直线没有公共点，则的取值范围是　　　　　　　　　 .

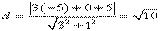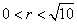解：由题意知，圆心(-5,0) 到直线 l:3x+y+5=0 的距离 d 必须小于圆的半径 r ．因为 ，所以 ．从而应填 ．

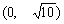2007年高考数学试题分类详解

直线与圆

34．(重庆卷)已知变量，满足约束条件。若目标函数(其中)仅在点处取得最大值，则的取值范围为　　　 　　　　。

解：画出可行域如图所示，其中B(3，0)，

C(1，1)，D(0，1)，若目标函数取

得最大值，必在B，C，D三点处取得，故有

3a>a+1且3a>1，解得a>