
3.吸收 吸收方式:
呼吸作用提供
影响吸收的因素
细胞膜上 的
2.矿质元素的概念:除 之外,主要是由 从 中吸收的元素。目前,科学家确定植物必需的矿质元素有 种。
吸收状态:
大量元素: 等9种;
1.植物必需的元素
微量元素: 等8种。
5.合理灌溉
应用:根据植物的需水规律, 灌溉。
4.利用和散失
95%-99%的水分通过 作用散失,所产生的拉力,是
的重要动力。
 原理:不同植物的 不同,同一植物在
亦不相同。
原理:不同植物的 不同,同一植物在
亦不相同。
3.运输:根吸收的水分,通过根部的 输送到茎,再由茎输送到叶。
 1%-5%的水分用于 作用和 作用等生命活动
1%-5%的水分用于 作用和 作用等生命活动
2.渗透吸水
(主要的
吸水方式) 吸水:外界溶液浓度 细胞液浓度
原理 失水:外界溶液浓度 细胞液浓度
验证: 实验
举例: 细胞
1.概念:水分代谢是指水分的 、 、 和 。
 主要吸水器官和部位:
主要吸水器官和部位:
细胞壁:
细胞结构特点 原生质层:
浓度差 构成一个渗透系统
细胞液 外界溶液
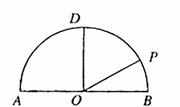
3.(湖北卷19)(本小题满分13分)
如图,在以点 为圆心,
为圆心, 为直径的半圆
为直径的半圆 中,
中, ,
, 是半圆弧上一点,
是半圆弧上一点,
 ,曲线
,曲线 是满足
是满足 为定值的动点
为定值的动点 的轨迹,且曲线
的轨迹,且曲线 过点
过点 .
.
(Ⅰ)建立适当的平面直角坐标系,求曲线 的方程;
的方程;
(Ⅱ)设过点 的直线l与曲线
的直线l与曲线 相交于不同的两点
相交于不同的两点 、
、 .
.
若△ 的面积不小于
的面积不小于 ,求直线
,求直线 斜率的取值范围.
斜率的取值范围.
本小题主要考查直线、圆和双曲线等平面解析几何的基础知识,考查轨迹方程的求法、不等式的解法以及综合解题能力.(满分13分)
(Ⅰ)解法1:以O为原点,AB、OD所在直线分别为x轴、y轴,建立平面直角坐标系,则A(-2,0),B(2,0),D(0,2),P( ),依题意得
),依题意得
|MA|-|MB|=|PA|-|PB|= <|AB|=4.
<|AB|=4.
∴曲线C是以原点为中心,A、B为焦点的双曲线.
设实平轴长为a,虚半轴长为b,半焦距为c,
则c=2,2a=2 ,∴a2=2,b2=c2-a2=2.
,∴a2=2,b2=c2-a2=2.
∴曲线C的方程为 .
.
解法2:同解法1建立平面直角坐标系,则依题意可得|MA|-|MB|=|PA|-|PB|<
|AB|=4.
∴曲线C是以原点为中心,A、B为焦点的双曲线.
设双曲线的方程为 >0,b>0).
>0,b>0).
则由 解得a2=b2=2,
解得a2=b2=2,
∴曲线C的方程为
(Ⅱ)解法1:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理得(1-k2)x2-4kx-6=0.
∵直线l与双曲线C相交于不同的两点E、F,
∴ 


∴k∈(- ,-1)∪(-1,1)∪(1,
,-1)∪(-1,1)∪(1, ).
).
设E(x,y),F(x2,y2),则由①式得x1+x2= ,于是
,于是
|EF|=
=
而原点O到直线l的距离d= ,
,
∴S△DEF=
若△OEF面积不小于2 ,即S△OEF
,即S△OEF ,则有
,则有
 ③
③
综合②、③知,直线l的斜率的取值范围为[- ,-1]∪(1-,1) ∪(1,
,-1]∪(1-,1) ∪(1,  ).
).
解法2:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0.
∵直线l与双曲线C相交于不同的两点E、F,
∴ 


∴k∈(- ,-1)∪(-1,1)∪(1,
,-1)∪(-1,1)∪(1, ).
).
设E(x1,y1),F(x2,y2),则由①式得
|x1-x2|= ③
③
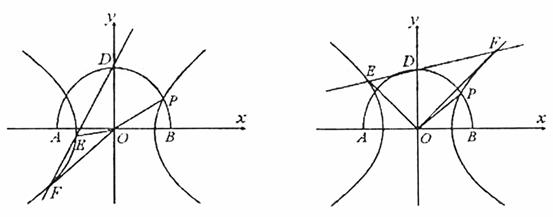
当E、F在同一去上时(如图1所示),
S△OEF=
当E、F在不同支上时(如图2所示).
 S△ODE=
S△ODE=
综上得S△OEF= 于是
于是
由|OD|=2及③式,得S△OEF=
若△OEF面积不小于2
 ④
④
综合②、④知,直线l的斜率的取值范围为[- ,-1]∪(-1,1)∪(1,
,-1]∪(-1,1)∪(1, ).
).
2.(江苏卷18)设平面直角坐标系 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
(Ⅰ)求实数b 的取值范围;
(Ⅱ)求圆C 的方程;
(Ⅲ)问圆C 是否经过某定点(其坐标与b 无关)?请证明你的结论.
[解析]本小题主要考查二次函数图象与性质、圆的方程的求法.
(Ⅰ)令 =0,得抛物线与
=0,得抛物线与 轴交点是(0,b);
轴交点是(0,b);
令 ,由题意b≠0 且Δ>0,解得b<1 且b≠0.
,由题意b≠0 且Δ>0,解得b<1 且b≠0.
(Ⅱ)设所求圆的一般方程为

令 =0 得
=0 得 这与
这与 =0 是同一个方程,故D=2,F=
=0 是同一个方程,故D=2,F= .
.
令 =0 得
=0 得 =0,此方程有一个根为b,代入得出E=―b―1.
=0,此方程有一个根为b,代入得出E=―b―1.
所以圆C 的方程为 .
.
(Ⅲ)圆C 必过定点(0,1)和(-2,1).
证明如下:将(0,1)代入圆C 的方程,得左边=0 +1
+1 +2×0-(b+1)+b=0,右边=0,
+2×0-(b+1)+b=0,右边=0,
所以圆C 必过定点(0,1).
同理可证圆C 必过定点(-2,1).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com