4．祖暅原理的引入--利用“小试验”验证以上猜想：

(1)取一叠裁切相同的纸张堆放在水平桌面上，然后用手推一下以改变其形状．

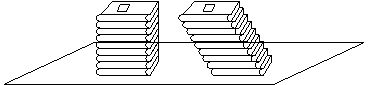
启发思考：

1)　　　 推斜以后体积变化了吗？(几何体所占空间的大小不变)

2)　　　 推斜前后的两个几何体(前为长方体，后为平行六面体)还有什么共同之处？(高度没有改变，每页纸张的顺序和面积也没有改变)

3)　　　 这种共同之处是不是就是两个几何体体积相等的条件呢？

(2)用一摞不同的书，推移成各种形状，继续探讨结论是否正确．(不一定是棱柱)

(3)由学生总结归纳出祖暅原理的大致内容．

3．从平面到空间的类比猜想：(利用几何画板的动态演示)

(1)等底等高的长方形和平行四边形的面积有何关系？

(2)等底等高的三角形的面积有何关系？

(3)等底等高的梯形的面积有何关系？

结论：根据面积公式我们可以得到面积均相等．初中我们学过的面积公式的推导是因为任意平面多边形(直边形)都可以用割补的方法转化为长方形的面积得到．在利用几何画板动态演示的过程中，我们发现，用平行于底边的任意直线截两个平面图形得到的截线长度总相等．

启发思考：这是否可以成为两个平面图形面积相等的条件呢？

继续探究：线是由无穷多个点构成的，面是由无穷多条线构成的，立体是由无穷多个平面构成的．因此我们可以得到：夹在两条平行直线之间的两个平面图形，被平行于这两条直线的任意直线所截，如果所得的两条截线长度相等，那么，这两个平面图形的面积相等．

猜想：类比到两个空间图形体积相等的条件有什么相似的结论呢？用平行于底面的任意平面截两个空间图形得到的截面面积总相等，则这两个空间图形的体积相等．

2．进一步考虑正方体、长方体的体积公式的来龙去脉：

(1)请学生谈谈对体积的理解，并小结：几何体占空间部分的大小叫做它的体积．

(2)　　 提问：体积是如何度量的？(类比长度的度量和面积的度量)

学生讨论后小结：

1)我们在度量长度时，有一个标准，比如说，1米，1厘米等；将一段线段用1厘米来截，看这个线段是1厘米的多少个倍数，就是这个线段有多少厘米．5倍就是5厘米，1.5倍就是1.5厘米．

2)在度量面积时，也有一个标准，比如说1平方米即边长为1米的正方形作为1个单位面积，去度量平面图形的面积．因此，我们容易得到正方形的面积等于棱长的平方，长方形的面积等于底乘以高．因为任意多边形都可以分割成若干个三角形，三角形可以补成平行四边形，平行四边形可以割补成长方形，所以任意平面多边形的面积都可以度量．(直边形)

3)在体积中，我们也要先选定一个单位，用来度量体积，然后求出几何体是单位体积的多少倍，多少个倍数就是几何体的体积数值．通常把棱长等于单位长度的正方体所占空间的大小作为一个体积单位．只要直接把单位正方体尽可能地堆在所量的几何体内，来确定所量几何体的体积的量数．因此我们容易得到正方体和长方体的体积公式，但是不容易得到一般棱柱的体积公式．(可以先把一般棱柱分割成三棱柱，三棱柱补成平行六面体，平行六面体割补成长方体)

4)如何找到长方体的体积和一般棱柱的体积之间的关系？

1．从已知到未知，从特殊到一般：

首先想到已经学过的正方体、长方体的体积公式，然后探究一般棱柱的体积公式．

(1)(－棱长)；

(2)_长方体(－长，－宽，－高，－底面积)

引例：青藏铁路是西部大开发标志性工程，计划投资约262亿元，铁路全长1142公里，是世界上海拔最高，线路最长，穿越冻土里程最长的高原铁路．针对不同情况的多年冻土，有不同的解决办法与技术．比如埋设热棒或通风管，就是在路堤中埋设直径30厘米左右的金属或混凝土横向通风管，可以有效降低路基温度；也可以采用抛石路基，即用碎块石填筑路基，利用填石路基的通风透气性，隔阻热空气下移，同时吸入冷量，起到保护冻土的作用；在少数极不稳定冻土地段修建低架旱桥，工程效果有保证，但造价高．

假设在青藏铁路的某段路基需要用碎石铺垫．已知路基的形状尺寸如图所示(单位：米)，问每修建1千米铁路需要碎石多少立方米？

说明：在生产实际中，经常遇到体积的计算问题，如兴修水利、修建道路需要计算土方，修建粮仓、水池需要计算建材数量和容积．因此有必要研究几何体的体积计算．上例就是一个直四棱柱的体积计算问题．

提出问题：棱柱的体积如何计算？

16． 求证：不论为什么实数，直线都通过一定点

15．两条直线和的交点在第四象限，求的取值范围．

14．求两平行线：，：的距离.

13．根据下列各条件写出直线的方程，并且化成一般式：

(1)斜率是，经过点A(8,－2)；(2)经过点B(4,2)，平行于轴；

(3)在轴和轴上的截距分别是、－3；(4)经过两点.

10.已知，当时，直线的斜率 =　　　　 ；当且时，直线的斜率为　　　 ,倾斜角为　　　

11　以点为端点的线段的中垂线的方程是　　　　　　　　

12　过点平行的直线的方程是