
1. 如图4所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,B、C为水平的,其距离d=0.50 m。盆边缘的高度为h=0.30 m。在A处放一个质量为m的小物块并让其从静止出发下滑。已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数为μ=0.10。小物块在盆内来回滑动,最后停下来,则停的地点到B的距离为( )
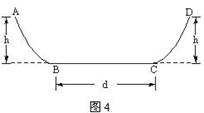
如图4所示,ABCD是一个盆式容器,盆内侧壁与盆底BC的连接处都是一段与BC相切的圆弧,B、C为水平的,其距离d=0.50 m。盆边缘的高度为h=0.30 m。在A处放一个质量为m的小物块并让其从静止出发下滑。已知盆内侧壁是光滑的,而盆底BC面与小物块间的动摩擦因数为μ=0.10。小物块在盆内来回滑动,最后停下来,则停的地点到B的距离为( )
A.0.50 m B.0.25 m 
C.0.10 m D.0
2.老师小结:
(1)本节课的主要内容有两个:一是棱柱体积公式的推导.所采用的方法是利用祖暅原理,根据长方体的体积公式推导出棱柱的体积公式.应用祖暅原理可以根据已知几何体的体积求未知几何体的体积,这是一种求体积的办法,但要注意是否满足祖暅原理的条件.二是应用棱柱体积公式解决实际问题.在具体问题中要结合直观图,认真分析棱柱的底面积和高从而得到体积.
(2)本节课的数学思想方法主要体现在:由特殊棱柱--长方体的体积推导一般棱柱的体积,再根据一般棱柱的体积公式去解决具体问题中的特殊棱柱的体积,这种从特殊到一般,再从一般到特殊的归纳演绎的数学思想方法常常是学习数学概念的方法.从两个平面图形面积相等的条件类比猜想到两个空间图形体积相等的条件,然后在实践中理解论证,这种归纳、猜想、论证的数学思想方法经常用在发现数学原理和规律的过程中.在祖暅原理的理解中,体会由“截线都相等”推出“面积相等”,由“面积都相等”推出“体积相等”的辩证法的思想,实际上就是微积分的思想.
(3)若用割补的办法把一般棱柱转化为长方体也是可以的,但是由于课堂时间有限,留给同学们课后研究.
教学设计说明
体积的计算在现实中大量存在,学生对它们已有一定的感性认识.本节课用一个需要利用棱柱体积公式才能解决的实际问题引入,说明研究棱柱体积公式的必要性.这个实例是学生熟知的青藏铁路的冻土解决方案,具有很强的现实意义,
本节课的重点是棱柱体积公式的推导.首先启发学生思考体积是如何度量的.从长度的度量、面积的度量都是必须先找一个度量单位,类比得出体积的度量也是必须先找一个度量单位即单位正方体所占空间的大小.然后得到正方体和长方体的体积公式,但是一般棱柱体积的公式不容易得到.通过几何画板的动态演示,把平面上等底等高的平行四边形面积相等、等底等高的三角形面积相等的本质揭示出来,即若用平行于底边的任意直线截两个平面图形得到的截线长度总相等,则两个平面图形面积相等.然后由学生从平面到空间类比猜想得出祖暅原理的基本内容,并且利用实物道具的“小试验”验证猜想.首先讨论推斜前后的两叠裁切相同的纸的体积是否相等,主要把握整叠纸张的大小、顺序和厚度不变三个共同特点.在祖暅原理内容的理解中,使学生体会从“面积都相等”得到“体积相等”的辩证法的思想.然后,把“小试验”中的裁切相同的纸换成一摞不同的书,让学生继续讨论这摞书经过推斜后是否体积相等,从棱柱到非棱柱,进一步理解祖暅原理的含义.因为祖暅原理的发现是从实践中得来的,因此设置一些从简单到复杂,从特殊到一般的“小试验”,让学生观察试验、发现规律、总结规律.通过设置试验和启发引导,呈现原理的发现过程.用几何画板动态演示“任意一个平面截两个几何体所得截面的各种位置”,帮助学生理解祖暅原理中的“任意”和“总相等”,有效地突破教学难点.最后说明祖暅原理实际上是一个定理,但证明它需要用到高等数学的相关知识,中学阶段不能证明.它只能判定两个几何体是否体积相等,不能用它具体求出某几何体的体积.要想完成求体积的任务,还必须已知一个几何体的体积作为基础.接下来,学生利用长方体的体积公式和祖暅原理很容易就可以推导出棱柱体积公式.这个过程体现了从已知到未知、从特殊到一般的学习数学概念的基本方法.最后,通过介绍祖冲之父子及我国古代数学家和西方数学家对几何体体积的研究,揭示数学发展过程,体现数学的人文精神,激发学生学习数学的热情.
巩固和应用中的例题的选取尽量体现在实际生活中的运用,以激发学生学习的兴趣,增强数学的应用意识.
1.学生小结:
3.
 例3.一个造桥用的钢筋混凝土预制件的尺寸如图所示(单位:米),浇制一个这样的预制件需要多少立方米混凝土?(钢筋体积略去不计,精确到
例3.一个造桥用的钢筋混凝土预制件的尺寸如图所示(单位:米),浇制一个这样的预制件需要多少立方米混凝土?(钢筋体积略去不计,精确到 立方米)
立方米)
解:将预制件看成由一个长方体挖去一个底面为等腰梯形的直四棱柱.
 (平方米),
(平方米),
 (立方米).
(立方米).
答:略.
说明:在实际问题中,可能需要将几何体割、补成棱柱,然后计算其体积,本题意在提高学生这方面的能力.
2.例2.已知三棱柱 的底面为直角三角形,两直角边
的底面为直角三角形,两直角边 和
和 的长分别为
的长分别为 和
和 ,侧棱
,侧棱 的长为
的长为 ,求满足下列条件的三棱柱的体积:
,求满足下列条件的三棱柱的体积:
(1)
侧棱 垂直于底面;
垂直于底面;
(2)
侧棱 与底面所成的角为
与底面所成的角为 .
.
解:(1)因为侧棱 底面
底面 ,所以三棱柱的高
,所以三棱柱的高 等于侧棱
等于侧棱 的长,而底面三角形
的长,而底面三角形 的面积
的面积 ,于是三棱柱的体积
,于是三棱柱的体积
 .
.
(2)如图所示,过 作平面
作平面 的垂线,垂足为
的垂线,垂足为 ,
,
 于是
于是 为三棱柱的高.因为侧棱
为三棱柱的高.因为侧棱 与底面所成的角为
与底面所成的角为 ,所以
,所以 ,可计算得
,可计算得
又由(1)可知底面三角形 的面积
的面积 ,故三棱柱的体积
,故三棱柱的体积
1.引例的解答:这是一个底面是梯形的直四棱柱的体积问题.
 .
.
8.祖暅原理的简单应用:
(1) 底面积和高都相等的圆柱和长方体的体积相等吗?
(2) 底面积和高都相等的斜六棱柱和三棱锥的体积相等吗?
7. 介绍祖冲之父子及我国古代数学家和西方数学家对几何体体积的研究:
中国古代数学,在魏晋南北朝达到新的高峰.这一时期的代表人物是刘徽(公元263年左右)、祖冲之(429-500)和他的儿子祖暅.刘徽为《九章算术》作注,祖冲之父子在此基础上撰写了《缀术》等著作.祖冲之精确地计算圆周率,提出约率和密率,是世界数学史上的重大成就.他们三人还先后研究并最终给出了球的体积公式.在这过程中,他们利用了“夫叠棊成立积,缘幂势既同,则积不容异”的原理,唐朝的李淳风在为《九章算术》作注时称求球体体积公式的方法是“祖暅之开立园术”,祖暅之即祖暅,因此我国称之为祖暅原理.意大利数学家卡瓦列里1635年提出了相同的原理,西方称之为卡瓦列里原理,为微积分学创立作了准备.
6. 利用祖暅原理推导棱柱体积公式:
(1)利用祖暅原理推导棱柱体积,需要构造一个几何体,此几何体必须符合两个条件: 它的计算公式是已知的;
它的计算公式是已知的; 它符合祖暅原理的条件,即该几何体与棱柱能夹在两个平行平面之间,且用平行于这两个平面的任意一个平面去截它们时,截得的截面面积总相等.
它符合祖暅原理的条件,即该几何体与棱柱能夹在两个平行平面之间,且用平行于这两个平面的任意一个平面去截它们时,截得的截面面积总相等.
(2)方法:如果一个棱柱与一个长方体的高相同(都为 )且底面面积相等(都为
)且底面面积相等(都为 ),那么当我们用一个与底面平行的平面去截它们时,可以证明截面的面积都等于各自底面的面积
),那么当我们用一个与底面平行的平面去截它们时,可以证明截面的面积都等于各自底面的面积 ,根据祖暅原理可知,棱柱的体积与长方体的体积相等,即
,根据祖暅原理可知,棱柱的体积与长方体的体积相等,即 ,其中
,其中 表示棱柱的体积,
表示棱柱的体积, 表示棱柱底面的面积,
表示棱柱底面的面积, 表示棱柱的高.
表示棱柱的高.
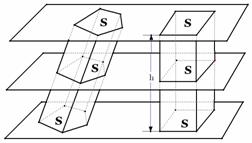
5.祖暅原理:“夫叠棊成立积,缘幂势既同,则积不容异”.
(1)内容解释:这里的“幂”是指水平截面的面积,“势”是指高.
即体积可看成是由面积叠加而成,用一组平行平面截两个空间图形,若在任意等高处的截面面积都对应相等,则两空间图形的体积必然相等.
还可表达为:夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.(我国古代数学家祖暅在实践的基础上,明确肯定了这一点)
(2)由“面积都相等”推出“体积相等”,体会辩证法的思想.
(3)祖暅原理实际上是一个定理,但证明它需要用到高等数学的相关知识,中学阶段不能证明.它只能判定两个几何体是否等积,不能用它具体求出某几何体的体积.要想完成求体积的任务,还必须已知一个几何体的体积作为基础.
(4)几何画板动态演示任意一个平面截两个几何体所得截面的各种位置.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com