(二)主要方法：

1．讨论函数单调性必须在其定义域内进行，因此要研究函数单调性必须先求函数的定义域，函数的单调区间是定义域的子集；

2．判断函数的单调性的方法有：(1)用定义；(2)用已知函数的单调性；(3)利用函数的导数．

3．注意函数的单调性的应用；

4．注意分类讨论与数形结合的应用．

(一)主要知识：

1、函数单调性的定义；

2、判断函数单调性(求单调区间)的方法：

(1)从定义入手

(2)从导数入手

(3)从图象入手

(4)从熟悉的函数入手

(5)从复合函数的单调性规律入手

注：先求函数的定义域

3、函数单调性的证明：定义法；导数法。

4、一般规律

(1)若f(x),g(x)均为增函数，则f(x)+g(x)仍为增函数；

(2)若f(x)为增函数，则-f(x)为减函数；

(3)互为反函数的两个函数有相同的单调性；

(4)设是定义在M上的函数，若f(x)与g(x)的单调性相反，则在M上是减函数；若f(x)与g(x)的单调性相同，则在M上是增函数。

19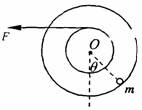．半径分别为r和2r的两个质量不计的圆盘，共轴固定连结在一起，可以绕水平轴O无摩擦转动，大圆盘的边缘上固定有一个质量为m的质点，小圆盘上绕有细绳．开始时圆盘静止， 质点处在水平轴O的正下方位置．现以水平恒力F拉细绳， 使两圆盘转动，若恒力 F=mg，两圆盘转过的角度θ=　　　　　 时，质点m的速度最大．若圆盘转过的最大角度θ=π/3，则此时恒力F=　　　　 。

答案　 ，

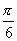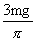
[1D 2BC 3C 4BC 5B 6BCD7CD 8AC 9C 10B 11BCD]

18．一内壁光滑的环形细圆管,位于竖直平面内,环的半径为R(比细管的半径大得多).在圆管中有两个直径与细管内径相同的小球(可视为质点), A球的质量为m ₁,B球的质量为m ₂,它们沿环形圆管顺时针运动,经过最低点时的速度都为v ₀.设A球运动到最低点时,B球恰好运动到最高点.若要此时两球作用于圆管的合外力为零,那么m ₁、m ₂、R与v ₀应满足的关系式是　　　　　 .　

答案：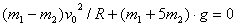

17.有三根长度皆为l＝1.00 m的不可伸长的绝缘轻线，其中两根的一端固定在天花板上的O点，另一端分别拴有质量皆为m＝1.00×10^{－2 kg}的带电小球A和B，它们的电量分别为－q和+q，q＝1.00×10^－7C。A、B之间用第三根线连接起来。空间中存在大小为E＝1.00×10⁶N/C的匀强电场，场强方向沿水平向右，平衡时A、B球的位置如图所示。现将O、B之间的线烧断，由于有空气阻力，A、B球最后会达到新的平衡位置。求最后两球的机械能与电势能的总和与烧断前相比改变了多少。(不计两带电小球间相互作用的静电力)

答案 W＝6.8×10^－2J　　　　　　　　　　

16.质量m=1.5 kg的物块(可视为质点)在水平恒力F作用下，从水平面上A点由静止开始运动，运动一段距离撤去该力，物块继续滑行t=2.0 s停在B点，已知A、B两点间的距离s=5.0 m，物块与水平面间的动摩擦因数μ=0.20，求恒力F多大。(g=10 m/s²)

答案 F=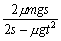=15 N 　　　　

15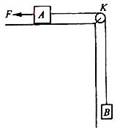． 如图所示，在水平桌面的边角处有一轻质光滑的定滑轮K，一条不可伸长的轻绳绕过K分别与物块A、B相连，A、B的质量分别为m_A、m_B。开始时系统处于静止状态。现用一水平恒力F拉物块A，使物块B上升。已经当B上升距离为h时，B的速度为υ。求此过程中物块A克服摩擦力所做的功。重力加速度为g。

答案 W=Fh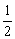－(m_A+m_B)v²－m_Bgh

14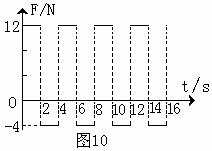．一个质量为4kg的物体静止在足够大的水平地面上，物体与地面间的动摩擦因数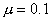。从t=0开始，物体受到一个大小和方向呈周期性变化的水平力F作用，力F随时间的变化规律如图10所示。求83秒内物体的位移大小和力F对物体所做的功。g取。

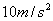答案　 167m　 676J

13.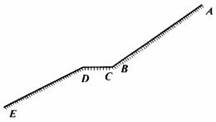下图是简化后的跳台滑雪的雪道示意图。整个雪道由倾斜的助滑雪道AB和着陆雪道DE，以及水平的起跳平台CD组成，AB与CD圆滑连接。　运动员从助滑雪道AB上由静止开始，在重力作用下，滑到D点水平飞出，不计飞行中的空气阻力，经2 s在水平方向飞行了60 m，落在着陆雪道DE上。已知从B点到D点运动员的速度大小不变。(g取l0 m/s²)求:

(1)运动员在AB段下滑到B点的速度大小；

(2)若不计阻力，运动员在AB段下滑过程中下降的高度；

(3)若运动员的质量为60 kg，在AB段下降的实际高度是50 m，此过程中他克服阻力所做的功。

答案(1)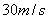(2)(3)

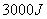
12.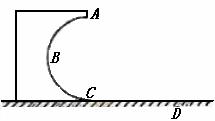如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R＝0.5 m，轨道在C处与水平地面相切。在C处放一小物块，给它一水平向左的初速度v₀＝5 m/s，结果它沿CBA运动，通过A点，最后落在水平面上的D点，求C、D间的距离s。取重力加速度g＝10m/s²。

答案　S=1m