7．如图正四面体中，D、E是棱PC上不重合的两点；F、H分别是棱PA、PB上的点，且与P点不重合．

求证：EF和DH是异面直线．

§6.2直线与平面之间的位置关系

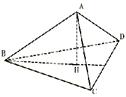
6．在空间四边形ABCD中，AB⊥CD，AH⊥平面BCD，

求证：BH⊥CD

5.关于直角AOB在定平面α内的射影有如下判断：①可能是0°的角；②可能是锐角；③可能是直角；④可能是钝角；⑤可能是180°的角. 其中正确判断的序号是_____.(注：把你认为正确的序号都填上).

4.长方体中，

则所成角的大小为_　 ___.

3.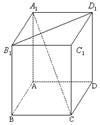 在棱长为a的正方体ABCD－A₁B₁C₁D₁中，体对角线DB₁与面对角线BC₁所成的角是　　　 ，它们的距离是　　 .

2. 两个正方形ABCD、ABEF所在的平面互相垂直，则异面直线AC和BF所成角的大小为　　 　．

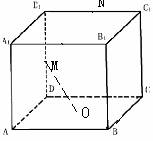[例1]在正方体ABCD-ABCD中,O是底面ABCD的中心，M、N分别是棱DD、DC的中点，则直线OM(　　 ).

A .是AC和MN的公垂线.　 B .垂直于AC但不垂直于MN.

C .垂直于MN，但不垂直于AC.　 D .与AC、MN都不垂直.

错解:B.

错因：学生观察能力较差，找不出三垂线定理中的射影.

正解：A.　

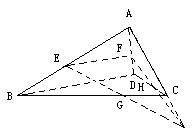[例2]如图，已知在空间四边形ABCD中,E,F分别是AB,AD的中点，G,H分别是BC,CD上的点,且,求证:直线EG,FH,AC相交于一点.

错解：证明：、F分别是AB,AD的中点,

∥BD,EF=BD,

又, GH∥BD,GH=BD,

　　 四边形EFGH是梯形，设两腰EG,FH相交于一点T,

,F分别是AD.AC与FH交于一点.

直线EG,FH,AC相交于一点

正解：证明：、F分别是AB,AD的中点,

　 ∥BD,EF=BD,

又,

　　 GH∥BD,GH=BD,

四边形EFGH是梯形，设两腰EG,FH相交于一点T,

平面ABC,FH平面ACD,

T面ABC,且T面ACD,又平面ABC平面ACD=AC,

,直线EG,FH,AC相交于一点T.

[例3]判断：若a,b是两条异面直线，P为空间任意一点，则过P点有且仅有一个平面与a,b都平行.

错解：认为正确.

错因：空间想像力不够.忽略P在其中一条线上，或a与P确定平面恰好与b平行，此时就不能过P作平面与a平行.

正解：假命题．

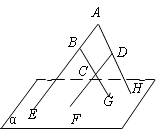　[例4] 如图，在四边形ABCD中，已知AB∥CD，直线AB，BC，AD，DC分别与平面α相交于点E，G，H，F．求证：E，F，G，H四点必定共线(在同一条直线上)． 　分析：先确定一个平面，然后证明相关直线在这个平面内，最后证明四点共线． 　证明 ∵ AB//CD， AB，CD确定一个平面β． 　又∵AB ∩α＝E，AB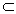β， Eα，Eβ， 　即 E为平面α与β的一个公共点． 同理可证F，G，H均为平面α与β的公共点．

∵ 两个平面有公共点，它们有且只有一条通过公共点的公共直线， ∴ E，F，G，H四点必定共线． 　点　评：在立体几何的问题中，证明若干点共线时，先证明这些点都是某两平面的公共点，而后得出这些点都在二平面的交线上的结论．

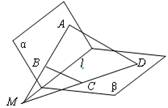
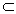[例5]如图，已知平面α，β，且α∩β＝．设梯形ABCD中，AD∥BC，且ABα，CD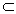β，求证：AB，CD，共点(相交于一点)． 　 分析：AB，CD是梯形ABCD的两条腰，必定相交于一点M，只要证明M在上，而是两个平面α，β的交线，因此，只要证明M∈α，且M∈β即可．

证明： ∵ 梯形ABCD中，AD∥BC， 　∴AB，CD是梯形ABCD的两条腰． 　∴ AB，CD必定相交于一点， 　设 AB ∩CD＝M． 　又∵ AB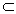α，CD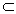β，∴ M∈α，且M∈β． 　∴ M∈α∩β． 　又∵ α∩β＝，∴ M∈， 　即 AB，CD，共点．

　点　评：证明多条直线共点时，与证明多点共线是一样的．

　[例6]已知：a，b，c，d是不共点且两两相交的四条直线，求证：a，b，c，d共面． 　 分析：弄清楚四条直线不共点且两两相交的含义：四条直线不共点，包括有三条直线共点的情况；两两相交是指任何两条直线都相交．在此基础上，根据平面的性质，确定一个平面，再证明所有的直线都在这个平面内．

证明 1º若当四条直线中有三条相交于一点，不妨设a，b，c相交于一点　A　 ∴ 直线d和A确定一个平面α．

　又设直线d与a，b，c分别相交于E，F，G， 则 A，E，F，G∈α． ∵ A，E∈α，A，E∈a， ∴ a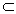α． 同理可证 b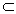α，c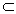α． ∴ a，b，c，d在同一平面α内． 2º当四条直线中任何三条都不共点时，如图． ∵ 这四条直线两两相交， 则设相交直线a，b确定一个平面α． 设直线c与a，b分别交于点H，K， 则 H，K∈α． 又∵ H，K∈c，∴ c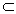α． 同理可证 d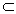α． ∴ a，b，c，d四条直线在同一平面α内．

点　评：证明若干条线(或若干个点)共面的一般步骤是：首先由题给条件中的部分线(或点)确定一个平面，然后再证明其余的线(或点)均在这个平面内．本题最容易忽视“三线共点”这一种情况．因此，在分析题意时，应仔细推敲问题中每一句话的含义．

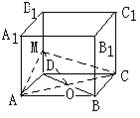[例7] 在立方体ABCD－A₁B₁C₁D₁中， 　(1)找出平面AC的斜线BD₁在平面AC内的射影； 　(2)直线BD₁和直线AC的位置关系如何？ 　(3)直线BD₁和直线AC所成的角是多少度？

解：(1)连结BD, 交AC于点O .

(2)BD₁和AC是异面直线.

(3)过O作BD₁的平行线交DD₁于点M，连结MA、MC，则∠MOA或其补角即为异面直线AC和BD₁所成的角.

不难得到MA＝MC，而O为AC的中点，因此MO⊥AC，即∠MOA＝90°， ∴异面直线BD₁与AC所成的角为90°.

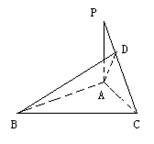
[例8] 已知：在直角三角形ABC中，A为直角，PA⊥平面ABC，BD⊥PC，垂足为D，求证：AD⊥PC 证明：∵　PA ⊥平面ABC∴　PA⊥BA 　又∵　BA⊥AC ∴　BA⊥平面PAC 　∴　AD是BD在平面PAC内的射影 　又∵　BD⊥PC　 ∴　AD⊥PC.(三垂线定理的逆定理) 四、典型习题导练

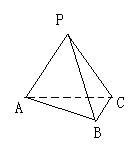
1．如图, P是△ABC所在平面外一点，连结PA、PB、PC后，在包括AB、BC、CA的六条棱所在的直线中，异面直线的对数为(　 )

　 A.2对　 B.3对　 C.4对　 D.6对

5．异面直线的证明一般用反证法、异面直线的判定方法：如图，如果b,A且A,a,则a与b异面.

4．异面直线的距离是指夹在两异面直线之间公垂线段的长度.求两条异面直线的距离关键是找到它们的公垂线.

3．异面直线的公垂线要求和两条异面直线垂直并且相交，