4．球面上两点间的距离是指经过这两点的球的大圆的劣弧的长，关键在于画出经过两点的大圆以及小圆.

3．空间距离的计算一般将其转化为两点间的距离.求点到平面距离时，可先找出点在平面内的射影(可用两个平面垂直的性质)，也可用等体积转换法求之.另外要注意垂直的作用.球心到截面圆心的距离由勾股定理得

2．求二面角大小时，关键是找二面角的平面角，可充分利用定义法或垂面法等.

1．求空间角的大小时，一般将其转化为平面上的角来求，具体地将其转化为某三角形的一个内角.

2．掌握给出公垂线的两条异面直线的距离、点到直线(或平面)的距离、直线与平面的距离及两平行平面间距离的求法.

1.掌握两条异面直线所成的角、直线与平面所成的角及二面角，掌握上述三类空间角的作法及运算.

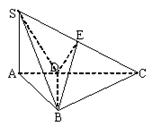
5. 已知：如图，SA⊥平面ABC，AB⊥BC，DE垂直平分SC，且分别交AC、SC于D、E，又SA=AB，SB=BC，求二面角E－BD－C的度数.

§6.4空间角和距离

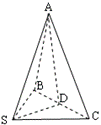
4.如图，过S引三条长度相等但不共面的线段SA、SB、SC，

且∠ASB=∠ASC=60°，∠BSC=90°.

　 求证：平面ABC⊥平面BSC. 　　　　　　

3.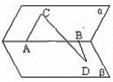 在60°二面角的棱上，有两个点A、B，AC、BD分别是在这个二面角的两个面内垂直于AB的线段．已知：AB＝4cm，AC=6cm，BD＝8cm，求CD长．

2. 过正方形ABCD的顶点A作线段PA⊥平面ABCD，且PA=AB，则平面ABP与平面CDP所成二面角(小于或等于90°)的度数是_____．