1、25℃时，将某强酸和某强碱溶液按1∶10的体积比混合后溶液恰好中性，则混合前此强酸与强碱溶液的pH之和是

A.12　　　　　　 B.13　　　　　　 C.14　　　　　　 D.15

4、说明

(1)功的概念起源于早期工业革命的需要，为了比较蒸汽机的效益，工程师用机器举起物体的重量与高度的乘积来度量机器的输出，称为功。

(2)19世纪法国的科学家科里奥利把作用力和力的方向上的位移的乘积叫做运动的功。

(3)功的重要意义在于决定能量的变化。

实例探究

对“功”的理解

例1：水流从高处落下，对水轮机做3×10⁸J 的功，对这句话的正确理解是(　　　 )

A．水流在对水轮机做功前，具有3×10⁸J的能量

B．水流在对水轮机做功时，具有 3×10⁸J的能量

C．水流在对水轮机做功后，具有 3×10⁸J的能量

D．水流在对水轮机做功的过程中，能量减少3×10⁸J

解析：本题考查了功和能的关系，并且同实际中的科技应用联系起来。

解：根据“功是能量转化的量度”可知，水流在对水轮机做功的过程中，有能量参与转化，水流对水轮机做了3×10⁸J的功，则有3×10⁸J的机械能减少了。故答案应选D。

点拨：功是能量转化的量度是指做功的过程就是能量转化的过程。做了多少功，就有多少能量发生转化，绝不能说功是能量的量度。

关于“功”的计算

例1：用水平恒力F作用在质量为M的物体上，使之在光滑的水平面上沿力的方向移动距离s，恒力做功为w₁，再用该恒力作用于质量为m(m<M)的物体上，使之在粗糙的水平面上移动同样距离s，恒力做功为w₂，则两次恒力做功的关系是(　 ) 　A．w₁>w₂　B．w₁<w₂　C．w₁=w₂　D．无法判断 　分析：在粗糙水平面上移动一段距离，跟在光滑水平面上移动的相同距离，对力F做功来说，w=FS是相同的，即W₁=W₂。 　解：正确选项为C． 点评：求功时，必须要明确哪个力在哪个过程中的功。根据功的定义，力F所做的功与F的大小及在F的方向上发生的位移大小的乘积有关，与物体是否受其它力及物体的运动状态等其它因素均无关．即力做功具有独立性。

例2：如图所示，拉力F使质量为m的物体匀速地沿着长为L倾角为 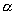的斜面的一端向上滑到另一端，物体与斜面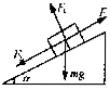间的动摩擦因数为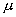，分别求作用在物体上各力对物体所作的功．

分析：选物体为研究对象，其受力为拉力F，重力mg，弹力F₁，摩擦力F₂。 解：(1)拉力F对物体所做的功为　W_F=FL 　由于物体作匀速运动，故

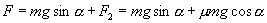　所以　

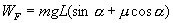　即拉力F对物体做正功，此拉力F，一般称为动力或牵引力。 (2)重力mg对物体所做的功为：

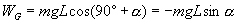
即重力对物体做负功，即亦物体克服重力所做的功为 。

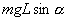(3)摩擦力对物体所做的功为

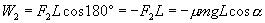
即摩擦力对物体做负功．也可以说是物体克服摩擦力做了功

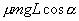
(4)弹力F₁对物体所做的功为

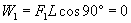
即弹力对物体不做功．

点评：讲功必须分清是哪个力做的功，在解题时一定要注意题目中是求哪个力做的功，正确找出力F、位移s和夹角 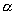的关系。

例3：如图3所示，ABCD为画在水平地面上的正方形，其边长为a，P为静止于A点的物体。用水平力F沿直线 AB拉物体缓慢滑动到B点停下，然后仍用水平力F沿直线BC拉物体滑动到C点停下，接下来仍用水平力F沿直线CD拉物体滑动到D点停下，最后仍用水平力F沿直线DA拉物体滑动到A点停下。若后三段运动中物体也是缓慢的，求全过程中水平力F对物体所做的功是多少？

(此例题先让学生做，然后找出一个所得结果是W=0的学生发言，此时会有学生反对，并能说出W=4Fa才是正确结果。让后者讲其思路和做法，然后总结，使学生明确在每一段位移a中，力F都与a同方向，做功为Fa，四个过程加起来就是4Fa。)

点评：功的概念中的位移是在这个力的方向上的位移，而不能简单地与物体运动的位移画等号。要结合物理过程做具体分析。

3、几个力做功的计算

　　 几个力对物体所做的功可以用下述方法求解：

(1)求出各个力所做的功，则总功等于各个力所做功的代数和；

(2)求出几个力的合力，则总功等于合力所做的功。

2、对正功和负功的学习

(1)当α=π/2时，cosα=0，W=0。力F和位移s的方向垂直时，力F不做功；

(2)当α＜π/2时，cosα＞0，W＞0。这表示力F对物体做正功；

(3)当π/2＜α≤π时，cosα＜0，W＜0。这表示力F对物体做负功。

注意：

(1)功的正负表示是动力对物体做功还是阻力对物体做功。

(2)功的正负是借以区别谁对谁做功的标志。

(3)一个力对物体做负功，往往说成物体克服这个力做功。

1、推导功的表达式

W = F s cosα 　或　 W = F s cosα

功的单位是焦耳(J)　　　　 1J＝1N·m

3、几个力做功的计算

刚才我们学习了一个力对物体所做功的求解方法，而物体所受到的力往往不只一个，那么，如何求解这几个力对物体所做的功呢?

如图所示，一个物体在拉力F1的作用下，水平向右移动位移为s，求各个力对物体做的功是多少?各个力对物体所做功的代数和如何? 物体所受的合力是多少?合力所做的功是多少?

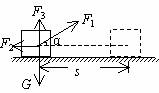
解析：物体受到拉力F₁、滑动摩擦力F₂、重力G、支持力F₃的作用。重力和支持力不做功，因为它们和位移的夹角为90°；F₁所做的功为：W₁=Fscosα，滑动摩擦力F₂所做的功为：W₂=F₂scos180°=-F₂s。各个力对物体所做功的代数和为：W=(F1cosα-F₂)s

故：根据正交分解法求得物体所受的合力F=F₁cosα-F₂ 合力方向向右，与位移同向；合力所做的功为：W=Fscos0°=(F₁cosα-F₂)s

总结：当物体在几个力的共同作用下发生一段位移时，这几个力对物体所做的功可以用下述方法求解：

(1)求出各个力所做的功，则总功等于各个力所做功的代数和；

(2)求出各个力的合力，则总功等于合力所做的功。

例3：一个质量m=2kg的物体，受到与水平方向成37°角斜向上方的拉力F1=10N，在水平地面上移动的距离s=2m。物体与地面间的滑动摩擦力F2=4.2N。求外力对物体所做的总功。

解析：拉力F1对物体所做的功为W1= F1scos37°=16J。

摩擦力F2对物体所做的功为W2= F2scos180°= -8.4J。

外力对物体所做的总功W=W1+W2=7.6J。

板书设计：

第二节　　 功

1、推导功的表达式

(1)如果力的方向与物体的运动方向一致，该怎样计算功呢？

　物体m在水平力F的作用下水平向前行驶的位移为s，如图1所示，求力F对物体所做的功。

　　 在问题一中，力和位移方向一致，这时功等于力跟物体在力的方向上移动的距离的乘积。

W = F s

(2)如果力的方向与物体的运动方向成某一角度，该怎样计算功呢？物体m在与水平方向成α角的力F的作用下，沿水平方向向前行驶的距离为s，如图2所示，求力F对物体所做的功。

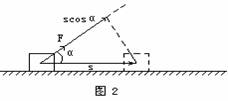
　　 分析并得出这一位移为s cos α。至此按功的前一公式即可得到如下：

计算公式： 　W = F s cosα

按此公式考虑(再根据公式W=Fs做启发式提问)，只要F与s在同一直线上，乘起来就可以求得力对物体所做的功。在图2中，我们是将位移分解到F的方向上，如果我们将力F分解到物体位移s的方向上，看看能得到什么结果？

由于物体所受力的方向与运动方向成一夹角α，可根据力F的作用效果把F沿两个方向分解：即跟位移方向一致的分力F1，跟位移方向垂直的分力F2，如图所示：

据做功的两个不可缺少的因素可知：分力F₁对物体所做的功等于F₁s。而分力F­₂的方向跟位移的方向垂直，物体在F­₂的方向上没有发生位移，所以分力F₂所做的功等于零。所以，力F所做的功W=W₁+W₂=W₁=F₁s=Fscosα

力F对物体所做的功等于力的大小、位移的大小、力和位移夹角的余弦这三者的乘积。即：

W = F s cosα

W表示力对物体所做的功，F表示物体所受到的力，s物体所发生的位移，α力F和位移之间的夹角。功的公式还可理解成在位移方向的分力与位移的乘积，或力与位移在力的方向的分量的乘积。

例题1：F=100N、s=5m、α=37°，计算功W？ W=400N·m。就此说明1N·m这个功的大小被规定为功的单位，为方便起见，取名为焦耳，符号为J，即1J=1N·m。

在国际单位制中，功的单位是焦耳(J)　　　　 1J＝1N·m

初中我们学过做功的两个因素是什么?(一是作用在物体上的力，二是物体在力的方向上移动的距离。)

扩展：高中我们已学习了位移，所以做功的两个要素我们可以认为是：①作用在物体上的力；②物体在力的方向上移动的位移。

导入：一个物体受到力的作用，且在力的方向上移动了一段位移，这时，我们就说这个力对物体做了功。在初中学习功的概念时，强调物体运动方向和力的方向的一致性，如果力的方向与物体的运动方向不一致呢？相反呢？力对物体做不做功？若做了功，又做了多少功？怎样计算这些功呢？本节课我们来继续学习有关功的知识，在初中的基础上进行扩展。

21．

万事万物皆有“源”：活水源的生机来源于涓涓的泉水，朱熹的睿智来源于博览群书，白洋淀妇女们的勇敢来源于夫妻、家国之爱，《红楼梦》的不朽来源于作者对中国文化的精深理解与对世态人情的深刻体验……

请结合社会生活，以“　　　　　 之源”为题，谈谈你对“源”的认识。

要求：

1、　 把题目补充完整。

2、　 不少于700字。