31.小概率事件的含义

　　 发生概率一般不超过5%的事件，即事件在一次试验中几乎不可能发生

　　 假设检验方法的基本思想:首先，假设总体应是或近似为正态总体，然后，依照小概率事件几乎不可能在一次试验中发生的原理对试验结果进行分析

　　 假设检验方法的操作程序，即“三步曲”

　　 一是提出统计假设，教科书中的统计假设总体是正态总体；

二是确定一次试验中的a值是否落入(μ-3σ，μ+3σ)；

三是作出判断

30．非标准正态总体在某区间内取值的概率:可以通过转化成标准正态总体，然后查标准正态分布表即可 在这里重点掌握如何转化 首先要掌握正态总体的均值和标准差，然后进行相应的转化

29.标准正态分布表

标准正态总体在正态总体的研究中有非常重要的地位，为此专门制作了“标准正态分布表”．在这个表中，对应于的值是指总体取值小于的概率，即 ，．

若，则．

利用标准正态分布表，可以求出标准正态总体在任意区间内取值的概率，即直线，与正态曲线、x轴所围成的曲边梯形的面积．

28.标准正态总体的概率问题:

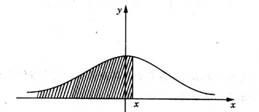
对于标准正态总体N(0，1)，是总体取值小于的概率，

即　　　　　 ，

其中，图中阴影部分的面积表示为概率 只要有标准正态分布表即可查表解决.从图中不难发现:当时，；而当时，Φ(0)=0.5

27．标准正态曲线:当μ=0、σ=l时，正态总体称为标准正态总体，其相应的函数表示式是，(-∞＜x＜+∞)

其相应的曲线称为标准正态曲线

标准正态总体N(0，1)在正态总体的研究中占有重要的地位 任何正态分布的概率问题均可转化成标准正态分布的概率问题

26．正态曲线的性质：

(1)曲线在x轴的上方，与x轴不相交

(2)曲线关于直线x=μ对称

(3)当x=μ时，曲线位于最高点

(4)当x＜μ时，曲线上升(增函数)；当x＞μ时，曲线下降(减函数) 并且当曲线向左、右两边无限延伸时，以x轴为渐近线，向它无限靠近

(5)μ一定时，曲线的形状由σ确定

σ越大，曲线越“矮胖”，总体分布越分散；

σ越小．曲线越“高”．总体分布越集中：

五条性质中前三条学生较易掌握，后两条较难理解，因此在讲授时应运用数形结合的原则，采用对比教学

25．正态分布)是由均值μ和标准差σ唯一决定的分布

24．正态分布密度函数：

，(σ＞0)

其中π是圆周率；e是自然对数的底；x是随机变量的取值；μ为正态分布的均值；σ是正态分布的标准差.正态分布一般记为

23.总体密度曲线:样本容量越大，所分组数越多，各组的频率就越接近于总体在相应各组取值的概率．设想样本容量无限增大，分组的组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线．

它反映了总体在各个范围内取值的概率．根据这条曲线，可求出总体在区间(a，b)内取值的概率等于总体密度曲线，直线x=a，x=b及x轴所围图形的面积．

22.不放回抽样和放回抽样:在抽样中，如果每次抽出个体后不再将它放回总体，称这样的抽样为不放回抽样；如果每次抽出个体后再将它放回总体，称这样的抽样为放回抽样．

随机抽样、系统抽样、分层抽样都是不放回抽样