19.(本小题满分14分)

已知椭圆G的中心在坐标原点,长轴在轴上,离心率为,两个焦点分别为和,椭圆G上一点到和的距离之和为12.圆:的圆心为点.

(1)求椭圆G的方程

(2)求的面积

(3)问是否存在圆包围椭圆G?请说明理由.

[解析](1)设椭圆G的方程为：　 ()半焦距为c;

　　　　 则 , 解得 ,

　　 所求椭圆G的方程为：. 　 　　　　　

(2 )点的坐标为

(3)若，由可知点(6，0)在圆外，

　 　若，由可知点(-6，0)在圆外；

　　 不论K为何值圆都不能包围椭圆G.

18.(本小题满分13分)

随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;

(2)计算甲班的样本方差

(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.

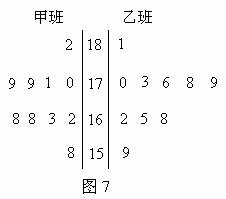
[解析](1)由茎叶图可知：甲班身高集中于之间，而乙班身高集中于 之间。因此乙班平均身高高于甲班;

　　　 (2)

　　　 甲班的样本方差为

　 ＝57

　 (3)设身高为176cm的同学被抽中的事件为A；

　 从乙班10名同学中抽中两名身高不低于173cm的同学有：(181，173)　 (181，176)

　(181，178) (181，179) (179，173) (179，176) (179，178)　 (178，173)

　 (178,　 176)　　 (176，173)共10个基本事件，而事件A含有4个基本事件；

　 　；

17.(本小题满分13分)

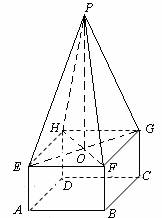
某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P－EFGH,下半部分是长方体ABCD－EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.

(1)请画出该安全标识墩的侧(左)视图;

(2)求该安全标识墩的体积

(3)证明:直线BD平面PEG

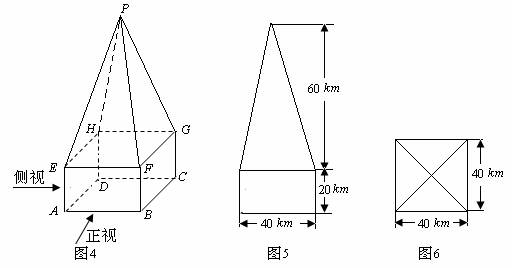
[解析](1)侧视图同正视图,如下图所示.

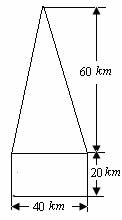
　　(2)该安全标识墩的体积为：

　　(3)如图,连结EG,HF及 BD，EG与HF相交于O,连结PO.

　　　　　 由正四棱锥的性质可知,平面EFGH ,　

　　　　　 又　 平面PEG

　　　　　 又　　 平面PEG；　 　　　　　

16.(本小题满分12分)

已知向量与互相垂直，其中

(1)求和的值

(2)若，,求的值

[解析](1),,即

又∵,　 ∴,即,∴

又　,

(2) ∵

　　, ,即

　又 　, ∴ 　 　　　　　

(二)选做题(14、15题，考生只能从中选做一题)

14．(坐标系与参数方程选做题)若直线(t为参数)与直线垂直，则常数=　　　 .

[答案]

[解析]将化为普通方程为,斜率,

当时,直线的斜率,由得;

当时,直线与直线不垂直.

综上可知,.

15.(几何证明选讲选做题)如图3，点A、B、C是圆O上的点，且AB=4，，则圆O的面积等于　　　 . 　 　　　　　

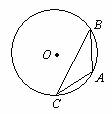
　　　 图3

[答案]

[解析]连结AO,OB,因为 ,所以,为等边三角形,故圆O的半径,圆O的面积.　

(一)必做题(11－13题)

11.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示：

队员i	1	2	3	4	5	6
三分球个数

　图1是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，则图中判断框应填　　　 　，输出的s=　　　

(注：框图中的赋值符号“=”也可以写成“←”或“：=”)

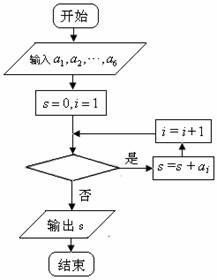
　　　　　 图1

[答案],

[解析]顺为是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图，所图中判断框应填，输出的s=.

12．某单位200名职工的年龄分布情况如图2，现要从中抽取40名职工作样本，用系统抽样法，将全体职工随机按1－200编号，并按编号顺序平均分为40组(1－5号，6－10号…，196－200号).若第5组抽出的号码为22，则第8组抽出的号码应是　　 。若用分层抽样方法，则40岁以下年龄段应抽取　　　 人.

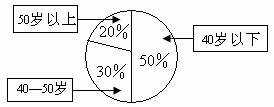
　　　　　　　　 图 2

[答案]37,　 20

[解析]由分组可知,抽号的间隔为5,又因为第5组抽出的号码为22，所以第6组抽出的号码为27，第7组抽出的号码为32，第8组抽出的号码为37.

　　 40岁以下年龄段的职工数为,则应抽取的人数为人.

13．以点(2，)为圆心且与直线相切的圆的方程是　　　　 .

[答案]

[解析]将直线化为,圆的半径,所以圆的方程为 　 　　　　　

10．广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行，各城市之间的路线距离(单位：百公里)见下表.若以A为起点，E为终点，每个城市经过且只经过一次，那么火炬传递的最短路线距离是

A.　　　 B.21　　 C.22　　 D.23

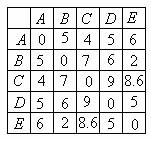
[答案]B

[解析]由题意知,所有可能路线有6种:

①,②,③,④,⑤,⑥,

其中, 路线③的距离最短, 最短路线距离等于,

故选B.

9．函数是

A．最小正周期为的奇函数　　 B. 最小正周期为的偶函数

C. 最小正周期为的奇函数　　 D. 最小正周期为的偶函数

[答案]A

[解析]因为为奇函数,,所以选A.

8.函数的单调递增区间是

A. 　　　B.(0,3)　 C.(1,4)　　 D. 　 　　　　　

[答案]D

[解析],令,解得,故选D

7.已知中，的对边分别为a,b,c若a=c=且，则b=

A.2　　　　 B．4+　　　 C．4-　　 D．

[答案]A

[解析]

由a=c=可知,,所以,

由正弦定理得,故选A