1．抛物线y²＝ax(a≠0)的焦点到其准线的距离是　　　　　　　　　　　　　　 (　)

A.　　　　　B.　　　　　　　 C．|a| 　　　　　　　D．－

解析：由已知焦点到准线的距离为p＝.

答案：B

21.(本小题满分14分)已知等差数列{a_n}的前n项和为S_n且满足a₂＝3，S₆＝36.

(1)求数列{a_n}的通项公式；

(2)若数列{b_n}是等比数列且满足b₁+b₂＝3，b₄+b₅＝24.设数列{a_n·b_n}的前n项和为T_n，求T_n.

解：(1)∵数列{a_n}是等差数列，

∴S₆＝3(a₁+a₆)＝3(a₂+a₅)＝36.

∵a₂＝3，∴a₅＝9，∴3d＝a₅－a₂＝6，∴d＝2，

又∵a₁＝a₂－d＝1，∴a_n＝2n－1.

(2)由等比数列{b_n}满足b₁+b₂＝3，b₄+b₅＝24，

得＝q³＝8，∴q＝2，

∵b₁+b₂＝3，∴b₁+b₁q＝3，∴b₁＝1，b_n＝2^n－1，

∴a_n·b_n＝(2n－1)·.

∴T_n＝1×1+3×2+5×2²+…+(2n－3)·+(2n－1)·，

则2T_n＝1×2+3×2²+5×2³+…+(2n－3)·+(2n－1)·2ⁿ，

两式相减得(1－2)T_n＝1×1+2×2+2×2²+…+2·2^n－2+2·－(2n－1)·2ⁿ，即

－T_n＝1+2(2¹+2²+…+2)－(2n－1)·2ⁿ

＝1+2(2ⁿ－2)－(2n－1)·2ⁿ＝(3－2n)·2ⁿ－3，

∴T_n＝(2n－3)·2ⁿ+3.

20.(本小题满分13分)已知数列{a_n}的每一项都是正数，满足a₁＝2且a－a_na_n+1－2a＝0；等差数列{b_n}的前n项和为T_n，b₂＝3，T₅＝25.

(1)求数列{a_n}、{b_n}的通项公式；

(2)比较++…+与2的大小；

解：(1)由a－a_na_n+1－2a＝0，

得(a_n+1－2a_n)(a_n+1+a_n)＝0，

由于数列{a_n}的每一项都是正数，∴a_n+1＝2a_n，∴a_n＝2ⁿ.

设b_n＝b₁+(n－1)d，由已知有b₁+d＝3,5b₁+d＝25，

解得b₁＝1，d＝2，∴b_n＝2n－1.

(2)由(1)得T_n＝n²，∴＝，

当n＝1时，＝1＜2.

当n≥2时，＜＝－.

∴++…+＜1+－+－+…+－＝2－＜2.

19.(本小题满分12分)用分期付款的方式购买一批总价为2300万元的住房，购买当天首付300万元，以后每月的这一天都交100万元，并加付此前欠款的利息，设月利率为1%，若从首付300万元之后的第一个月开始算分期付款的第1个月，问分期付款的第10个月应付多少万元？全部贷款付清后，买这批住房实际支付多少万元？

解：购买时付款300万元，则欠款2000万元，依题意分20次付清，

则每次交付欠款的数额顺次构成数列{a_n}，

故a₁＝100+2000×0.01＝120(万元)，

a₂＝100+(2000－100)×0.01

＝119(万元)，

a₃＝100+(2000－100×2)×0.01

＝118(万元)，

a₄＝100+(2000－100×3)×0.01

＝117(万元)，

…

a_n＝100+[2000－100(n－1)]×0.01＝120－(n－1)

＝121－n(万元)(1≤n≤20，n∈N^*).

因此{a_n}是首项为120，公差为－1的等差数列.

故a₁₀＝121－10＝111(万元)，

a₂₀＝121－20＝101(万元)，

20次分期付款的总和为

S₂₀＝＝＝2210(万元).

∴实际要付300+2210＝2510(万元).

即分期付款第10个月应付111万元；全部贷款付清后，买这批住房实际支付2510万元.

18.(本小题满分12分)(2010·苏北三市联考)已知数列{a_n}是等差数列，a₂＝3，a₅＝6，数列{b_n}的前n项和是T_n，且T_n+b_n＝1.

(1)求数列{a_n}的通项公式与前n项的和M_n；

(2)求数列{b_n}的通项公式.

解：(1)设{a_n}的公差为d，则：a₂＝a₁+d，a₅＝a₁+4d.

∴a₁＝2，d＝1

∴a_n＝2+(n－1)＝n+1.M_n＝na₁+d＝.

(2)证明：当n＝1时，b₁＝T₁，

由T₁+b₁＝1，得b₁＝.

当n≥2时，∵T_n＝1－b_n，T_n－1＝1－b_n－1，

∴T_n－T_n－1＝(b_n－1－b_n)，

即b_n＝(b_n－1－b_n).

∴b_n＝b_n－1.

∴{b_n}是以为首项，为公比的等比数列.

∴b_n＝·()^n－1＝.

17.(本小题满分12分)已知数列{a_n}满足：a₁＝，a₂＝，a_n+1＝2a_n－a_n－1(n≥2，n∈N^*)，数列{b_n}满足b₁＜0,3b_n－b_n－1＝n(n≥2，n∈N^*)，数列{b_n}的前n项和为S_n.

(1)求数列{a_n}的通项a_n；

(2)求证：数列{b_n－a_n}为等比数列.

解：(1)证明∵2a_n＝a_n+1+a_n－1(n≥2，n∈N^*)，

∴{a_n}是等差数列.

又∵a₁＝，a₂＝，∴a_n＝+(n－1)·＝，

(2)证明：∵b_n＝b_n－1+(n≥2，n∈N^*)，

∴b_n+1－a_n+1＝b_n+－＝b_n－

＝(b_n－)＝(b_n－a_n).

又∵b₁－a₁＝b₁－≠0，

∴{b_n－a_n}是以b₁－为首项，以为公比的等比数列.

16.(本小题满分12分)已知{a_n}是一个等差数列，且a₂＝1，a₅＝－5.

(1)求数列{a_n}的通项a_n；

(2)求{a_n}前n项和S_n的最大值.

解：(1)设{a_n}的公差为d，

由已知条件得，

所以a_n＝a₁+(n－1)d＝－2n+5.

(2)S_n＝na₁+d＝－n²+4n＝4－(n－2)².

所以n＝2时，S_n取到最大值4.

15.等差数列{a_n}的前n项和为S_n，且a₄－a₂＝8，a₃+a₅＝26.记T_n＝，如果存在正整数M，使得对一切正整数n，T_n≤M都成立，则M的最小值是　　.

解析：∵{a_n}为等差数列，由a₄－a₂＝8，a₃+a₅＝26，

可解得S_n＝2n²－n，

∴T_n＝2－，若T_n≤M对一切正整数n恒成立，则只需T_n的最大值≤M即可.

又T_n＝2－<2，∴只需2≤M，故M的最小值是2.

答案：2

14.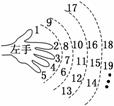“欢欢”按如图所示的规则练习数数，记在数数过程中对应中指的数依次排列所构成的数列为{a_n}，则数到2 008时对应的指头是　　，数列{a_n}的通项公式a_n＝　　.(填出指头的名称，各指头的名称依次为大拇指、食指、中指、无名指、小指).

解析：注意到数1,9,17,25，…，分别都对应着大拇指，且1+8×(251－1)＝2 001，因此数到2 008时对应的指头是食指.对应中指的数依次是：3,7,11,15，…，因此数列{a_n}的通项公式是a_n＝3+(n－1)×4＝4n－1.

答案：食指　4n－1

13.已知数列{a_n}满足＝(n∈N^*)，且a₁＝1，则a_n＝　　.

解析：由已知得＝，

＝，…＝，a₁＝1，

左右两边分别相乘得

a_n＝1·····…···

＝

答案：