10．某公司租地建仓库，每月土地占用费y₁与仓库到车站的距离成反比，而每月库存货物的运费y₂与仓库到车站的距离成正比，如果在距离车站10 km处建仓库，这两项费用y₁和y₂分别为2万元和8万元，那么，要使这两项费用之和最小，仓库应建在离车站　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　)

A．5 km处 　　　B．4 km处　　　　　 C．3 km处 　　　　　　D．2 km处

解析：由题意可设y₁＝，y₂＝k₂x，

∴k₁＝xy₁，k₂＝，

把x＝10，y₁＝2与x＝10，y₂＝8分别代入上式得k₁＝20，k₂＝0.8，

∴y₁＝，y₂＝0.8x(x为仓库与车站距离)，

费用之和y＝y₁+y₂＝0.8x+≥2 ＝8，

当且仅当0.8x＝，即x＝5时等号成立．

答案：A

第Ⅱ卷　(非选择题，共100分)

9．已知函数f(x)满足：f(p+q)＝f(p)f(q)，f(1)＝3，

则+++

等于　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．36　 　　B．24　　　　 C．18 　　　　D．12

解析：由f(p+q)＝f(p)f(q)，

令p＝q＝n，得f²(n)＝f(2n)．

原式＝+++

＝2f(1)+++

＝8f(1)＝24.

答案：B

8．(2010·淄博模拟)若f(a)＝(3m－1)a+b－2m，当m∈[0,1]时f(a)≤1恒成立，则a+b的最大值为　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　)

A.　 　　　　B.　　　　　　 C.　 　　　　　　D.

解析：设g(m)=f(a)=(3a-2)m+b-a，由于当m∈[0,1]时

g(m)=f(a)=(3a-2)m+b-a≤1恒成立，于是

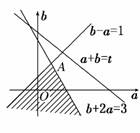
满足此不等式组的点(a，b)构成图中的阴影部分，

其中A()，设a+b=t，显然直线a+b=t过点

A时，t取得最大值.

答案：D

7．已知函数f(x)＝ax²+bx+c的图象过点(－1,3)和(1,1)，若0＜c＜1，则实数a的取值范围是　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　(　)

A．[2,3] 　　　　B．[1,3]　　　　　　 C．(1,2) 　　　　　　D．(1,3)

解析：由题意：得b＝－1，∴a+c＝2.

又0＜c＜1，∴0＜2－a＜1，∴1＜a＜2.

答案：C

6．已知实数a，b，则“ab≥2”是“a²+b²≥4”的　　　　　　　　　　　　 　(　)

A．充分不必要条件　　　　　 　B．必要不充分条件

C．充要条件 　　　　　　　　　D．既不充分也不必要条件

解析：当ab≥2时，a²+b²≥2ab≥4，故充分性成立，而a²+b²≥4时，当a＝－1，b＝3时成立，但ab＝－3＜2，显然ab≥2不成立，故必要性不成立．

答案：A

5．给出下面类比推理命题(其中Q为有理数集，R为实数集，C为复数集)：

①“若a，b∈R，则a－b＝0⇒a＝b”类比推出“若a，b∈C，则a－b＝0⇒a＝b”；

②“若a，b，c，d∈R，则复数a+bi＝c+di⇒a＝c，b＝d”类比推出“若a，b，c，d∈Q，则a+b＝c+d⇒a＝c，b＝d”；

③“若a，b∈R，则a－b＞0⇒a＞b”类比推出“若a，b∈C，则a－b＞0⇒a＞b”．

其中类比得到的结论正确的个数是　　　　　　　　　　　　　　　　　　　 (　)

A．0　 　　　　　　B．1 　　　　　　C．2 　　　　　　　　D．3

解析：①②是正确的，③是错误的，因为复数不能比较大小，如a＝5+6i，b＝4+6i，虽然满足a－b＝1＞0，但复数a与b不能比较大小．

答案：C

4．若集合A＝{x||2x－1|＜3}，B＝{x|＜0}，则A∩B是　　　　　　　　　 (　)

A．{x|－1＜x＜－或2＜x＜3}　　　　 B．{x|2＜x＜3}

C．{x|－＜x＜2}　　　　　　　　　 　D．{x|－1＜x＜－}

解析：∵|2x－1|＜3，∴－3＜2x－1＜3.∴－1＜x＜2.

又∵＜0，∴(2x+1)(x－3)＞0，

∴x＞3或x＜－.∴A∩B＝{x|－1＜x＜－}．

答案：D

3．已知函数f(x)＝，若f(x)≥1，则x的取值范围是　　　　　　 (　)

A．(－∞，－1]　 　　　　　　　B．[1，+∞)

C．(－∞，0]∪[1，+∞) 　　　　D．(－∞，－1]∪[1，+∞)

解析：将原不等式转化为：或，从而得x≥1或x≤－1.

答案：D

2．下列命题中的真命题是　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．若a＞b，c＞d，则ac＞bd　 　　　B．若|a|＞b，则a²＞b²

C．若a＞b，则a²＞b²　 　　　　　　D．若a＞|b|，则a²＞b²

解析：由a＞|b|，可得a＞|b|≥0⇒a²＞b².

答案：D

1．不等式(x+1)≥0的解集是　　　　　　　　　　　　　　　　　　　　 (　)

A．{x|x＞1}　　　　B．{x|x≥1}

C．{x|x≥1或x＝－1} 　　　D．{x|x≥－1或x＝1}

解析：∵≥0，∴x≥1.

同时x+1≥0，即x≥－1.∴x≥1.

答案：B