19． (本小题满分12分)在一个盒子中，放有标号分别为1,2,3的三张卡片，现从这个盒子中有放回地先后抽得两张卡片的标号分别为x、y，记z＝|x－2|+|y－x|.求z的所有可能的取值，并求出z取相应值时的概率．

解：z的所有可能取值为0,1,2,3.

当z＝0时，只有x＝2，y＝2这一种情况，

当z＝1时，有x＝1，y＝1或x＝2，y＝1或x＝2，y＝3或x＝3，y＝3四种情况，

当z＝2时，有x＝1，y＝2或x＝3，y＝2两种情况，

当z＝3时，有x＝1，y＝3或x＝3，y＝1两种情况，

∵有放回地抽两张卡片的所有情况有9种．

∴P(z＝0)＝，P(z＝1)＝，P(z＝2)＝，

P(z＝3)＝.

18． (本小题满分12分)投掷一个质地均匀的、每个面上标有一个数字的正方体玩具，它的六个面中，有两个面标的数字是0，两个面标的数字是2，两个面标的数字是4，将此玩具连续抛掷两次，以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标．

(1)求点P落在区域C：x²+y²≤10内的概率；

(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M，在区域C上随机撒一粒豆子，求豆子落在区域M上的概率．

解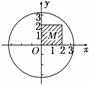：(1)点P的坐标有：(0,0)，(0,2)，(0,4)，(2,0)，(2,2)，(2,4)，(4,0)，　

(4,2)，(4,4)，共9种，其中落在区域C：x²+y²≤10上的点P的坐标有：

(0,0)，(0,2)，(2,0)，(2,2)，共4种．故点P落在区域C：x²+y²≤10内 的

概率为.

(2)区域M为一边长为2的正方形，其面积为4，区域C的面积为10π，则豆子落在区域M上的概率为.

17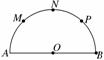．(本小题满分12分)如图，已知AB是半圆O的直径，AB＝8，M、N、　

P是将半圆圆周四等分的三个分点．

(1)从A、B、M、N、P这5个点中任取3个点，求这3个点组成直角

三角形的概率；

(2)在半圆内任取一点S，求三角形SAB的面积大于8的概率．

解：(1)从A、B、M、N、P这5个点中任取3个点，一共可以组成10个三角形：ABM、ABN、ABP、AMN、AMP、ANP、BMN、BMP、BNP、MNP，其中是直角三角形的只有ABM、ABN、ABP 3个，

所以这3个点组成直角三角形的概率P＝.

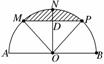
(2)连结MP，取线段MP的中点D，则OD⊥MP，

易求得OD＝2，

当S点在线段MP上时，S_△ABS=×2×8=8，

所以只有当S点落在阴影部分时，三角形SAB面积才能大于8，而

S_阴影=S_扇形OMP-S_△OMP=××4²-×4²=4π-8，

所以由几何概型公式得三角形SAB的面积大于8的概率P=

16．(本小题满分12分)设A＝{(x，y)|1≤x≤6,1≤y≤6，x，y∈N^*}．

(1)求从A中任取一个元素是(1,2)的概率；

(2)从A中任取一个元素，求x+y≥10的概率；

解：(1)设从A中任取一个元素是(1,2)的事件为B，则P(B)＝，所以从A中任取一个元素是(1,2)的概率为.

(2)设从A中任取一个元素，x+y≥10的事件为C，则有(4,6)，(6,4)，(5,5)，(5,6)，(6,5)，(6,6)共6种情况，

于是P(C)＝，

所以从A中任取一个元素，x+y≥10的概率为.

15．已知中心在原点，焦点在x轴上的双曲线的一条渐近线为mx－y＝0，若m在集合{1,2,3,4,5,6,7,8,9}中任意取一个值，使得双曲线的离心率大于3的概率是________．

解析：由题意知m＝，e＝，仅当m＝1或2时，1<e<3，∴e>3时的概率P＝.

答案：

14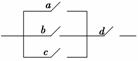． 如图所示，a，b，c，d是四处处于断开状态的开关，任意将其中两个闭合，则电路被接通的概率为　　.

解析：上个开关任意闭合2个，有ab、ac、ad、bc、bd共6种方案，　　

电路被接通的条件是：①开关d必须闭合；②开关a，b，c中有一个闭合即电路被接通有ad、bd和cd共3种方案，所以所求的概率是

答案：

13．如图，在矩形ABCD中，AB=5，AD=7.现在向该矩形内随机投一点P，则　

∠APB>90°时的概率为　　.

解析：P=

答案：

12．在平面直角坐标系xOy中，设D是横坐标与纵坐标的绝对值均不大于2的点构成的区域，E是到原点的距离不大于1的点构成的区域，向D中随机投一点，则所投的点落在E中的概率是__________．

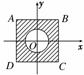解析：如图：区域D表示边长为4的正方形ABCD的内部(含边界)，区域E表示单位圆及其内部，因此P=

答案：

11．若A、B为一对对立事件，其概率分别为P(A)＝，P(B)＝，则x+y的最小值为________．

解析：由已知得+＝1(x>0，y>0)，

∴x+y＝(x+y)(+)

＝5+(+)≥9.

答案：9

10．若－1≤a≤1，－1≤b≤1，则方程x²+2ax+b²＝0有实根的概率等于　　 (　)

A.　　　　　　　 　B.　　　　　　　　　　　　 C. 　　　　　　　D.

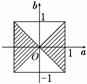解析：方程x²+2ax+b²=0有实根时，应有4a²-4b²≥0，即|a|≥|b|，当-1≤a　　

≤1，-1≤b≤1时，(a，b)对应的区域是一个正方形，满足|a|≥|b|的(a，b)

对应的区域是如图所示的阴影部分，画出图形可得：P=

答案：A

第Ⅱ卷　(非选择题，共100分)