
7.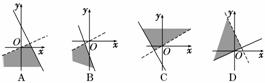 设x、y均是实数,i是虚数单位,复数+i的实部大于0,虚部不小于0,则复数z=x+yi在复平面上的点集用阴影表示为下图中的
( )
设x、y均是实数,i是虚数单位,复数+i的实部大于0,虚部不小于0,则复数z=x+yi在复平面上的点集用阴影表示为下图中的
( )
解析:因为+i=+i,
所以由题意得

画出不等式组表示的平面区域即可知应选A.
答案:A
6.已知向量p=(2,x-1),q=(x,-3),且p⊥q,若由x的值构成的集合A满足A⊇{x|ax=2},则实数a构成的集合是 ( )
A.{0} B.{} C.∅ D.{0,}
解析:∵p⊥q,∴2x-3(x-1)=0,
即x=3,∴A={3}.又{x|ax=2}⊆A,
∴{x|ax=2}=∅或{x|ax=2}={3},
∴a=0或a=,
∴实数a构成的集合为{0,}.
答案:D
5.在△ABC中,D为BC的中点,已知 =a,
=a, =b,则在下列向量中与
=b,则在下列向量中与 同向的
同向的
向量是 ( )
A.+ B.- C. D.|a|a+|b|b
解析:是a+b的单位向量,a+b与向量是 同向.
同向.
答案:C
4.设i,j是平面直角坐标系(坐标原点为O)内分别与x轴、y轴正方向相同的两个单位向量,且 =4i+2j,
=4i+2j, =3i+4j,则△OAB的面积等于
( )
=3i+4j,则△OAB的面积等于
( )
A.15 B.10 C.7.5 D.5
解析:由已知:A(4,2),B(3,4).
则 =12+8=20,|
=12+8=20,| |=2,|
|=2,| |=5.
|=5.
∴
∴
∴

答案:D
3.设P1(2,-1),P2(0,5),且P在P1P2的延长线上,使| |=2|
|=2| |,则点P为( )
|,则点P为( )
A.(-2,11) B.(,3) C.(,3) D.(2,-7)
解析:由题意知 =
= ,
,
设P(x,y),则(-2,6)=(x,y-5),
∴ ∴
∴
∴点P的坐标为(-2,11).
答案:A
2.有下列四个命题:
①(a·b)2=a2·b2; ②|a+b|>|a-b|;③|a+b|2=(a+b)2; ④若a∥b,则a·b=|a|·|b|.
其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
解析:①(a·b)2=|a|2·|b|2·cos2〈a,b〉
≤|a|2·|b|2=a2·b2;
②|a+b|与|a-b|大小不确定;
③正确;
④a∥b,则a=λb(λ∈R),∴a·b=λ·b2,
而|a|·|b|=|λ|·|b|·|b|=|λ|b2,
∴④不正确.
答案:A
1.设z=1+i(i是虚数单位),则+z2= ( )
A.-1-i B.-1+I C.1-i D.1+i
解析:+z2=+(1+i)2=+1+i2+2i=1+i.
答案:D
21.(本小题满分14分)某工厂有工人1 000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(1)A类工人中和B类工人中各抽查多少工人?
(2)从A类工人中的抽查结果和从B类工人中的抽查结果分别如下表1和表2.
表1:
|
生产能 力分组 |
[100,110) |
[110,120) |
[120,130) |
[130,140) |
[140,150) |
|
人数 |
4 |
8 |
x |
5 |
3 |
表2:
|
生产能 力分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150) |
|
人数 |
6 |
y |
36 |
18 |
(i)先确定x,y,再完成下列频率分布直方图,就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组中的数据用该组区间的中点值作代表).
解:(1)A类工人中和B类工人中分别抽查25名和75名.
(2)(ⅰ)由4+8+x+5+3=25,得x=5,
6+y+36+18=75,得y=15.
频率分布直方图如下:
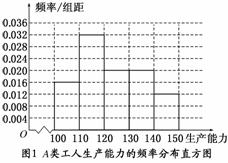
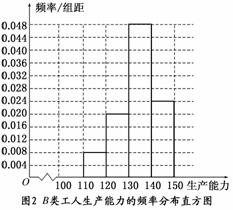
从直方图可以判断:B类工人中个体间的差异程度更小.
(ⅱ)  =
= ×105+
×105+ ×115+
×115+ ×125+
×125+ ×135+
×135+ ×145=123,
×145=123,
 =
= ×115+
×115+ ×125+
×125+ ×135+
×135+ ×145=133.8,
×145=133.8,
 =
= ×123+
×123+ ×133.8=131.1.
×133.8=131.1.
A类工人生产能力的平均数,B类工人生产能力的平均数以及全厂工人生产能力的平均数的估计值分别为123,133.8和131.1.
20.(本小题满分12分)(2009·广东高考)根据空气质量指数API(为整数)的不同,可将空气质量分级如下表:
|
API |
0-50 |
51-100 |
101-150 |
151-200 |
201-250 |
251-300 |
>300 |
|
级别 |
Ⅰ |
Ⅱ |
Ⅲ1 |
Ⅲ2 |
Ⅳ1 |
Ⅳ2 |
Ⅴ |
|
状况 |
优 |
良 |
轻微 污染 |
轻度 污染 |
中度污染 |
中度重 污染 |
重度 污染 |
|
|
 |
 |
 |
 |
 |
对某城市一年(365天)的空气质量进行监测,获得的API数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图.
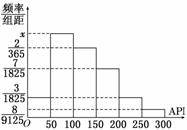
(1)求直方图中x的值;
(2)计算一年中空气质量分别为良和轻微污染的天数.
解:(1)根据频率分布直方图可知,
x=÷50
=.
(2)空气质量为Y的天数=(Y对应的频率÷组距)×组距×365天,
所以一年中空气质量为良和轻微污染的天数分别是
×50×365=119(天)和×50×365=100(天).
0.275+0.100+0.050)×5 000=2 125;
(ii)平均分为:=85×0.025+95×0.050+105×0.200+115×0.300+125×0.275+135×0.100+145×0.050=117.5.
(iii)成绩落在[126,150]中的概率为:P=×0.275+0.10+0.050=0.260.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com