15．(2009·江南测试)棱长为a的正方体ABCD－A₁B₁C₁D₁的8个顶点都在球O的表面上，E、F分别是棱AA₁、DD₁的中点，则直线EF被球O截得的线段长为________．

解析：因为正方体内接于球，所以2R=，R=，

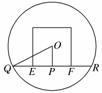
过球心O和点E、F的大圆的截面图如图所示，

则直线被球截得的线段为QR，过点O作OP⊥QR

于点P，所以，在△QPO中，QR=2QP=2

答案：

14．母线长为1的圆锥的侧面展开图的圆心角等于π，则该圆锥的体积为________．

解析：圆锥的侧面展开图扇形的弧长，即底面圆的周长为π·1＝π，于是设底面圆的半径为r，

则有2πr＝π，所以r＝，

于是圆锥的高为h＝＝，

故圆锥的体积为V＝π.

答案：π

13.如图，AD⊥平面BCD，∠BCD＝90°，AD＝BC＝CD＝a，则二面角

C－AB－D的大小为__________．

解析：取BD的中点E，连结CE，则CE⊥面ABD，作EF⊥AB，

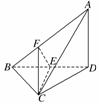∴CF⊥AB得∠CFE为所求．

又CE=a，CF=，

∴sin∠CFE=

答案：60°

12．(2009·辽宁高考)设某几何体的三视图如下(尺寸的长度单位为m)．

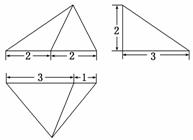
则该几何体的体积为　　m³.

解析：由三视图可知原几何体是一个三棱锥，且三棱锥的高为2，底面三角形的一边长为4，且该边上的高为3，

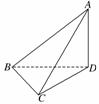故所求三棱锥的体积为V=×2××3×4=4 m³，

答案：4

11．如图，在正方体ABCD－A₁B₁C₁D₁中，P为棱DC的中点，则D₁P与BC₁所在直线所成角的余弦值等于________．

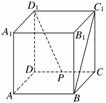
解析：过C₁作D₁P的平行线交DC的延长线于点F，连结BF，则∠BC₁F或其补角等于异面直线D₁P与BC₁所成的角．设正方体的棱长为1，由P为棱DC的中点，则易得BC₁＝，

C₁F＝ ＝，

BF＝ ＝.

在△BC₁F中，cos∠BC₁F＝

＝.

答案：

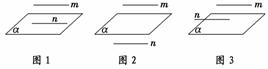
10．已知直线m、n及平面α，其中m∥n，那么在平面α内到两条直线m、n距离相等的点的集合可能是：(1)一条直线；(2)一个平面；(3)一个点；(4)空集．其中正确的是(　)

A．(1)(2)(3)　 　　　　B．(1)(4)　　 C．(1)(2)(4) 　　D．(2)(4)

解析：如图1，当直线m或直线n在平面α内时不可能有符合题意的点；如图2，直线m、n到已知平面α的距离相等且两直线所在平面与已知平面α垂直，则已知平面α为符合题意的点；如图3，直线m、n所在平面与已知平面α平行，则符合题意的点为一条直线，从而选C.

答案：C

第Ⅱ卷　(非选择题，共100分)

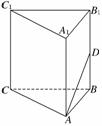
9.如图，在正三棱柱ABC-A₁B₁C₁中，已知AB=1，D在棱BB₁上，且BD=1，则AD与平面AA₁C₁C所成角的正弦值为　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　B.　　　 C.　 　　D.

解析：如图，取C₁A₁、CA的中点E、F，连接B₁E与BF，则B₁E⊥平面CAA₁C₁，

过D作DH∥B₁E，则DH⊥平面CAA₁C₁，连接AH，则∠DAH为所求的

DH=B₁E=，DA=，所以sin∠DAH=

答案：A

8．(2010·皖中模拟)已知三棱锥的三个侧面两两垂直，三条侧棱长分别为4、4、7，若此三棱锥的各个顶点都在同一个球面上，则此球的表面积是　　　　　　　　 (　)

A．81π　 　　　B．36π　　　　 C.　 　　　　　D．144π

解析：补成长方体易求4R²＝81，

∴S＝4πR²＝81π.

答案：A

7．过平行六面体ABCD－A₁B₁C₁D₁任意两条棱的中点作直线，其中与平面DBB₁D₁平行的直线共有　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　(　)

A．4条 　　　　　　B．6条 　　　　　C．12条　　 　　　　　D．8条

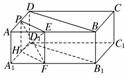解析：如图，P、E、F、H分别为AD、AB、A₁B₁、

A₁D₁的中点，则平面PEFH∥平面DBB₁D₁，所以

四边形PEFH的任意两顶点的连线都平行于平面DBB₁D₁，

共6条，同理在另一侧面也有6条，共12条．

答案：C

6.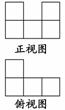用一些棱长是1 cm的小正方体堆放成一个几何体，其正视图和俯视图如图所示，则这个几何体的体积最多是　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．6 cm³ 　　　　　　B．7 cm³

C．8 cm³　 　　　　　D．9 cm³

解析：由正视图与俯视图可知小正方体最多有7块，故体积最多为7 cm³.

答案：B