4.要得到y＝sin(2x－)的图象，只要将y＝sin2x的图象　　　　　　　　　　　 　(　)

A.向左平移个单位　 　　　　　　B.向右平移个单位

C.向左平移个单位　 　　　　　　D.向右平移个单位

解析：∵y＝sin(2x－)＝sin2(x－)，

∴只要将y＝sin2x的图象向右平移个单位便得到y＝sin(2x－)的图象.

答案：D

3.(2010·温州模拟)函数f(x)＝2sin(2x+)在[－，]上对称轴的条数为　　　　　 (　)

A.1 　　　　B.2　　　　　　　 C.3　 　　　　　　　　　D .0

解析：∵当－≤x≤，

∵－≤2x+≤π，

∴函数的对称轴为：2x+＝－，，

∴x＝－，或x＝.

答案：B

2.已知α∈(，π)，sinα＝，则tan(α+)等于　　　　　　　　　　　　　　　　 (　)

A. 　　　　　B.7　　　　　　 C.－ 　　　　　　　　D.－7

解析：由α∈(，π)，sinα＝，得tanα＝－，tan(α+)＝＝.

答案：A

1.集合M＝{x|x＝sin，n∈Z}，N＝{x|x＝cos，n∈N}，则M∩N等于　　　　 (　)

A.{－1,0,1}　　B.{0,1}　　　　　 C.{0} 　　　　　　　D.∅

解析：∵M＝{x|x＝sin，n∈Z}＝{－，0，}，

N＝{－1,0,1}，

∴M∩N＝{0}.

答案：C

21.(2009·东北四市模拟)如图，正四棱柱ABCD－A₁B₁C₁D₁中，AA₁＝2AB＝4，点E在CC₁上，且CE＝λCC₁.

(1)λ为何值时，A₁C⊥平面BED；

(2)若A₁C⊥平面BED，求二面角A₁－BD－E的余弦值.

解：法一：(1)连接B₁C交BE于点F，连接AC交BD于点G，

∴AC⊥BD，由垂直关系得，A₁C⊥BD，

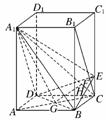若A₁C⊥平面BED，则A₁C⊥BE，

由垂直关系可得B₁C⊥BE，

∴△BCE∽△B₁BC，∴＝＝，

∴CE＝1，∴λ＝＝.

(2)连接A₁G，连接EG交A₁C于H，则A₁G⊥BD.

∵A₁C⊥平面BED，

∴∠A₁GE是二面角A₁－BD－E的平面角.

∵A₁G＝3，EG＝，A₁E＝，

∴cos∠A₁GE＝＝，

法二：(1)以D为坐标原点，射线DA为x轴的正半轴，射线DC为y轴的正半轴，射线DD₁为z轴的正半轴，建立如图所示直角坐标系D－xyz.

依题设，D(0,0,0)，B(2,2,0)，C(0,2,0)，A₁(2,0,4)，

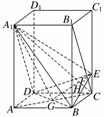∵CE＝λCC₁＝4λ，∴E(0,2,4λ)，

∴＝(2,2,0)，＝(2,0,4)，

＝(－2,2，－4)，＝(0,2,4λ)，

∵·＝2×(－2)+2×2+0×(－4)＝0，

∴⊥，∴DB⊥A₁C.

若A₁C⊥平面BED，则A₁C⊥DE，∴⊥，

∴·＝(－2)×0+2×2+(－4)×4λ＝4－16λ＝0，

∴λ＝.

(2)设向量n＝(x，y，z)是平面DA₁B的一个法向量，

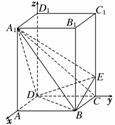则n⊥，n⊥，∴2x+2y＝0,2x+4z＝0，

令z＝1，则x＝－2，y＝2，∴n＝(－2,2,1)

由(1)知平面BDE的一个法向量为＝(－2,2，－4)

∴cos〈n，〉＝＝.

即二面角A₁－BD－E的余弦值为.

.

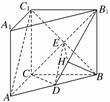
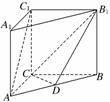
20. (2009·西安八校联考)如图，在直三棱柱ABC－A₁B₁C₁中，AC＝BC＝CC₁＝2，AC⊥BC，D为AB的中点.

(1)求证：AC₁∥平面B₁CD；

(2)求二面角B－B₁C－D的正弦值.

解：(1)证明：如图，连接BC₁交B₁C于点E，

则E为BC₁的中点.

∵D为AB的中点，∴在△ABC₁中，AC₁∥DE

又AC₁⊄平面B₁CD，DE⊂平面B₁CD，

∴AC₁∥平面B₁CD

(2)∵AC＝BC，D为AB的中点，

∴CD⊥AB.又平面ABC⊥平面ABB₁A₁，

∴CD⊥平面ABB₁A₁.

∴平面B₁CD⊥平面B₁BD，

过点B作BH⊥B₁D，垂足为H，则BH⊥平面B₁CD，

连接EH，

∵B₁C⊥BE，B₁C⊥EH，

∴∠BEH为二面角B－B₁C－D的平面角.

在Rt△BHE中，BE＝，BH＝＝，

则sin∠BEH＝＝.

即二面角B－B₁C－D的正弦值为.

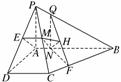
19.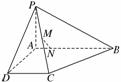 如图所示，四棱锥P－ABCD中，AB⊥AD，AD⊥DC，PA⊥底面ABCD，PA＝AD＝DC＝AB＝1，M为PC的中点，N点在AB上且AN＝NB.

(1)证明：MN∥平面PAD；

(2)求直线MN与平面PCB所成的角.

解：(1)证明：过M作ME∥CD交PD于E，

连接AE.

∵AN＝NB，

∴AN＝AB＝DC＝EM.

又EM∥DC∥AB，∴EMAN，

∴AEMN为平行四边形，

∴MN∥AE，又AE⊂平面PAD，MN⊄平面PAD，

∴MN∥平面PAD.

(2)过N点作NQ∥AP交BP于点Q，NF⊥CB交CB于点F，

连接QF，过N点作NH⊥QF交QF于H，连接MH.

易知QN⊥平面ABCD，∴QN⊥BC，而NF⊥BC，

∴BC⊥平面QNF，

∴BC⊥NH，而NH⊥QF，∴NH⊥平面PBC，

∴∠NMH为直线MN与平面PCB所成的角.

通过计算可得MN＝AE＝，QN＝，NF＝，

∴NH＝＝＝，

∴sin∠NMH＝＝，∴∠NMH＝60°.

∴直线MN与平面PCB所成的角为60°.

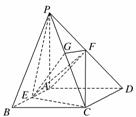
18. (2010·徐州模拟)如图，PA垂直于矩形ABCD所在的平面，AD＝PA＝2，CD＝2，E、F分别是AB、PD的中点.

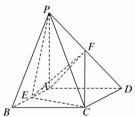
(1)求证：AF∥平面PCE；

(2)求证：平面PCE⊥平面PCD；

(3)求四面体PEFC的体积.

解：(1)证明：设G为PC的中点，连结FG，EG，

∵F为PD的中点，E为AB的中点，

∴FG CD，AECD

∴FG 　AE，∴AF∥GE

∵GE⊂平面PEC，

∴AF∥平面PCE；

(2)证明：∵PA＝AD＝2，∴AF⊥PD

又∵PA⊥平面ABCD，CD⊂平面ABCD，

∴PA⊥CD，∵AD⊥CD，PA∩AD＝A，

∴CD⊥平面PAD，

∵AF⊂平面PAD，∴AF⊥CD.

∵PD∩CD＝D，∴AF⊥平面PCD，

∴GE⊥平面PCD，

∵GE⊂平面PEC，

∴平面PCE⊥平面PCD；

(3)由(2)知，GE⊥平面PCD，

所以EG为四面体PEFC的高，

又GF∥CD，所以GF⊥PD，

EG＝AF＝，GF＝CD＝，

S_△PCF＝PD·GF＝2.

得四面体PEFC的体积V＝S_△PCF·EG＝.

17.已知直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝1，BC＝2，CD＝1+，过A作AE⊥CD，垂足为E，G、F分别为AD、CE的中点，现将△ADE沿AE折叠，使DE⊥EC.

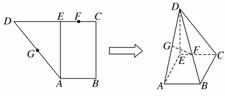
(1)求证：BC⊥平面CDE；

(2)求证：FG∥平面BCD；

(3)求四棱锥D－ABCE的体积.

解：(1)证明：由已知得：

DE⊥AE，DE⊥EC，∴DE⊥平面ABCE.

∴DE⊥BC.又BC⊥CE，CE∩DE＝E，

∴BC⊥平面DCE.

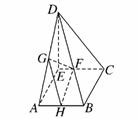
(2)证明：取AB中点H，连结GH，FH，

∴GH∥BD，FH∥BC，

∴GH∥平面BCD，FH∥平面BCD.

又GH∩FH＝H，

∴平面FHG∥平面BCD，

∴FG∥平面BCD(由线线平行证明亦可).

(3)V＝×1×2×＝.

16． (2010·泉州模拟)如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形，俯视图为正方形，侧视图为直角三角形，尺寸如图所示)．

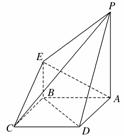
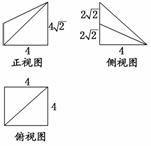
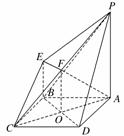
(1)求四棱锥P-ABCD的体积；

(2)证明：BD∥平面PEC；

(3)若G为BC上的动点，求证：AE⊥PG.

解：(1)由几何体的三视图可知，底面ABCD是边长为4的正方形，PA⊥平面ABCD，PA∥EB，且PA＝4，BE＝2，AB＝AD＝CD＝CB＝4，

∴V_P－ABCD＝PA×S_ABCD＝×4×4×4＝.

(2)证明：连结AC交BD于O点，

取PC中点F，连结OF，

∵EB∥PA，且EB＝PA，

又OF∥PA，且OF＝PA，

∴EB∥OF，且EB＝OF，

∴四边形EBOF为平行四边形，

∴EF∥BD.

又EF⊂平面PEC，BD⊄平面PEC，所以BD∥平面PEC.

(3)连结BP，∵＝＝，∠EBA＝∠BAP＝90°，

∴△EBA∽△BAP，∴∠PBA＝∠BEA，

∴∠PBA+∠BAE＝∠BEA+∠BAE＝90°，

∴PB⊥AE.

又∵BC⊥平面APEB，∴BC⊥AE，

∴AE⊥平面PBG，∴AE⊥PG.