14.设△ABC的内角A，B，C所对的边长分别为a，b，c且acosB－bcosA＝c.则的值为　　.

解析：由acosB－bcosA＝c及正弦定理可得sinAcosB－sinBcosA＝sinC，即sinAcosB－sinBcosA＝sin(A+B)，即5(sinAcosB－sinBcosA)＝3(sinAcosB+sinBcosA)，即sinAcosB＝4sinBcosA，因此tanA＝4tanB，所以＝4.

答案：4

13.已知函数f(x)＝2sin(ωx+φ)的图象如下图所示，则f()＝　　.

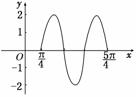
解析：由图象知，函数的周期为×T＝π，

∴T＝.

∵f()＝0，

∴f()＝f(+)

＝f(+)＝－f()＝0.

答案：0

12.已知扇形内切圆半径与扇形半径之比为1∶3，则内切圆面积与扇形面积之比为　　.

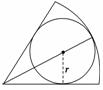解析：如图，设内切圆半径为r，则扇形的半径为3r，计算可

得扇形中心角为，

故S_内切圆∶S_扇形＝πr²∶·3r·(·3r)＝2∶3.

答案：2∶3

11．若函数f(x)＝(1+tanx)cosx,0≤x＜，则f(x)的最大值为________．

解析：f(x)＝(1+tanx)cosx

＝cosx+sinx

＝2sin(x+)，

∵0≤x＜，∴f(x)_max＝2.

答案：2

10.设函数f(x)＝Asin(ωx+φ)，(A≠0，ω＞0，－＜φ＜)的图象关于直线x＝对称，它的周期是π，则　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.f(x)的图象过点(0，)　　　　　 B.f(x)的图象在[，]上递减

C.f(x)的最大值为A　　　　　　　 D.f(x)的一个对称中心是点(，0)

解析：T＝π，∴ω＝2.∵图象关于直线x＝对称，

∴sin(ω+φ)＝±1，

即×2+φ＝+kπ，k∈Z

又∵－<φ<，∴φ＝

∴f(x)＝Asin(2x+).再用检验法.

答案：D

第Ⅱ卷　(非选择题，共100分)

9.函数y＝sin(2x－)在区间[－，π]上的简图是　　　　　　　　　　　　　 (　)

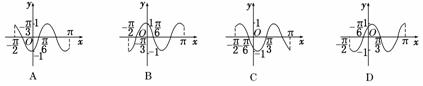
解析：当x＝－时，y＝sin(－π－)

＝sin＝＞0，排除B、D，

当x＝时，y＝sin(－)＝sin0＝0，排除C.

答案：A

8.设集合M＝{平面内的点(a，b)}，N＝{f(x)|f(x)＝acos2x+bsin2x，x∈R}，给出从M到N的映射f：(a，b)→f(x)＝acos2x+bsin2x，则点(1，)的象f(x)的最小正周期为(　)

A.π 　　　　　　B.　　　　　　　 C. 　　　　　　　　　D.

解析：f(x)＝cos2x+sin2x＝2sin(2x+)，则最小正周期为π.

答案：A

7.有一种波，其波形为函数y＝sin(x)的图象，若在区间[0，t]上至少有2个波峰(图象的最高点)，则正整数t的最小值是　　　　　　　　　　　　　　　　　　　　　　 (　)

A.3 　　　　　　　B.4　　　　　　　　 C.5　 　　　　　　D.6

解析：由T＝＝＝4，可知此波形的函数周期为4，显然当0≤x≤1时函数单调递增，x＝0时y＝0，x＝1时y＝1，因此自0开始向右的第一个波峰所对的x值为1，第二个波峰对应的x值为5，所以要区间[0，t]上至少两个波峰，则t至少为5.

答案：C

6.在△ABC中，若sin²A+sin²B－sinAsinB＝sin²C，且满足ab＝4，则该三角形的面积为(　)

A.1 　　　　B.2　　　　　　　　 C. 　　　　　　　　　D.

解析：∵sin²A+sin²B－sinAsinB＝sin²C，

∴a²+b²－ab＝c²，∴cosC＝＝，

∴C＝60°，∴S_△ABC＝absinC＝×4×＝.

答案：D

5.给定函数①y＝xcos(+x)，②y＝1+sin²(π+x)，③y＝cos(cos(+x))中，偶函数的个数

是　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　(　)

A.3 　　　　　　　　B.2　　　　　　　　　 C.1 　　　　　　　　　　　　D.0

解析：对于①y＝xcos(π+x)＝xsinx，是偶函数，故①正确；对于②y＝1+sin²(π+x)＝sin²x+1，是偶函数，故②正确；对于③y＝cos(cos(+x))

＝cos(－sinx)＝cos(sinx)，

∵f(－x)＝cos(sin(－x))＝cos(－sinx)＝cos(sinx)＝f(x)，

∴函数是偶函数，故③正确.

答案：A