
3.如图所给的程序中,输出时A的值是输入时A的值的 ( )
INPUT A A=A+A A=A+AA=2 A PRINT A END |
A.1倍 B.2倍 C.3倍 D.4倍
解析:输出时为4A.
答案:D
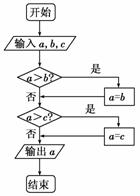
2.如图给出了一个算法程序框图,该算法程序框图的功能是 ( )
A.求a,b,c三数的最大数
B.求a,b,c三数的最小数
C.将a,b,c按从小到大排列
D.将a,b,c按从大到小排列
解析:求a,b,c三个数的最小数.
答案:B
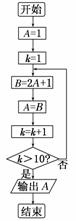
1.执行如图的程序框图,输出的A为 ( )
A.2047 B.2049 C.1023 D.1025
解析:该程序框图的功能是求数列{an}的第11项,而数列{an}满足a1=1,an=2an-1+1,
∵an+1=2an-1+2
∴{an+1}是以2为公式,以2为首项的等比数列.
∴an=2n-1,
∴a11=211-1=2047.
答案:A
第1题图 第2题图
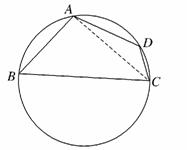
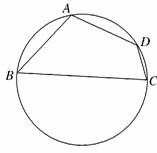
21. (2010·长沙模拟)长沙市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域近似地为半径是R的圆面.该圆面的内接四边形
ABCD是原棚户建筑用地,测量可知边界AB=AD=4万米,
BC=6万米,CD=2万米.
(1)请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值;
(2)因地理条件的限制,边界AD、DC不能变更,而边界AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC上设计一点P;使得棚户区改造的新建筑用 地APCD的面积最大,并求最大值.
解:(1)因为四边形ABCD内接于圆,
所以∠ABC+∠ADC=180°,连接AC,由余弦定理:
 AC2=42+62-2×4×6×cos∠ABC
AC2=42+62-2×4×6×cos∠ABC
=42+22-2×2×4cos∠ADC.
所以cos∠ABC=,∵∠ABC∈(0,π),
故∠ABC=60°.
S四边形ABCD=×4×6×sin60°+×2×4×sin120°
=8(万平方米).
在△ABC中,由余弦定理:
AC2=AB2+BC2-2AB·BC·cos∠ABC
=16+36-2×4×6×.
AC=2.
由正弦定理==2R,
∴2R===,
∴R=(万米).
(2)∵S四边形APCD=S△ADC+S△APC,
又S△ADC=AD·CD·sin120°=2,
设AP=x,CP=y.
则S△APC=xy·sin60°=xy.
又由余弦定理AC2=x2+y2-2xycos60°
=x2+y2-xy=28.
∴x2+y2-xy≥2xy-xy=xy.
∴xy≤28,当且仅当x=y时取等号
∴S四边形APCD=2+xy≤2+×28=9,
∴最大面积为9万平方米.
20.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0)的一系列对应值如下表:
|
x |
 |
 |
 |
 |
 |
 |
 |
|
y |
-1 |
1 |
3 |
1 |
-1 |
1 |
3 |
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果,若函数y=f(kx)(k>0)周期为,当x∈[0,]时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围;
解:(1)设f(x)的最小正周期为T,得
T= -(-)=2π,
由T=,得ω=1.
又
令ω·+φ=,即+φ=,
解得φ=-,
∴f(x)=2sin(x-)+1.
(2)∵函数y=f(kx)=2sin(kx-)+1的周期为,
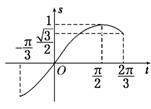 又k>0,∴k=3.
又k>0,∴k=3.
令t=3x-,
∵x∈[0,],
∴t∈[-,]
如图sint=s在[-,]上有两个不同的解的充要条件是s∈[,1),
∴方程f(kx)=m在x∈[0,]时恰好有两个不同的解的充要条件是m∈[+1,3),
 即实数m的取值范围是[+1,3).
即实数m的取值范围是[+1,3).
19.如图,点A,B是单位圆上的两点,A,B点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标
为(,),记∠COA=α.
(1)求的值;
(2)求|BC|2的值.
解:(1)∵A的坐标为(,),根据三角函数的定义可知,
sinα=,cosα=,
∴==.
(2)∵△AOB为正三角形,∴∠AOB=60°.
∴cos∠COB=cos(α+60°)=cosαcos60°-sinαsin60°
=×-×=,
∴|BC|2=|OC|2+|OB|2-2|OC|·|OB|cos∠COB
=1+1-2×=.
18.在△ABC中,A、B为锐角,角A、B、C所对的边分别为a、b、c,且sinA=,sinB=.
(1)求A+B的值;
(2)若a-b=-1,求a、b、c的值.
解:(1)∵A、B为锐角,sinA=,sinB=,
∴cosA==,
cosB==,
∴cos(A+B)=cosAcosB-sinAsinB
=×-×=.
∵0<A+B<π,∴A+B=.
(2)由(1)知C=,∴sinC=.
由正弦定理==得
a=b=c,即a=b,c=b,
∵a-b=-1,∴b-b=-1,∴b=1,
 ∴a=,c=.
∴a=,c=.
17.在△ABC中,角A、B、C所对的边分别是a、b、c,tanA=,cosB=.
(1)求角C;
(2)若△ABC的最短边长是,求最长边的长.
解:(1)∵tanA=,
∴A为锐角,则cosA=,sinA=.
又cosB=,
∴B为锐角,则sinB=,
∴cosC=-cos(A+B)=-cosAcosB+sinAsinB
=-×+×=-.
又C∈(0,π),∴C=π.
(2)∵sinA=>sinB=,
∴A>B,即a>b,
∴b最小,c最大,
由正弦定理得=,
得c=·b=·=5.
16.已知 =(cos+sin,-sin),
=(cos+sin,-sin), =(cos-sin,2cos).
=(cos-sin,2cos).
(1)设f(x)= ·
· ,求f(x)的最小正周期和单调递减区间;
,求f(x)的最小正周期和单调递减区间;
(2)设有不相等的两个实数x1,x2∈,且f(x1)=f(x2)=1,求x1+x2的值.
解:(1)由f(x)= ·
· 得
得
f(x)=(cos+sin)·(cos-sin)+(-sin)·2cos
=cos2-sin2-2sincos
=cosx-sinx
=cos(x+),
所以f(x)的最小正周期T=2π.
又由2kπ≤x+≤π+2kπ,k∈Z,
得-+2kπ≤x≤+2kπ,k∈Z.
故f(x)的单调递减区间是[-+2kπ,+2kπ](k∈Z).
(2)由f(x)=1得cos(x+)=1,故cos(x+)=.
又x∈,于是有x+∈,得x1=0,x2=-,
所以x1+x2=-.
15.下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是π;
②终边在y轴上的角的集合是{α|α=,k∈Z};
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④把函数y=3sin(2x+)的图象向右平移个单位得到y=3sin2x的图象;
⑤函数y=sin(x-)在[0,π]上是减函数.
其中真命题的序号是 .
解析:①y=sin2x-cos2x=-cos2x,故最小正周期为π,①正确;
②k=0时,α=0,则角α终边在x轴上,故②错;
③由y=sinx在(0,0)处切线为y=x,所以y=sinx与y=x的图象只有一个交点,故③错;
④y=3sin(2x+)的图象向右平移个单位得到
y=3sin[2(x-)+]=3sin2x,故④正确;
⑤y=sin(x-)=-cosx在[0,π]上为增函数,故⑤错.
综上,①④为真命题.
答案:①④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com