10．(2009·天津高考)设抛物线y²＝2x的焦点为F，过点M(，0)的直线与抛物线相交于A、B两点，与抛物线的准线相交于点C，|BF|＝2，则△BCF与△ACF的面积之比＝　　　　　　　　　　　　　　

(　)

A. 　　　　　　　B.　　　　　　　　　　 C. 　　　　　　　　　D.

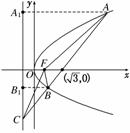解析：如图过A、B作准线l：x= -的垂线，垂足分别为A₁，B₁，

由于F到直线AB的距离为定值．

∴＝.

又∵△B₁BC∽△A₁AC.

∴＝，

由拋物线定义＝＝.

由|BF|＝|BB₁|＝2知x_B＝，y_B＝－，

∴AB：y－0＝(x－)．

把x＝代入上式，求得y_A＝2，x_A＝2，

∴|AF|＝|AA₁|＝.

故＝＝＝.

答案：A

第Ⅱ卷　(非选择题，共100分)

9．(2009·四川高考)已知双曲线－＝1(b>0)的左、右焦点分别为F₁、F₂，其一条渐近线方程为y＝x，点P(，y₀)在该双曲线上，则·＝　　　　　　　　　　 (　)

A．－12　 　　　　　　　B．－2　　　　　　　 C．0　　　　 　D．4

解析：由渐近线方程y＝x得b＝，

点P(，y₀)代入－＝1中得y₀＝±1.

不妨设P(，1)，∵F₁(2,0)，F₂(－2,0)，

∴·＝(2－，－1)·(－2－，－1)

＝3－4+1＝0.

答案：C

8．(2009·全国卷Ⅱ)双曲线－＝1的渐近线与圆(x－3)²+y²＝r²(r>0)相切，则r＝(　)

A.　 　　　　　　B．2　　　　　 　C．3 　　　　　　　D．6

解析：双曲线的渐近线方程为y＝±x即x±y＝0，圆心(3,0)到直线的距离d＝＝.

答案：A

7．抛物线y＝－4x²上的一点M到焦点的距离为1，则点M的纵坐标是　　　 (　)

A. 　　　　　　　B.　　　　　 　　　C．－ 　　　　　D．－

解析：准线方程为y＝，

由定义知－y_M＝1⇒y_M＝－.

答案：C

6．双曲线－＝1(a>0，b>0)的一条渐近线方程为y＝x(e为双曲线离心率)，则有(　)

A．b＝2a　 　　　　B．b＝a　　　　　 C．a＝2b　 　　　　　D．a＝b

解析：由已知＝e，

∴＝×，∴c＝b，又a²+b²＝c²，

∴a²+b²＝5b²，∴a＝2b.

答案：C

5．△ABC的顶点A(－5,0)，B(5,0)，△ABC的内切圆圆心在直线x＝3上，则顶点C的轨迹方程是　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　(　)

A.－＝1　 　　　　　　　　　B.－＝1

C.－＝1(x＞3) 　　　　　　　D.－＝1(x＞4)

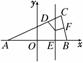
解析：如图|AD|＝|AE|＝8，|BF|＝|BE|＝2，|CD|＝|CF|，

所以|CA|－|CB|＝8－2＝6.

根据双曲线定义，所求轨迹是以A、B为焦点，实轴长为6的双曲线的右支，方程为－＝1(x＞3)．

答案：C

4．若直线ax+2by－2＝0(a＞0，b＞0)始终平分圆x²+y²－4x－2y－8＝0的周长，则+的最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1 　　　　　　　B．5　　　　　　　　　 C．4 　　　　　　D．3+2

解析：由(x－2)²+(y－1)²＝13，得圆心(2,1)，

∵直线平分圆的周长，即直线过圆心．

∴a+b＝1.

∴+＝(+)(a+b)＝3++≥3+2，

当且仅当＝，即a＝－1，b＝2－时取等号，

∴+的最小值为3+2.

答案：D

3．已知双曲线－＝1的离心率为e，抛物线x＝2py²的焦点为(e,0)，则p的值为(　)

A．2 　　　　　　　B．1　　　　　　　 C. 　　　　　　　D.

解析：依题意得e＝2，抛物线方程为y²＝x，故＝2，得p＝.

答案：D

2．过点A(4，a)与B(5，b)的直线与直线y＝x+m平行，则|AB|＝　　　　　　　　　 (　)

A．6　 　　　　　　B.　　　　　　　 C．2 　　　　　　D．不确定

解析：由题知＝1，∴b－a＝1.

∴|AB|＝＝.

答案：B

1．抛物线y²＝ax(a≠0)的焦点到其准线的距离是　　　　　　　　　　　　　　 (　)

A.　　　　　B.　　　　　　　 C．|a| 　　　　　　　D．－

解析：由已知焦点到准线的距离为p＝.

答案：B