19．已知函数f(x)＝ax²+4(a为非零实数)，设函数F(x)＝.

(1)若f(－2)＝0，求F(x)的表达式；

(2)设mn＜0，m+n＞0，试判断F(m)+F(n)能否大于0?

解：(1)由f(－2)＝0,4a+4＝0⇒a＝－1，

∴F(x)＝

(2)∵，∴m，n一正一负．

不妨设m＞0且n＜0，则m＞－n＞0，

F(m)+F(n)＝f(m)－f(n)＝am²+4－(an²+4)

＝a(m²－n²)，

当a＞0时，F(m)+F(n)能大于0，

当a＜0时，F(m)+F(n)不能大于0.

18． (2010·吉林模拟)沪杭高速公路全长166千米．假设某汽车从上海莘庄镇进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶到杭州．已知该汽车每小时的运输成本y(以元为单元)由可变部分和固定部分组成：可变部分与速度v(千米/时)的平方成正比，比例系数为0.02；固定部分为200元．

(1)把全程运输成本y(元)表示为速度v(千米/时)的函数，并指出这个函数的定义域；

(2)汽车应以多大速度行驶才能使全程运输成本最小？最小运输成本为多少元？

解：(1)依题意得：y＝(200+0.02v²)×

＝166(0.02v+)(60≤v≤120)．

(2)y＝166(0.02v+)≥166×2

＝664(元)

当且仅当0.02v＝即v＝100千米/时时取等号．

答：当速度为100千米/时时，最小的运输成本为664元．

17．若a₁＞0，a₁≠1，a_n+1＝(n＝1,2，…)

(1)求证：a_n+1≠a_n；

(2)令a₁＝，写出a₂、a₃、a₄、a₅的值，观察并归纳出这个数列的通项公式a_n.

解：(1)证明：(采用反证法)．若a_n+1＝a_n，

即＝a_n，解得a_n＝0,1.

从而a_n＝a_n－1＝…＝a₂＝a₁＝0,1，与题设a₁＞0，a₁≠1相矛盾，

故a_n+1≠a_n成立．

(2)a₁＝、a₂＝、a₃＝、a₄＝、a₅＝，a_n＝，

n∈N^*.

16．已知f(x)＝－3x²+a(6－a)x+b.

(1)解关于a的不等式f(1)＞0；

(2)当不等式f(x)＞0的解集为(－1,3)时，求实数a，b的值．

解：(1)f(1)＝－3+a(6－a)+b＝－a²+6a+b－3，

∵f(1)＞0，∴a²－6a+3－b＜0.

Δ＝24+4b，当Δ≤0

即b≤－6时，f(1)＞0的解集为∅；

当b＞－6时，3－＜a＜3+，

∴f(1)＞0的解集为{a|3－＜a＜3+}．

(2)∵不等式－3x²+a(6－a)x+b＞0的解集为(－1,3)，

∴解之，得

15．已知点P(a，b)与点Q(1,0)在直线2x－3y+1＝0的两侧，则下列说法正确的是________．

①2a－3b+1＞0；

②a≠0时，有最小值，无最大值；

③∃M∈R⁺，使＞M恒成立；

④当a＞0且a≠1，b＞0时，则的取值范围为(－∞，－)∪(，+∞)．

解析：由已知(2a－3b+1)(2－0+1)＜0，

即2a－3b+1＜0，∴①错；

当a＞0时，由3b ＞2a+1，

可得＞+，

∴不存在最小值，∴②错；

表示为(a，b)与(0,0)两点间的距离，由线性规划知识可得：

＞＝恒成立，

∴③正确；

表示为(a，b)和(1,0)两点的斜率．

由线性规划知识可知④正确．

答案：③④

14．某公司租赁甲、乙两种设备生产A，B两类产品，甲种设备每天能生产A类产品5件和B类产品10件，乙种设备每天能生产A类产品6件和B类产品20件．已知设备甲每天的租赁费为200元，设备乙每天的租赁费为300元，现该公司至少要生产A类产品50件，B类产品140件，所需租赁费最少为________元．

解析：设需租赁甲种设备x台，乙种设备y台，

则

目标函数为z＝200x+300y.

作出其可行域，易知当x＝4，y＝5时，z＝200x+300y有最小值2300元．

答案：2300

13．关于x的不等式ax²+4x－1≥－2x²－a恒成立，那么实数a的取值范围是________．

解析：不等式ax²+4x－1≥－2x²－a

可化为(a+2)x²+4x+a－1≥0，

当a+2＝0，即a＝－2时，不恒成立，不合题意．

当a+2≠0时，要使不等式恒成立，

需解得a≥2.

所以a的取值范围为[2，+∞)．

答案：[2，+∞)

12．关于x的不等式x²+(a+1)x+ab＞0的解集是{x|x＜－1或x＞4}，则实数a、b的值分别为________．

解析：由不等式的解集为{x|x＜－1或x＞4}可得，－1,4是方程x²+(a+1)x+ab＝0的两根，

∴，解得a＝－4，b＝1.

答案：－4,1

11．不等式组，所表示的平面区域的面积等于________．

解析：不等式组表示的平面区域如图所示，由

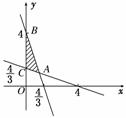
得交点A的坐标为(1,1)．又B、C两点的坐标为(0,4)，

(0，)．故S_△ABC＝(4－)×1＝.

答案：

10．某公司租地建仓库，每月土地占用费y₁与仓库到车站的距离成反比，而每月库存货物的运费y₂与仓库到车站的距离成正比，如果在距离车站10 km处建仓库，这两项费用y₁和y₂分别为2万元和8万元，那么，要使这两项费用之和最小，仓库应建在离车站　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　(　)

A．5 km处 　　　B．4 km处　　　　　 C．3 km处 　　　　　　D．2 km处

解析：由题意可设y₁＝，y₂＝k₂x，

∴k₁＝xy₁，k₂＝，

把x＝10，y₁＝2与x＝10，y₂＝8分别代入上式得k₁＝20，k₂＝0.8，

∴y₁＝，y₂＝0.8x(x为仓库与车站距离)，

费用之和y＝y₁+y₂＝0.8x+≥2 ＝8，

当且仅当0.8x＝，即x＝5时等号成立．

答案：A

第Ⅱ卷　(非选择题，共100分)