8. 在(x²－)ⁿ的展开式中，常数项为15，则n＝　　　　　　　　　　 (　)

A．3 　　　　　　B．4　　　　　　　　　 C．5　 　　　　D．6

解析：对于二项式的展开式问题，关键要考虑通项，第k+1项T_k+1＝C ·(－)^k＝C应有2n－3k＝0，∴n＝，而n是正整数，故k＝2,4,6….结合题目给的已知条件，常数项为15，验证可知k＝4，n＝6.

答案：D

7．在区域内任取一点P，则点P落在单位圆x²+y²＝1内的概率为(　)

A.　 　　　　　　　　B.　　　　　　　　 C.　 　　　　　　　　D.

解析：区域为△ABC内部(含边界)，则概率为

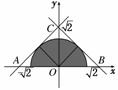P=

答案：D

6.从数字0,1,2,3,5,7,8,11中任取3个分别作为Ax+By+C＝0中的A，B，C(A，B，C互不相等)的值，所得直线恰好经过原点的概率为　　　　　　　　　　　　　 (　)

A. 　　　　　　　　　B.　　　　　　　　 C. 　　　　　　　D.

解析：P＝＝.

答案：B

5．(2009·重庆高考)⁸的展开式中x⁴的系数是　　　　　　　　　　　 (　)

A．16　 　　　　　B．70　　　　　 C．560　 　　　　　　　D．1 120

解析：由二项展开式通项公式得T_k+1＝C(x²) ^k＝2^kC.由16－3k＝4，得k＝4，则x⁴的系数为2⁴C＝1 120.

答案：D

4．(2009·辽宁高考)从5名男医生、4名女医生中选3名医生组成一个医疗小分队，要求其中男、女医生都有，则不同的组队方案共有　　　　　　　　　　　　　 (　)

A．70种 　　　　　B．80种　　　　　　 C．100种　　 　　　　D．140种

解析：分恰有2名男医生和恰有1名男医生两类，从而组队方案共有：C×C+C×C＝70种．

答案：A

3.某班级要从4名男生、2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案种数为　　　　　　　　　　　　　　　　　　　 (　)

A．14 　　　　　　B．24　　　　　　　 C．28　 　　　　　D．48

解析：法一：4人中至少有1名女生包括1女3男及2女2男两种情况，故不同的选派方案种数为

C·C+C·C＝2×4+1×6＝14.

法二：从4男2女中选4人共有C种选法，4名都是男生的选法有C种，故至少有1名女生的选派方案种数为C－C＝15－1＝14.

答案：A

2．有四个游戏盘，如果撒一粒黄豆落在阴影部分，则可中奖，小明希望中奖，他应当选择的游戏盘为　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　(　)

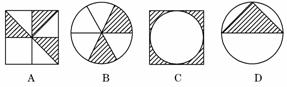
解析：A游戏盘的中奖概率为，B游戏盘的中奖概率为，C游戏盘的中奖概率为，D游戏盘的中奖概率为 ，A游戏盘的中奖概率最大．

答案：A

1．把红桃、黑桃、方块、梅花四张纸牌随机发给甲、乙、丙、丁四个人，每人分得一张，事件“甲分得梅花”与事件“乙分得梅花”是　　　 　　　　　　　　　　　(　)

A．对立事件　　　　　　　 　B．不可能事件

C．互斥但不对立事件　　 　　　　　D．以上答案均不对

解析：四张纸牌分发给四人，每人一张，甲和乙不可能同时分得梅花，所以是互斥事件，但也有可能丙或丁分得梅花，故不是对立事件．

答案：C

21．已知函数f(x)＝ax－－2lnx，f(1)＝0.

(1)若函数f(x)在其定义域内为单调函数，求a的取值范围；

(2)若函数f(x)的图象在x＝1处的切线的斜率为0，且a_n+1＝f′()－n²+1，已知a₁＝4，求证：a_n≥2n+2.

解：(1)因为f(1)＝a－b＝0，所以a＝b，

所以f(x)＝ax－－2lnx，

所以f′(x)＝a+－.

要使函数f(x)在定义域(0，+∞)内为单调函数，

则在(0，+∞)内f′(x)恒大于等于0或恒小于等于0.

当a＝0时，则f′(x)＝－＜0在(0，+∞)内恒成立；适合题意．

当a＞0时，要使f′(x)＝a(－)²+a－≥0恒成立，则a－≥0，解得a≥1；

当a＜0时，由f′(x)＝a+－＜0恒成立，适合题意．

所以a的取值范围为(－∞，0]∪[1，+∞)．

(2)根据题意得：f′(1)＝0，即a+a－2＝0，得a＝1，

所以f′(x)＝(－1)²，

于是a_n+1＝f′()－n²+1＝(a_n－n)²－n²+1

＝a－2na_n+1.

用数学归纳法证明如下：

当n＝1时，a₁＝4＝2×1+2，

当n＝2时，a₂＝9＞2×2+2；

假设当n＝k(k≥2且k∈N^*)时，不等式a_k＞2k+2成立，即a_k－2k＞2成立，

则当n＝k+1时，a_k+1＝a_k(a_k－2k)+1＞(2k+2)×2+1＝4k+5＞2(k+1)+2，

所以当n＝k+1，不等式也成立，

综上得对所有n∈N^*时，都有a_n≥2n+2.

20．某工艺品加工厂准备生产具有收藏价值的奥运会标志--“中国印·舞动的北京”和奥运会吉祥物--“福娃”．该厂所用的主要原料为A、B两种贵金属，已知生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒，生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒．若奥运会标志每套可获利700元，奥运会吉祥物每套可获利1200元，该厂月初一次性购进原料A、B的量分别为200盒和300盒．问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大？最大利润为多少？

解：设该厂每月生产奥运会标志和奥运会吉祥物分别为x，y套，月利润为z元，

由题意得

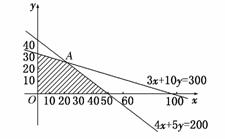
目标函数为z＝700x+1200y.

作出二元一次不等式组所表示的平面区域，即可行域，如图：

目标函数可变形为y＝－x+，

∵－＜－＜－，

∴当y＝x+通过图中的点A时，最大，z最大．解得点A坐标为(20,24)．

将点A(20,24)代入z＝700x+1200y

得z_max＝700×20+1200×24＝42800元．

答：该厂生产奥运会标志和奥运会吉祥物分别为20、24套时月利润最大，最大利润为42800元．