
19.用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.
(1)求恰有两个区域用红色鲜花的概率;
(2)记花圃中红色鲜花区域的块数为X,求X的分布列及其数学期望.
解:(1)设M表示事件“恰有两个区域用红色鲜花”,如图,当区域A、D同色时,共有5×4×3×1×3=180种;
当区域A、D不同色时,共有5×4×3×2×2=240种;
|
A |
||
|
B |
C |
E |
|
D |
因此,所有基本事件总数为:180+240=420种.
它们是等可能的.
又因为A、D为红色时,共有4×3×3=36种;
B、E为红色时,共有4×3×3=36种;
因此,事件M包含的基本事件有:36+36=72种.
所以,恰有两个区域用红色鲜花的概率P(M)==.
(2)随机变量X的取值分别为0,1,2.
则当X=0时,用黄、蓝、白、橙四种颜色来涂色,
若A、D为同色时,共有4×3×2×1×2=48种;
若A、D为不同色时,共有4×3×2×1×1=24种;
即X=0所包含的基本事件有48+24=72种,
所以P(X=0)==;
由第(1)问得P(X=2)=;
所以P(X=1)=1--=.
从而随机变量X的分布列为:
|
X |
0 |
1 |
2 |
|
P |
|
|
|
所以,E(X)=0×+1×+2×=1.
18.某车间准备从10名工人中选配4人到某生产线工作,为了安全生产,工厂规定:一条生产线上熟练工人数不得少于3人.已知这10名工人中有熟练工8名,学徒工2名.
(1)求工人的配置合理的概率;
(2)为了督促其安全生产,工厂安全生产部门每月对工人的配备情况进行两次抽检,求两次检验得到的结果不一致的概率.
解:(1)一条生产线上熟练工人数不得少于3人有C+CC种选法.工人的配置合理的
概率=.
(2)两次检验是相互独立的,可视为独立重复试验,因两次检验得出工人的配置合理的概率均为,故“两次检验得出的结果不一致”即两次检验中恰有一次是合格的概率为C(1-)=.
17.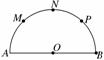 如图,已知AB是半圆O的直径,AB=8,M、N、
P是将半圆圆周
如图,已知AB是半圆O的直径,AB=8,M、N、
P是将半圆圆周
四等分的三个分点.
(1)从A、B、M、N、P这5个点中任取3个点,求这3个点组成直角
三角形的概率;
(2)在半圆内任取一点S,求三角形SAB的面积大于8的概率.
解:(1)从A、B、M、N、P这5个点中任取3个点,一共可以组成10个三角形:ABM、ABN、ABP、AMN、AMP、ANP、BMN、BMP、BNP、MNP,其中是直角三角形的只有ABM、ABN、ABP 3个,
 所以这3个点组成直角三角形的概率P=.
所以这3个点组成直角三角形的概率P=.
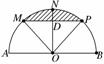
(2)连结MP,取线段MP的中点D,则OD⊥MP,
易求得OD=2,
当S点在线段MP上时,S△ABS= ×2
×2 ×8=8
×8=8 ,
,
所以只有当S点落在阴影部分时,三角形SAB面积才能大于8 ,而
,而
S阴影=S扇形OMP-S△OMP= ×
× ×42-
×42- ×42=4π-8,
×42=4π-8,
所以由几何概型公式得三角形SAB的面积大于8 的概率P=
的概率P=
16.设A={(x,y)|1≤x≤6,1≤y≤6,x,y∈N*}.
(1)求从A中任取一个元素是(1,2)的概率;
(2)从A中任取一个元素,求x+y≥10的概率;
(3)设Y为随机变量,Y=x+y,求E(Y).
解:(1)设从A中任取一个元素是(1,2)的事件为B,则P(B)=,所以从A中任取一个元素是(1,2)的概率为.
(2)设从A中任取一个元素,x+y≥10的事件为C,则有(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)共6种情况,
于是P(C)=,
所以从A中任取一个元素,x+y≥10的概率为.
(3) Y可能取的值为2,3,4,5,6,7,8,9,10,11,12.
P(Y=2)=,P(Y=3)=,P(Y=4)=,
P(Y=5)=,P(Y=6)=,P(Y=7)=,
P(Y=8)=,P(Y=9)=,P(Y=10)=,
P(Y=11)=,P(Y=12)=.
则E(Y)=2×+3×+4×+5×+6×+7×+8×+9×+10×+11×+12×=7.
15.已知中心在原点,焦点在x轴上的双曲线的一条渐近线为mx-y=0,若m在集合{1,2,3,4,5,6,7,8,9}中任意取一个值,使得双曲线的离心率大于3的概率是________.
解析:由题意知m=,e=,仅当m=1或2时,1<e<3,∴e>3时的概率P=.
答案:
14.(2010·安徽师大附中模拟)a= (sinx+cosx)dx则二项式(a-)6展开式中含x2的项的系数是________.
(sinx+cosx)dx则二项式(a-)6展开式中含x2的项的系数是________.
解析:a= (sinx+cosx)dx=(sinx-cosx)
(sinx+cosx)dx=(sinx-cosx) 

=(sinπ-cosπ)-(sin0-cos0)
=(0+1)-(0-1)=2.
又∵Tr+1=C(a) (-)r
(-)r
=C  (-1)r
(-1)r =C
=C  (-1)r
(-1)r .
.
由3-r=2,解r=1,
∴x2项的系数为-Ca5=-192.
答案:-192
12.在平面直角坐标系xOy中,设D是横坐标与纵坐标的绝对值均不大于2的点构成的区域,E是到原点的距离不大于1的点构成的区域,向D中随机投一点,则所投的点落在E中的概率是__________.
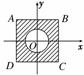 解析:如图:区域D表示边长为4的正方形ABCD的内部(含边界),区域E表示单位圆及其内部,因此P=
解析:如图:区域D表示边长为4的正方形ABCD的内部(含边界),区域E表示单位圆及其内部,因此P=
答案:
13(2009·广东高考)已知离散型随机变量X的分布列如下表.若E(X)=0,D(X)=1,则a=________,b=________.
|
X |
-1 |
0 |
1 |
2 |
|
P |
a |
b |
c |
|
解析:由题意
解得a=,b=c=.
答案:
11.若A、B为一对对立事件,其概率分别为P(A)=,P(B)=,则x+y的最小值为________.
解析:由已知得+=1(x>0,y>0),
∴x+y=(x+y)(+)
=5+(+)≥9.
答案:9
10.若从数字0,1,2,3,4,5中任取三个不同的数作为二次函数y=ax2+bx+c的系数,则与x轴有公共点的二次函数的概率是 ( )
A. B. C. D.
解析:若从0,1,2,3,4,5中任选三个数作为二次函数的系数,对应二次函数共有CA=100个,其中与x轴有公共点的二次函数需满足b2≥4ac,当c=0时,a,b只需从1,2,3,4,5中任选2个数字即可,对应的二次函数共有A个,当c≠0时,若b=3,此时满足条件的(a,c)取值有(1,2),(2,1)有2种情况;当b=4时,此时满足条件的(a,c)取值有(1,2),(1,3),(2,1),(3,1)有4种情况;当b=5时,此时满足条件的(a,c)取值有(1,2),(1,3),(1,4),(2,3),(2,1),(3,1),(4,1),(3,2)有8种情况,即共有20+2+4+8=34种情况满足题意,故其概率为=.
答案:A
第Ⅱ卷 (非选择题,共100分)
9.口袋中有4个白球,n个红球,从中随机地摸出两个球,这两个球颜色相同的概率大于0.6,则n的最小值为 ( )
A.13 B.14 C.15 D.16
解析:由已知条件可得>0.6,
解之得n>12或n<1(舍去),∴n的最小值为13.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com