
9.组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是 ( )
A.57.2,3.6 B.57.2,56.4 C.62.8,63.6 D.62.8,3.6
解析:设这组数据分别为x1,x2,…,xn,则=(x1+x2+…+xn)=i,方差为s2=[(x1-)2+…+(xn-)2]=(xi-)2,每一组数据都加60后,
′=(xi+60)=i+60=+60=62.8,
方差s′2=(xi+60-′)2=s2=3.6.
答案:D
8.中考试以后,班长算出了全班40个人数学成绩的平均分为M.如果把M当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均值为N,那么M∶N为
( )
A. B.1 C. D.2
解析:设40个人的数学总分为z,则z=40M且z=41N-M,由40M=41N-M得M=N.
答案:B
7.2010·银川模拟)某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成五组,并绘制频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65 kg属于偏胖,低于55 kg属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05,第二小组的频数为400,则该校高三年级的男生总数和体重正常的频率分别为 ( )
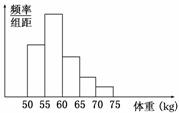
A.1 000,0.50 B.800,0.50 C.800,0.60 D.1 000,0.60
解析:由题知第二小组的频率为1-(0.25+0.20+0.10+0.05)=0.40,又频数为400,故总人数为1 000,体重正常的频率为0.4+0.2=0.60.
答案:D
4.4-4.5间的频数为100×0.1×0.3=3.
又前4组的频数成等比数列,∴公比为3.
根据后6组频数成等差数列,且共有100-13=87人.
从而4.6-4.7间的频数最大,且为1×33=27,∴a=0.27,
设公差为d,则6×27+d=87.
∴d=-5,从而b=4×27+(-5)=78.
答案:A
6为了考察两个变量x和y之间的线性相关性,甲、乙两位同学各自独立作了10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1、l2,已知两人所得的试验数据中,变量x和y的数据的平均值都相等,且分别都是s、t,那么下列说法正确的是( )
A.直线l1和l2一定有公共点(s,t)
B.直线l1和l2相交,但交点不一定是(s,t)
C.必有l1∥l2
D.l1与l2必定重合
解析:线性回归直线方程为=x+.而=-,
即=t-s,t=s+.
∴(s,t)在回归直线上.
∴直线l1和l2一定有公共点(s,t).
答案:A
4.3-4.4间的频数为100×0.1×0.1=1.
3.某校数学教研组为了解学生学习数学的情况,采用分层抽样的方法从高一600人、高二680人、高三720人中,抽取50人进行问卷调查,则高一、高二、高三抽取的人数分别是 ( )
A.15,16,19 B.15,17,18 C.14,17,19 D.15,16,20
解析:分层抽样要求每层中每个个体被抽到的概率均相等,据题意中每个个体被抽到的概率为=,故高一、高二和高三分别被抽取的人数为600×=15,680×=17,720×=18.
答案:B
4对于给定的两个变量的统计数据,下列说法正确的是 ( )
A.都可以分析出两个变量的关系
B.都可以用一条直线近似地表示两者的关系
C.都可以作出散点图
D.都可以用确定的表达式表示两者的关系
解析:给出一组样本数据,总可以作出相应的散点图,但不一定能分析出两个变量的关系,更不一定符合线性相关或有函数关系.
答案:C
5为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为 ( )
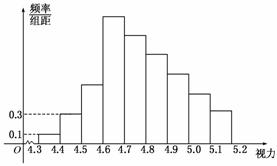
A.0.27,78 B.0.27,83 C.2.7,78 D.2.7,83
解析:由频率分布直方图知组矩为0.1.
2.如图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为 ( )
A.304.6 B.303.6 C.302.6 D.301.6
解析:由已知得平均数
=
=303.6.
答案:B
1.某地区共有10万户居民,该地区城市住户与农村住户之比为4∶6,根据分层抽样方法,调查了该地区1 000户居民冰箱拥有情况,调查结果如下表所示,那么可以估计该地区农村住户中无冰箱的总户数约为 ( )
|
|
城市 |
农村 |
|
有冰箱 |
356(户) |
440(户) |
|
无冰箱 |
44(户) |
160(户) |
A.1.6万户 B.4.4万户 C.1.76万户 D.0.24万户
解析:由分层抽样按比例抽取可得×100 000=16 000.
 答案:A
答案:A
21.一个口袋里有2个红球和4个黄球,从中随机地连取3个球,每次取一个,记事件A=“恰有一个红球”,事件B=“第3个是红球”.
求:(1)不放回时,事件A、B的概率;
(2)每次抽后放回时,A、B的概率.
解:(1)由不放回抽样可知,第一次从6个球中取一个,第二次只能从5个球中取一个,第三次从4个球中取一个,基本事件共6×5×4=120个,又事件A中含有基本事件3×2×4×3=72个,(第一个是红球,则第2,3个是黄球,取法有2×4×3种,第2个是红球和第3个是红球取法一样多),
∴P(A)==.
第3次取到红球对前两次没有什么要求,
因为红球数占总球数的,每一次取到都是随机地等可能事件,
∴P(B)=.
(2)由放回抽样知,每次都是从6个球中取一个,有取法63=216种,事件A含基本事件3×2×4×4=96种.
∴P(A)==.
第三次抽到红球包括B1={红,黄,红},B2={黄,黄,红},B3={黄,红,红},B4={红,红,红}四种两两互斥的情形,P(B1)==,P(B2)==,
P(B3)==,
P(B4)==,
∴P(B)=P(B1)+P(B2)+P(B3)+P(B4)
=+++=.
20.(2009·陕西高考)某食品企业一个月内被消费者投诉的次数用X表示.据统计,随机变量X的概率分布如列下:
(1)求a的值和X的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
|
X |
0 |
1 |
2 |
3 |
|
P |
0.1 |
0.3 |
2a |
a |
解:(1)由概率分布的性质有0.1+0.3+2a+a=1,
解得a=0.2.
∴X的概率分布列为
|
X |
0 |
1 |
2 |
3 |
|
P |
0.1 |
0.3 |
0.4 |
0.2 |
∴E(X)=0×0.1+1×0.3+2×0.4+3×0.2=1.7.
(2)设事件A表示“两个月内共被投诉2次”;事件A1表示“两个月内有一个月被投诉2次,另外一个月被投诉0次”;事件A2表示“两个月内每个月均被投诉1次”.
则由事件的独立性得
P(A1)=CP(X=2)P(X=0)=2×0.4×0.1=0.08,
P(A2)=[P(X=1)]2=0.32=0.09,
∴P(A)=P(A1)+P(A2)=0.08+0.09=0.17.
故该企业在这两个月内共被消费者投诉2次的概率为0.17.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com