2．　 特点：a=恒量．

1．　 定义：在相等的时间内速度的变化相等的直线运动叫做匀变速直线运动．　　

4、匀速运动的基本规律应用

　 [例7]一辆实验小车可沿水平地面(图中纸面)上的长直轨道匀速向右运动。有一台发出细光束的激光器装在小转台M上，到轨道的距离MN为d=10m，如所示。转台匀速运动，使激光束在水平面内扫描，扫描一周的时间为T=60s。光束转动方向如图中箭头所示。当光束与MN的夹角为45⁰时，光束正好射到小车上。如果再经过Δt=2．5s光速又射到小车上，问小车的速度为多少？(结果保留二位数字)

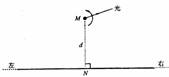　 解析：在Δt内，光束转过角度Δα= Δt/T×360⁰=15⁰根据题意，有两种可能，光束照到小车时，小车正在从左侧接近N点，第二种可能是小车正在从右侧远离N点。

　 接近N点时，在Δt内光束与MN夹角从45⁰变为30⁰，小车走过 L_l，速度应为：V₁= L₁／Δt=d(tg45⁰－tg30⁰)/Δt＝1．7m／s．

　　 远离 N点时，V₂= L₂／Δt= d(tg60⁰一tg45⁰)／Δt，

　　 V₂＝2．9m／s

[例8]天文观测表明，几乎所有远处的恒星(或星系)都在以各自的速度背离我们运动，离我们最远的星体，背离我们运动的速度(成为退行速度)越大。也就是说，宇宙在膨胀，不同星体的退行速度v和星体与我们的距离r成正比，即v＝Hr。式中H为一常量，称为哈勃常数，已由天文观察测定。

　　 为解释上述现象，有人提出一种理论，认为宇宙是从一个大爆炸的火球开始形成的。假设大爆炸后各星体即以不同的速度向外做匀速运动，并设想我们就位于其中心，则速度越大的星体现在离我们越远．这一结果与上述天文观测一致。

　　 由上述理论和天文观测结果，可估算宇宙年龄t，其计算式为t＝　　　　。根据近期观测，哈勃常数H＝3×10^-2m/(s·ly)(ly表示“光年”：光在一年中行进的距离)，由此估算宇宙的年龄约为　　Y(Y表示“年”)。

　　 [解析]根据题目提供的宇宙大爆炸理论，认为宇宙是从一个大爆炸的火球开始形成的假设大爆炸后各星体即以不同的速度向外做匀速运动(想象礼花爆炸时的情景)，并设想我们就位于中心，那么宇宙的年龄就是星体远离我们的运动时间。

　　 解：星体远离我们的运动时间就是宇宙的年龄，由匀速运动公式可得：t＝r／v，天文观察结果：v＝Hr。所以t＝

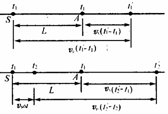[例9]如图所示，声源S和观察A都沿x轴正方向运动，相对于地面的速率分别为V_s和v_A，空气中声音传播的速率为v_P，设V_s＜v_P,v', v_A＜v_P，空气相对于地面没有流动．

　(1)若声源相继发出两个声信号，时间间隔为Δt，请根据发出的这两个声信号从声源传播到观察者的过程，确定观察者接收到这两个声信号的时间间隔Δt^/．

　 (2)请利用(1)的结果，推导此情形下观察者接收到的声波频率与声源发出的声波频率间的关系式．

解析：(1)设t₁、t₂为声源发出两个信号的时刻，t₁^/、t₂^/为观察者接收到两个信号的时刻，则第一个信号经过时间(t₁^/－t₁)被观察者A接收到，第二个信号经过时间(t₂^/－t₂)被观察者A接收到，且

(t₂－t₁)=Δt，(t₂^/－t₁^/)=Δt^/。

设声源发出第一个信号时，S、A两点间的距离为L，则两个声信号从声源传播到观察者的过程中，它们运动的距离关系如图所示，可得：

V_P(t₁^/－t₁)=L+V_A(t₁^/－t₁)，

V_P(t₂^/－t₂)=L+V_A(t₂^/－t₁)－V_SΔt，　　　 由以上各式得

(2)设声源发出声波的振动周期为T，则由以上结论观察者接收到声波振动的周期^/为，由此得观察者接收到的声波频率与声源发出的声波频率间的关系式

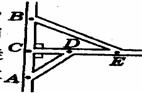[例10]图为某郊区部分道路图，一歹徒在A地作案后乘车沿AD道路逃窜，警方同时接到报警信息，并立即由B地乘警车沿道路BE拦截。歹徒到达D点后沿DE道路逃窜，警车．恰好在E点追上了歹徒。已知警方与歹徒车辆行驶的速度均为 60 km/h， AC＝4 km， BC= 6 km，DE＝5 km。则歹徒从A地逃窜至E点被抓获共用时(　 B　 )

　　 A． 12min　　 　B． 10min　　 C． 8min　　　　 D． 6min

[解析]∵两者速度相等，且运动时间相等，故s_警＝s_歹　

∴BE＝AD+DE，即＝+DE，代入数据，解方程得　 CD= 3 km　 t＝s/v＝10min　　

　　　　　 匀变速直线运动

基础知识　 一、匀变速直线运动

3、充分注意矢量的方向性

[例6]物体在恒力F₁作用下，从A点由静止开始运动，经时间t到达B点。这时突然撤去F₁，改为恒力F₂作用，又经过时间2t物体回到A点。求F₁、F₂大小之比。

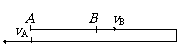解：设物体到B点和返回A点时的速率分别为v_A、v_B， 利用平均速度公式可以得到v_A和v_B的关系。再利用加速度定义式，可以得到加速度大小之比，从而得到F₁、F₂大小之比。

　　 画出示意图如右。设加速度大小分别为a₁、a₂，有：

　　 ∴a₁∶a₂=4∶5，∴F₁∶F₂=4∶5

说明：特别要注意速度的方向性。平均速度公式和加速度定义式中的速度都是矢量，要考虑方向。本题中以返回A点时的速度方向为正，因此AB段的末速度为负。

　　 注意：平均速度和瞬时速度的区别。平均速度是运动质点的位移与发生该位移所用时间的比值，它只能近似地描述变速运动情况，而且这种近似程度跟在哪一段时间内计算平均速度有关。平均速度的方向与位移方向相同。瞬时速度是运动物体在某一时刻(或某一位置)的速度。某时刻的瞬时速度，可以用该时刻前后一段时间内的平均速度来近似地表示。该段时间越短，平均速度越近似于该时刻的瞬时速度，在该段时间趋向零时，平均速度的极限就是该时刻的瞬时速度。

2、明确位移与路程的关系

[例3]关于路程与位移，下列说法中正确的是(　 )

　　 A．位移的方向就是质点运动的方向　　 B．路程等于位移的大小

　　 C．位移的值不会比路程大　　 D．质点运动的位移为零时，其运动的路程也为零

解析：位移是从始点到终点的有向线段，路程是实际轨迹的总长度，所以位移总不会大于路程．只有物体在AS一直线上做方向不变的直线运动时，位移的大小才等于路程．　　 答案：c

说明：位移和路程的区别与联系。位移是矢量，是由初始位置指向终止位置的有向线段；路程是标量，是物体运动轨迹的总长度。一般情况位移的大小不等于路程，只有当物体作单向直线运动时路程才等于位移的大小。

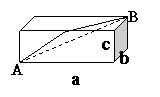[例4]一实心的长方体，三边长分别是a、b、c(a＞b＞c)，如图所示．有一质点，从顶点A沿表面运动到长方体的对角B，求：(1)质点的最短路程．(2)质点的位移大小．

解析：沿表面的运动轨迹与A、B的连线构成直角三角形时路程小于钝角三角形时．

　　 答案(1)(2)s=

[例5]在与x轴平行的匀强电场中，一带电量q=1.0×10^-8C、质量m=2.5×10^-3kg的物体在光滑水平面上沿着x轴作直线运动，其位移与时间的关系是x＝0.16t－0.02t²，式中x以m为单位，t以s为单位。从开始运动到5s末物体所经过的路程为　　　　 m，克服电场力所做的功为　　　　 J。

解：须注意：本题第一问要求的是路程；第二问求功，要用到的是位移。

将x＝0.16t－0.02t²和对照，可知该物体的初速度v₀=0.16m/s，加速度大小a=0.04m/s²，方向跟速度方向相反。由v₀=at可知在4s末物体速度减小到零，然后反向做匀加速运动，末速度大小v₅=0.04m/s。前4s内位移大小，第5s内位移大小，因此从开始运动到5s末物体所经过的路程为0.34m，而位移大小为0.30m，克服电场力做的功W=mas₅=3×10^-5J。

3、速度、速度变化、加速度的关系：

①方向关系：加速度的方向与速度变化的方向一定相同。在直线运动中，若a的方向与V₀的方向相同，质点做加速运动；若a的方向与V₀的方向相反，质点做减速运动。

②大小关系：V、△V、a无必然的大小决定关系。

规律方法　 　1、灵活选取参照物

[例1]甲、乙两辆汽车以相同的恒定速度直线前进，甲车在前，乙车在后，甲车上的人A和乙车上的人B各用石子瞄准对方，以相对自身为v₀的初速度 同时水平射击对方，若不考虑石子的竖直下落，则

A、A先被击中；　　　 B、B先被击中；　 C、两同时被击中；　　 D、可以击中B而不能击中A；

解析：由于两车都以相同而恒的速度运动，若以车为参照物，则两石子做的是速度相同的匀速运动，故应同时被击中，答案C

说明：灵活地选取参照物，以相对速度求解有时会更方便。

[例2]如图所示，在光滑的水平地面上长为L的木板B的右端放一小物体A，开始时A、B静止。同时给予A、B相同的速率v₀，使A向左运动，B向右运动，已知A、B相对运动的过程中，A的加速度向右，大小为a₁，B的加速度向左，大小为a₂，a₂<a₁，要使A滑到B的左端时恰好不滑下，v₀为多少？

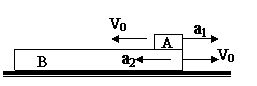解析：A滑到B左端恰不滑下即A、B相对静止，选取B为参照物，A对B的初速为2v₀，向左，加速度向右，大小为(a₂+a₁)，减速至零，A对B的位移为L，则由v_t²－v₀²＝2as得(2v₀)²＝2(a₁+a₂)L，即

2、加速度：描述速度变化的快慢和方向的物理量，是速度的变化和所用时间的比值：a＝ΔV/Δt，单位：m／s²．加速度是矢量，它的方向与速度变化(ΔV)的方向相同．

1、速度的变化：△V=V_t－V₀，描述速度变化的大小和方向，是矢量

3．位移公式：S＝vt．

2．特点：a＝0，v=恒量．