做功可以改变物体的能量．所有外力对物体做的总功等于物体动能的增量． W₁+W₂+W₃+……＝½mv_t²－½mv₀²

1．反映了物体动能的变化与引起变化的原因--力对物体所做功之间的因果关系．可以理解为外力对物体做功等于物体动能增加，物体克服外力做功等于物体动能的减小．所以正功是加号，负功是减号。

4、实际问题中的功率

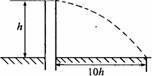[例8]推动节水工程的转动喷水“龙头”。如图所示，龙头距地面h，其喷灌半径可达10h，每分钟喷水质量为m，所用水从地面下H的井中抽取，设水以相同的速率喷出，水泵的效率为η，水泵的功率P至少多大？

解析:水泵对水做功，用来增大水的重力势能和动能．

设水喷出时速度为v，则h=½gt²,10h=vt;解得

每分钟内水泵对水做的功W＝mg(H+h)+½mv²=mg(H+26h)，又W=ηPt,∴

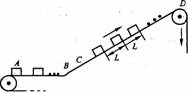[例9]一传送带装置示意如图，其中传送带经过AB区域时是水平的，经过BC区域时变为圆弧形(圆弧由光滑模板形成，未画出)，经过CD区域时是倾斜的，AB和CD都与BC相切。现将大量的质量均为m的小箱一个一个在A处放到传送带上，放置时初速为零，经传送带运送到D处，D和A的高度差为h。稳定工作时传送带速度不变，CD段上各箱等距排列，相邻两箱的距离为L。每个箱子在A处投上后，在到达B之前已经相对于传送带静止，且以后也不再滑动(忽略经BC段时的微小滑动)。己知在一段相当长的时间T内，共运送小货箱的数目为N，这装置由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦。求电动机的平均输出功率P。

[解析]以地面为参考(下同)，设传送带的运动速度为v₀，在水平段运输的过程中，小货箱先在滑动摩擦力作用下做匀加速运动，设这段路程为S，所用时间为t，加速度为a，则对小箱有：S＝½at²……①

　 v₀＝at………②。在这段时间内，传送带运动的路程为：S₀= v₀t……③，由以上可得S₀＝2S……④。用f表示小箱与传送带之间的滑动摩擦力，则传送带对小箱做功为：W₁=fS=½mv₀²……⑤；传送带克服小箱对它的摩擦力做功：W₀=Fs₀=2·½mv₀²……⑥

两者之差就是克服摩擦力做功发出的热量：Q=½mv₀²……⑦

可见，在小箱加速运动过程中，小箱获得的动能与发热量相等。

T时间内，电动机输出的功为：W=PT……⑧

此功用于增加小箱的动能、势能以及克服摩擦力发热,即W=½Nmv₀²十Nmgh+NQ……⑨

已知相邻两小箱的距离为L，所以：v₀T＝NL……⑩

联立⑦⑧⑨⑩得。

散　　　　　 　动能　 动能定理

知识简析一、动能

　　 如果一个物体能对外做功，我们就说这个物体具有能量．物体由于运动而具有的能．　 E_k＝½mv²，其大小与参照系的选取有关．动能是描述物体运动状态的物理量．是相对量。

3、汽车起动问题分析

(1)当以恒定功率运动时，做加速度越来越小的变加速直线运动，a=－，当F_牵＝f时，加速度a＝0，此时的速度为最大速度．所以v_m=p/f，以后机车做匀速直线运动。

(2)欲使汽车从静止开始做匀加速直线运动，一开始不能用额定功率，功率必须随着速度增加而增加，使P/v=F恒定；这种运动持续一段时间后．汽车又做加速度越来越小的加速运动，最后达到最大速度v_m，所以求匀加速直线运动的时间不可用t=v_m/a，必须用v=P_额/F　 ，而t=v/a，　　 由此得：t= P_额/Fa

[例7]质量为lkg的机械与平面间摩擦力f=2N，其额定功率为12 W，要使它以a＝lm／s²的加速度做匀加速直线运动，问做这种运动的最长时间为多少？

　　 错解：v_m＝P/f＝6m／s，　　　　 t=v_m/a=6s

　 解析：以上做法错在何处，我们进行如下的分析：要使a＝lm／s²，必须F＝f+ma＝3N

要使F=3N速度最大为v=P/F=4m／s　　 所以做匀加速直线运动的时间为t=v/a=4s

这里可做这样的检验：当速度大于4m／s 时，不妨设为5 m／s ；F=P/v=2．4N，则加速度a=(F－f)/m=0．4 m／s²，显然不是匀加速直线运动了，所以一旦速度大于4m／s 时，由于功率不再增加，加速度则变小，做的是加速度越来越小的加速直线运动，直到加速度为零，之后做匀速运动．答案：4 s

点评(1)此类问题关键是发动机的功率是否达到额定功率，若在额定功率下起动，则一定是交加速运动，因为牵引力随速度的增大而减小．求解时不能用匀变速运动的规律来解．具体变化过程可用如下示意图表示．

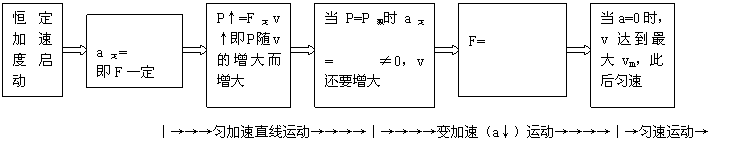　　 (2)特别注意匀加速起动时，牵引力恒定．当功率随速度增至预定功率时的速度(匀加速结束时的速度)，并不是车行的最大速度．此后，车仍要在额定功率下做加速度减小的加速运动．(这阶段类同于额定功率起动)直至a=0时速度达到最大．具体变化过程可用如下示意图

[例]一辆汽车在平直的公路上以速度v₀开始加速行驶，经过一段时间t，前进了距离s，此时恰好达到其最大速度V_m.设此过程中汽车发动机始终以额定功率P工作，汽车所受的阻力恒定为F，则在这段时间里，发动机所做的功为(　　 )

A、 Fv_mt；B、Pt；C、½mv_m²+Fs－½mv₀²；D、；

解析：汽车在恒定功率作用做变牵引力的加速运动，所以发动机做功为变力做功，根据P=W/t可求得W=Pt，而P=F^/v=Fv_m，所以W= Fv_m t；根据能量守恒：W+½mv₀²=½mv_m²+Fs

所以W=½mv_m²+Fs－½mv₀²；答案：ABC

思考：为何用得到不正确？错在哪里？

[例]质量为m = 4000kg的卡车，额定输出功率为P=60 kW。当它从静止出发沿坡路前进时，每行驶100 m，升高5m，所受阻力大小为车重的0.1倍，取g=10 m/s² .

试求：(1)卡车能否保持牵引力为8000 N不变在坡路上行驶？

(2)卡车在坡路上行驶时能达到的最大速度为多大？这时牵引力为多大？

(3)如果卡车用4000 N牵引力以12m/s的初速度上坡，到达坡顶时，速度为4 m/s,那么卡车在这一段路程中的最大功率为多少？平均功率是多少？

分析:汽车能否保持牵引力为8000 N上坡要考虑两点：第一，牵引力是否大于阻力？第二，汽车若一直加速，其功率是否将超过额定功率，依P=Fv解。本题考查了汽车牵引力恒定时功率的计算。不少同学在得到F > f + mgsinθ后，立即做出结论：汽车可以保持牵引力8000 N不变上坡；而没有考虑到汽车由于加速，速度不断增大，其功率不断增大，如果坡路足够长，这种运动方式是不允许的。

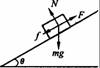解：分析汽车上坡过程中受力情况如图所示：牵引力F,重力mg＝4×10⁴N，f＝kmg＝4×10³ N，支持力N，依题意sinθ＝5/100。

(1)汽车上坡时，若F＝8000N,而f+mgsinθ＝4×10³+4×10⁴×1/20＝6×10³ N,即F> f +mgsinθ,汽车将加速上坡，速度不断增大，其输出功率P=Fv也不断增大，长时间后，将超出其额定输出功率，所以，汽车不能保持牵引力为8000N不变上坡。

　(2)汽车上坡时，速度越来越大，必须不断减小牵引力以保证输出功率不超过额定输出功率，当牵引力F= f + mgsinθ=6×10³ N时，汽车加速度为零，速度增大到最大，设为v_m，则P＝Fv＝(f+mgsinθ)·v_m；

F= f + mgsinθ=6×10³ N

(3)若牵引力F=4000N，汽车上坡时，速度不断减小，所以最初的功率即为最大，P=Fv=4000×12=48×10³w。整个过程中平均功率为=32×10³W

规律方法　 1、功率的计算方法

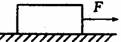[例1]如图所示，质量为lkg的物体与平面间摩擦系数μ=0．l(g取10m／s²)，在2 N水平拉力作用下由静止开始运动了2s，求这段时间内拉力、摩擦力、重力、支持力的平均功率及2s末的即时功率各为多少？

　 解析：a==1m／s²．s＝½at²＝2m．　　 v＝at＝2m/s

　　 外力 F做功功率．平均值为：p₁＝W/t=Fs/t=2W　　 2s末即时功率为：P₁^/=Fv＝4 W

　　 摩擦力做功功率．平均值：P₂=fs/t=1W　　 2 s末即时功率为：P₂^/=fv= 2 W

　　 重力与支持力N由P=Fvcosθ知：功率都为0．

答案：外力F平均功率和即时功率分别为2W、4W；摩擦力平均功率和即时功率分别为1W、2W；重力和支持力功率都为0．

　　 点评：(1)明确是什么力做功功率；　　 (2)清楚是平均功率还是即时功率．

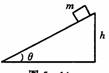[例2]如图所示，质量为m的物体沿高为h的光滑斜面滑下到达底端时重力的即时功率为多少？

错解：由机械能守恒定律可知到达底端速度v=，所以此时功率P＝mgv=mg：提示：这里没有注意到mg与v的夹角，应当为P= mgsinθ

点评：做题时注意力跟速度的夹角．

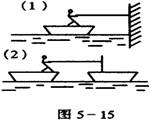
[例3]一个小孩站在船头，按应当为图5-15两种情况用同样大小力拉绳，经过相同的时间t(船未碰撞)，小孩所做的功W₁、W₂及在时间t内小孩拉绳的功率 P₁、P₂的关系为(　 )

A．W₁＞W₂，P₁= P₂　　 B．W₁＝W₂，P₁＝P₂　　

C．W₁＜W₂，P₁＜P₂　　 D．W₁＜W₂，P₁= P₂

　　 提示：两种情况中拉力对人做的功一样，第二种情况拉力除对人做功外，又对另一只小船也做了功，所以W₂＞W₁．由于所用时间一样，所以P₂＞P₁．　　 答案：C

　　 点评：应弄清哪一个力对哪一个物体做功，其功率是什么

2、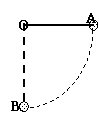两种功率

[例4]长为L的细线一端固定在O点，另一端系一质量为m的小球，开始时，细线被拉直，并处于水平位置，球处在0点等高的A位置，如图所示，现将球由静止释放，它由A运动到最低点B的过程中，重力的瞬时功率变化的情况是　　　　　　　　　　　　　　　　 ( )

A.一直在增大　　 B.一直在减小　　 C.先增大后减小　　 D.先减小后增大

解析:小球在A位置时速度为零，重力的瞬时功率为零，到达B位置时，速度达到最大，方向水平向左，与重力夹角为90⁰，P_B＝0，由于两个极端位置瞬时功率均为0，故可判断C正确．

点评:物体在恒力作用下的变速运动或在变力作用下的运动，力做功的瞬时功率一般都随时间变化，因此，在求某力在某时的瞬时功率或讨论某力做功的瞬时功率随时间的变化时，都应根据公式P=Ftcosα来进行分析和计算．

　　 [例5](1994年上海高考题)跳绳是一种健身运动。设某运动员的质量是50kg，他一分钟跳绳180次。假定在每次跳跃中，脚与地面的接触时间占跳跃一次所需时间的2/5，则该运动员跳绳时克服重力做功的平均功率是＿。(g取10m/s²)

　解析：把运动员每次跳跃转换成质点做竖直上抛运动模型。每次跳跃总时间

T＝60/180＝1/3s．　 　每次腾空的时间t=(l一)=0．02s。

每次腾空高度　 h=½g(t/2)²=½×10×(0．02/2)²＝0．05m。

每次腾空上升时克服重力做的功　 W=mgh=50×10×0．05＝25J。

　　 把每次跳跃总时间T内的触地过程、下落过程舍弃，简化成在T内就是单一竖直上升克服重力做功的过程，故可解出 P＝W/T＝25／(1/3)=75 W。

点评：综上所述不难发现，灵活地转换物理模型是一种重要的物理思想方法。学会这种方法，就会使我们在解决物理问题时变得从容自如，巧解速解物理问题，从而提高学习的效率。

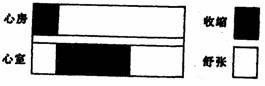[例6]随着生活水平的提高，伴随着心血管病也比以前增加了．为了提高生活质量，延长人的寿命，掌握心血管健康活动的常识就显得十分重要，心脏在人的一生之中之所以能够　 不停地跳动而不疲倦，其原因之一在于它的活　 动具有节律性，图中是心脏每跳动一次，心房和心室的舒张、收缩情况：

　(1)从图分析，心脏在人的一生中不停地跳动，为什么不会疲倦？

　(2)如果有人心率为75次／min，则每搏的输出量为70ml，每分钟输出量为　　　　 ，一般情况下，长跑运动员与正常人相比，心率较慢，但　　　　　 较多，所以能满足运动时的供血．

　(3)如果有人的心率为 75次／min，则心脏每跳动一次所需的时间是　　　　 ，心房、心室共同处于　　　　　　 期，所占的时间约为　　　　　　　　

　 (4)若某人的心脏每分钟跳动75次，心脏收缩压为135mmHg(lmmHg＝133．322Pa)收缩一次输出血量平均为70ml，那么心脏收缩时的平均功率有多大？

　解析：(1)从图中可以看出，如果心率是75次／min，其中心房只工作(收缩)了0．1s，休息(舒张)了0．7s，心室工作了0．3s，休息了0．5s，可见心脏每跳动一次，心房、心室的舒张期比收缩期长，心脏有充分休息的时间，因此人的一生，心脏不停地跳动而不知疲倦．

　　 (2)5250ml(每搏输出量是指心脏跳动一次，心脏收缩时向动脉输出的血量，每收缩一次输出70ml，每分输出量为70×75=5250ml)

　　 经常参加体育锻炼的人，心肌发达，搏动有力，每搏输出量比一般人要大．

　　 (3)0．8s　 舒张0．4s(心脏每分钟跳动的次数叫心率)

　　 (4)心脏收缩一次做功：W=P·ΔV

　　 ∵P=135mmHg＝1．8×10⁴Pa　　　 ΔV＝70ml＝7×10^－5m3

　　 ∴W＝1．8×10⁴Pa×7×10^－5m3＝1．26J ∴每分钟，心脏做功W^/=75×1．26=94．5J

　　 ∴心脏收缩时平均功率为=94．5/60=1．6W

4．我们处理问题时必须清楚是哪一个力的功率，如一个机械的功率为P，这里指的是牵引力的功率，不可认为是机械所受合外力的功率．

3．P＝Fv应用时，F、v必须同向，否则应分解F或v，使二者同向．这里的P=Fv实际上是Fvcosθ、θ为F、v夹角．

2．P＝Fv当v为平均值时为平均功率，当v为即时值时为即时功率．

1．P＝W／t 所求的是这段时间内平均功率．

4、做功求解的典型情况

①注意力、冲量、功的区别

　　 除了它们的物理定义、单位以及是标量还是矢量以外，从动力学观点来看：(1)力和物体的运动状态的变化存在着瞬时因果关系，即力是产生加速度的原因，有力才有加速度，力变加速度变，它们之间的因果规律用牛顿第二定律来表达．(2)力的冲量反映的是力持续在一段时间的作用效果的累积量．其结果是要引起物体动量的改变，它们之间的因果规律用动量定理来表达．(3)功是力持续作用在一段空间位移上的作用效果的累积量，是标量．其结果是要引起物体动能的改变，它们之间的因果规律用动能定理来表达．

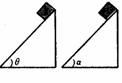[例4]如图所示，质量相等的两物体沿相同高度不同倾角的两光滑斜面由静止滑下，到达底端的过程中，两情况(　　　 )

　　 A．重力冲量相等

　　 B．重力做功相等

　　 C．物体受合外力冲量相等

　　 D．物体受合外力做功相等

　　 解析： A．重力冲量大小不相等，由于所用时间不同，因而不相等；B．重力做功相等，重力做功特点是只与始末位置而跟路径无关；C．物体所受合外力冲量大小相等，都为m，由于∠θ≠∠α，所以方向不同；D．物体所受合外力做功相等，都为mgh．答案：BD

②作用力和反作用力的做功

作用力与反作用力同时存在，作用力做功时，反作用力可能做功，也可能不做功，可能做正功，也可能做负功，不要以为作用力与反作用力大小相等、方向相反，就一定有作用力、反作用力的功数值相等，一正一负．所以作用力与反作用力做功不一定相等，但冲量的大小相等．

[例5]以下说法正确的是(　　　 )

　A．摩擦力可以对物体做正功　　 B．摩擦力可以使物体的速度发生变化，但对物体不做功

　C．作用力与反作用力做功一定相等　　 D．一对平衡力做功之和为零

解析：A．摩擦力可以对物体做正功，只要摩擦力的方向与物体运动方向相同，摩擦力就做正功．摩擦力可以改变物体的速度，对物体有一个冲量作用，但物体在力的方向上没有位移，因而不做功，如随圆板一起转动的物体．由此可以认识到：力对物体有冲量，但不一定对物体做功，相反只要力对物体做功，一定会有冲量．又可进一步认识：力使物体动量发生变化，其动能不一定变化；但力使物体动能发生变化时，其动量一定发生变化．c．作用力与反作用力做功不一定相等，如一炸弹炸成质量为m与 2 m的两块，根据动量守恒mv₁=2mv₂， 则v₁=2v₂，作用力和反作用力做功为W₁=½m(2v₂)²与W₂=½mv₂²，所以不相等。可认识到：作用力和反作用力产生的冲量总是大小相等，但做功可能不相等．D．一对平衡力合力为零，所以二力合力做功为零．答案：ABD

③摩擦力的做功

　A、静摩擦力做功的特点

(1)静摩擦力可以做正功，也可以做负功，还可以不做功。

(2)在静摩擦力做功的过程中，只有机械能的相互转移(静摩擦力起着传递机械能的作用)，而没有机械能转化为其他形式的能．

(3)相互摩擦的系统内，一对静摩擦力所做功的代数和总为零。

　B．滑动摩擦力做功的特点

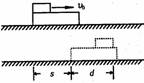
如图所示，上面不光滑的长木板，放在光滑的水平地面上，一小木块以速度V₀从木板的左端滑上木板，当木块和木板相对静止时，木板相对地面滑动了S，小木块相对木板滑动了d，则由动能定理知：

滑动摩擦力对木块所做功为：　 W_木块=一f(d+S)……①

滑动摩擦力对木板所做功为：　 W_木板=fs……②

所以，木块动能增量为：　 ΔE_K木块=一f(d+s)……③

木板动能增量为：　 ΔE_K木板=fs………④

由③④得：ΔE_K木块+ΔE_K木板=一fd………⑤

⑤式表明木块和木板组成的系统的机械能的减少量等于滑动摩擦力与木块相对木板的位移的乘积。这部分减少的能量转化为内能。

故滑动摩擦力做功有以下特点：

1)滑动摩擦力可以对物体做正功，也可以对物体做负功，当然也可以不做功。

2)一对滑动摩擦力做功的过程中，能量的转化有两个方面：一是相互摩擦的物体之间机械能的转移；二是机械能转化为内能。转化为内能的量值等于滑动摩擦力与相对位移的乘积。

3)滑动摩擦力、空气摩擦阻力等，在曲线运动或往返运动时等于力和路程(不是位移)的乘积

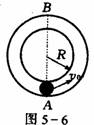[例6]如图所示，半径为R的孔径均匀的圆形弯管水平放置，小球在管内以足够大的初速度v₀在水平面内做圆周运动，小球与管壁间的动摩擦因数为μ，设从开始运动的一周内小球从A到B和从B到A的过程中摩擦力对小球做功分别为W₁和W₂，在这一周内摩擦力做的总功为W₃，则下列关系式正确的是(　　 )

　 A．W₁＞W₂ 　B．W₁＝W₂　 C． W₃＝ 0　 D． W3＝W₁+W₂

解析：求某一力对物体所做的功值有多种思路，对于恒力(大小、方向均不变的力)做功的情况，通常由w＝Fscosα求解．对于变力(特别是方向发生变化的力)做功的情况，一般由功能转换关系求解．对于后一种思路，一定要正确判断哪些力做功，在外力做功的过程中，物体(或系统)的能量如何发生变化，变化了多少．

　 小球在水平弯管内运动，滑动摩擦力始终与速度方向相反，做负功，而小球在水平面内的圆周运动的向心力是由外管壁对小球的弹力N提供的，由于转动半径R始终不变，摩擦力对小球做负功，小球运动的速率逐渐减小，向心力减小即N减小，而f＝μN，滑动摩擦力f也减小，即由下列关系：

　　 N=Fn=mv²/R　　 m，R不变，v减小，则N减小，

　　 f＝μN　 N减小，则f减小

　　 W=－fπR　　 f减小，则W减小

　　 所以W₁＞W₂

　　 W₁．W₂都为负功，因此W₃＝W₁+W₂．答案：AD

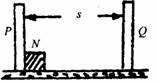[例7]如图所示，PQ是固定在水平桌面上的固定挡板，质量为m的小木块N从靠近P以一定的初速度向Q运动，已知物块与桌面间的动摩擦因数为μ，P与Q相距为s，物块与Q板碰撞n次后，最后静止于 PQ的中点，则整个过程摩擦力所做的功为多少？(n为自然数)

　　 解析：物块与Q板碰撞n次后，最后停在PQ中点，会有两种可能，一种可能是与Q板碰后向P板运动至中点而停止，设与Q板碰撞n次，则物体运动的路程为(2n一)s，摩擦力所做的功为W_f1=μmg(2n一)s

　　 第二种可能是物块与Q板碰后再与P板碰撞向Q板运动至中点而停止，在这种情况下，物体运动的路程为(2n+)s ，摩擦力所做的功为 W_f2= μmg(2n+)s，两种情况下，摩擦力对物体均做负功。

　　 扩展与研究：两类不同的力，一类是与势能相关的力，如重力、弹簧的弹力、电场力等，它们的功与路程无关系，只与位移有关。另一类是滑动摩擦力，空气阻力等，这类力做功与物体的运动路径有关。在上例中，滑动摩擦力是一个变力，方向在变化，可转化为恒力做功，同时滑动摩擦力做功要看物体运动的路程，这是摩擦力做功的特点，必须牢记。

点评：求功的思路共有四条:(1)由功的定义．恒力做功；(2)由能量关系求解；(3)由功率的定义；(4)由动能定理求解．

试题展示

功率

3、变力做功问题

①W＝F·scosα是用来计算恒力的功，若是变力，求变力的功只有通过将变力转化为恒力，再用W＝Fscosα计算．

②有两类不同的力：一类是与势能相关联的力，比如重力、弹簧的弹力以及电场力等，它们的功与路径无关，只与位移有关或者说只与始末点的位置有关；另一类是滑动摩擦力、空气阻力等，在曲线运动或往返运动时，这类力(大小不变)的功等于力和路程(不是位移)的积．

③根据功和能关系求变力的功．如根据势能的变化求对应的力做的功，根据动能定理求变力做的功，等等．

④根据功率恒定，求变力的功，W=Pt.

⑤求出变力F对位移的平均力来计算，当变力F是位移s的线性函数时，平均力．

⑥作出变力F随位移，变化的图象，图象与位移轴所围均“面积”即为变力做的功．

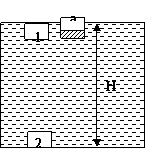[例]面积很大的水池，水深为H，水面上浮着一正方体木块，木块边长为a。，密度为水密度的½，质量为m,开始时，木块静止，如图所示，现用力F将木块缓慢地压到水池底，不计摩擦，求：

　(1)从木块刚好完全没人水中到停止在池底的过程中，池水势能的改变量．

　(2)从开始到木块刚好完全没入水中的过程中，力F所做的功．

解析:(1)木块刚好没入水中到到达池底的过程中,相当于有相同体积的水从池底到达水面,因木块的密度为水的冗长度的½,故相同体积的水的质量为2m,,故池水势能的改变量为ΔE_P=2mg(H－a);

(2)因水池面积很大,可忽略因木块压入而引起的水深的变化,木块刚好完全没入水中时,图中原来划线区域的水被排开,相当于这部分水平铺于水面,这部分水的质量为m,其势能的改变量为:

木块势能的改变量为:

根据动能定理,力F做的功为:W=ΔE_水+ΔE_木=¼mga.

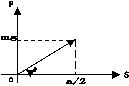
　(2)又解：从开始到木块完全没入水中的过程，力F所做的功为变力功．也可画出Fs图象，做功在数值上等于Fs图线与位移S轴所围图形的面积的数值，在压下木块过程中，力F与位移s成正比，从开始到完全没入水中，力F的位移为½a，作出F-s图象如图,,据图象可求得做功W=½×½amg=¼mga..