
3、 电场力做功与能量的变化应用
电场力做功,可与牛顿第二定律,功和能等相综合,解题的思路和步骤与力学中的完全相同,但要注意电场力做功的特点--与路径无关
 [例10]如图所示,有两个完全相同的金属球A、B,B固定在绝缘地板上,A在离B高H的正上方由静止释放,与B发生正碰后回跳高度为h,设碰撞中无动能损失,空气阴力不计,
[例10]如图所示,有两个完全相同的金属球A、B,B固定在绝缘地板上,A在离B高H的正上方由静止释放,与B发生正碰后回跳高度为h,设碰撞中无动能损失,空气阴力不计,
A、若A、B带等量同种电荷,则h>H B、若A、B带等量异种电荷,则h<H
C、若A、B带等量异种电荷,则h>H D、若A、B带等量异种电荷,则h=H
解析:若A、B带等量同种电荷,则碰撞后两球带电量不变,下落过程中重力做正功,电场力做负功,回跳时重力做负功,电场力做正功。由能量守恒定律得h=H;若A、B带等量异种电荷,则碰撞过程中重力做正功,电场力做正功,回跳过程中需克服重力做功。故h>H,答案C
 [例11] 已知如图,光滑绝缘水平面上有两只完全相同的金属球A、B,带电量分别为-2Q与-Q。现在使它们以相同的初动能E0(对应的动量大小为p0)开始相向运动且刚好能发生接触。接触后两小球又各自反向运动。当它们刚好回到各自的出发点时的动能分别为E1和E2,动量大小分别为p1和p2。有下列说法:①E1=E2> E0,p1=p2> p0 ②E1=E2= E0,p1=p2= p0 ③接触点一定在两球初位置连线的中点右侧某点 ④两球必将同时返回各自的出发点。其中正确的是
[例11] 已知如图,光滑绝缘水平面上有两只完全相同的金属球A、B,带电量分别为-2Q与-Q。现在使它们以相同的初动能E0(对应的动量大小为p0)开始相向运动且刚好能发生接触。接触后两小球又各自反向运动。当它们刚好回到各自的出发点时的动能分别为E1和E2,动量大小分别为p1和p2。有下列说法:①E1=E2> E0,p1=p2> p0 ②E1=E2= E0,p1=p2= p0 ③接触点一定在两球初位置连线的中点右侧某点 ④两球必将同时返回各自的出发点。其中正确的是
A.②④ B.②③ C.①④ D.③④
解析:由牛顿定律的观点看,两球的加速度大小始终相同,相同时间内的位移大小一定相同,必然在连线中点相遇,又同时返回出发点。由动量观点看,系统动量守恒,两球的速度始终等值反向,也可得出结论:两球必将同时返回各自的出发点。且两球末动量大小和末动能一定相等。从能量观点看,两球接触后的电荷量都变为-1.5Q,在相同距离上的库仑斥力增大,返回过程中电场力做的正功大于接近过程中克服电场力做的功,由机械能定理,系统机械能必然增大,即末动能增大。选C。
拓展:两个相同的带电小球(可视为点电荷),相碰后放回原处,相互间的库仑力大小怎样变化?讨论如下:①等量同种电荷,F /=F;②等量异种电荷,F /=0<F;③不等量同种电荷F />F;④不等量异种电荷F />F、F
/=F、F
/<F都有可能,当满足q1=(3±2 )q2时F /=F。
)q2时F /=F。
[例12]为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是面积A=0.04 m2的金属板,间距L=0.05 m,当连接到U=2500V的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示.现把一定量均匀分布的烟尘颗粒密闭在容器内,每m3有烟尘颗粒1013个.假设这些颗粒都处于静止状态,每个颗粒带电量为q=1.0×10-17C,质量为m= 2.0×10-15kg,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力.求合上开关后:(1)经过多长时间烟尘颗粒可以
 被全部吸附?(2)除尘过程中电场对烟尘颗粒共做了多少功?(3)经过多长时间容器中烟尘颗半粒的总动能达到最大?
被全部吸附?(2)除尘过程中电场对烟尘颗粒共做了多少功?(3)经过多长时间容器中烟尘颗半粒的总动能达到最大?
解析:(1)由题可知,只要距离上板表面的烟尘能被吸附列下板时,烟尘即被认为全却吸收,烟尘所受电场力为F=qU/L,L=½at2= ,得
,得 .
.
(2)由于板间烟尘颗粒均匀分布,可以认为烟尘的质心位于板间中点位置,因此,除尘过程中电场力对烟尘所做的总功为W=½NALqU=2.5×10-4J
(3)解法一:设烟尘颗粒下落距离为x,则板内烟尘总动能EK=½mv2·NA (L-x)= ,当x=L/2时,EK达到最大.又据x=½at12,则
,当x=L/2时,EK达到最大.又据x=½at12,则
解法二:假定所有烟尘集中于板中央,当烟尘运动到下板时,系统总动能录大,则L/2=½at12,所以
[例13]在电场强度为E的匀强电场中,有一条与电场线平行的几何线,如图中虚线所示。几何线上有两个静止的小球A和B(均可视为质点),两小球的质量均为m,A球带电荷量+Q,B球不带电。开始时两球相距L,在电场力的作用下,A球开始沿直线运动,并与B球发生正对碰撞,碰撞中A、B两球的总动能无损失。设在各次碰撞过程中,A、B两球间无电量转移,且不考虑重力及两球间的万有引力,问:
 (1)A球经过多长时间与B球发生第一次碰撞?
(1)A球经过多长时间与B球发生第一次碰撞?
(2)第一次碰撞后,A、B两球的速度各为多大?
(3)试问在以后A、B两球再次不断地碰撞的时间间隔会相等吗?如果相等,请计算该时间间隔T。如果不相等,请说明理由。
解答:(1)A球在电场力作用下做匀加速直线运动  ①
①
 ② 联立①②两式得
② 联立①②两式得  ③
③
(2)A球与B球碰撞,动量守恒  ④
④
据题意,总动能不损失  ⑤
⑤
联立④⑤两式得
 ⑥
⑥  ⑦
⑦
(3)以B球为参考系,A、B碰撞后,A球以vA向左做匀减速直线运动,经时间t后,速度减为0,同时与B球相距为L,然后A球又向右做匀加速直线运动,又经时间t后,速度增为vA,与B球发生第二次碰撞。同(2)理可证,每次总动能无损失的碰撞均是交换速度,则以后第三、四次碰撞情况可看成与第一、二次碰撞情况重复,以此类推可知A、B两球不断碰撞的时间间隔相等,均为T=2t= ⑧
⑧
 [例14]有三根长度皆为l=1.00 m的不可伸长的绝缘轻线,其中两根的一端固定在天花板上的O点,另一端分别拴有质量皆为m=1.00×10-2 kg的带电小球A和B,它们的电量分别为-q和+q,q=1.00×10-7 C.A、B之间用第三根线连接起来.空间中存在大小为E=1.00×106
N/C的匀强电场,场强方向沿水平向右,平衡时A、B球的位置如图所示. 现将O、B之间的线烧断,由于有空气阻力,A、B球最后会达到新的平衡位置.求最后两球的机械能与电势能的总和与烧断前相比改变了多少.(不计两带电小球间相互作用的静电力)
[例14]有三根长度皆为l=1.00 m的不可伸长的绝缘轻线,其中两根的一端固定在天花板上的O点,另一端分别拴有质量皆为m=1.00×10-2 kg的带电小球A和B,它们的电量分别为-q和+q,q=1.00×10-7 C.A、B之间用第三根线连接起来.空间中存在大小为E=1.00×106
N/C的匀强电场,场强方向沿水平向右,平衡时A、B球的位置如图所示. 现将O、B之间的线烧断,由于有空气阻力,A、B球最后会达到新的平衡位置.求最后两球的机械能与电势能的总和与烧断前相比改变了多少.(不计两带电小球间相互作用的静电力)
[解析] 图1中虚线表示A、B球原来的平衡位置,实线表示烧断后重新达到平衡的位置,其中α、β分别表示细线OA、AB与竖直方向的夹角.
 A球受力如图2所示:重力mg,竖直向下;电场力qE,水平向左;细线OA对A的拉力T1,方向如图;细线AB对A的拉力T2,方向如图.由平衡条件
A球受力如图2所示:重力mg,竖直向下;电场力qE,水平向左;细线OA对A的拉力T1,方向如图;细线AB对A的拉力T2,方向如图.由平衡条件
T1sinα+T2sinβ=qE, T1cosα=mg+T2cosβ
B球受力如图3所示:重力mg,竖直向下;电场力qE,水平向右;细线AB对B的拉力T2,方向如图.由平衡条件
T2sinβ=qE, T2cosβ=mg
 联立以上各式并代入数据,得α=0, β=45°
联立以上各式并代入数据,得α=0, β=45°
 由此可知,A、B球重新达到平衡的位置如图4所示.与原来位置相比,A球的重力势能减少了EA=mgl(1-sin60°)
由此可知,A、B球重新达到平衡的位置如图4所示.与原来位置相比,A球的重力势能减少了EA=mgl(1-sin60°)
B球的重力势能减少了EB=mgl(1-sin60°+cos45°)
A球的电势能增加了WA=qElcos60°
B球的电势能减少了WB=qEl(sin45°-sin30°)
两种势能总和减少了W=WB-WA+EA+EB
代入数据解得W=6.8×10-2 J
 电场中的导体、电容器
电场中的导体、电容器
知识简析 一、电场中的导体
2、 公式E=U/d的理解与应用
(1)公式E=U/d反映了电场强度与电势差之间的关系,由公式可知,电场强度的方向就是电势降低最快的方向.
(2)公式E=U/d只适用于匀强电场,且d表示沿电场线方向两点间的距离,或两点所在等势面的范离.
(3)对非匀强电场,此公式也可用来定性分析,但非匀强电场中,各相邻等势面的电势差为一定值时,那么E越大处,d越小,即等势面越密.

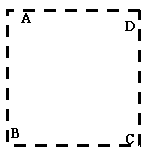 [例7]如图所示,A、B、C、D是匀强电场中一正方形的四个顶点,已知A、B、C三点的电势分别为φA=15 V, φB=3 V, φC=-3 V,由此可得D点电势φD=
。
[例7]如图所示,A、B、C、D是匀强电场中一正方形的四个顶点,已知A、B、C三点的电势分别为φA=15 V, φB=3 V, φC=-3 V,由此可得D点电势φD=
。
解法一、假设在此电场中移动一正电荷q,从A点移到B点,设AB与电场方向夹角为θ,则WAB=qE·ABcosθ=qE·DCcosθ=WDC即从A点移到B点与从D点移到C点电场力做功相同,所以有WAB=qUAB=qUDC=q(φD-φC),即φD=UAB+φC=15-3-3=9V
解法二.设此正方形对角线的交点为O,则由U=Ed可知φA-φO=UAO=UOC=φO-φC,UBO=UOD=φB-φO=φO-φD,即 ,上式代入数据得φD=9 V
,上式代入数据得φD=9 V
解法三:如图所示,连接AC,在AC上取E、F两点,使AE=EF=FC,则 UAC=UAE+UEF+UFC,UAE=UEF=UFC=UAC/3,解得φF=3 V, φE=9V
连接BF和DE,因φB=φF=3 V,所以BF是等势面,又因为BF// DE,所以DE也是等势面,即φD=9V。
 思考:作出该电场的电场线分布图.
思考:作出该电场的电场线分布图.
[例8]某静电场沿x方向的电势分布如图所示,则()
A、在0-xl之间不存在沿x方向的电场
B、在0-xl之间存在着沿x方向的匀强电场
C、在x1-x2之间存在着沿x方向的匀强电场
D、在x1-x2之间存在着沿x方向的非匀强电场
解析:在0-xl之间电势不变,即在0-xl之间等势,故在此方向无电场;在x1-x2之间电势随距离均匀减小,则在x1-x2之间有沿x轴正方向的匀强电场,故A、C正确。答案:AC
 [例9] 如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是: [ ]
[例9] 如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是: [ ]
A.电荷从a到b加速度减小; B.b处电势能大
C.b处电势高; D.电荷在b处速度小
解析:由图可知b处的电场线比a处的电场线密,说明b处的场强大于a处的场强。根据牛顿第二定律,检验电荷在b处的加速度大于在a处的加速度,A选项错。
由图可知,电荷做曲线运动,必受到不等于零的合外力,即Fe≠0,且Fe的方向应指向运动轨迹的凹向。因为检验电荷带负电,所以电场线指向是从疏到密。再利用“电场线方向为电势降低最快的方向”判断a,b处电势高低关系是UA>UB,C选项不正确。
根据检验电荷的位移与所受电场力的夹角大于90°,可知电场力对检验电荷做负功。功是能量变化的量度,可判断由a→b电势能增加,B选项正确;又因电场力做功与路径无关,系统的能量守恒,电势能增加则动能减小,即速度减小,D选项正确。
2.特点
(1)各点电势相等.
(2)等势面上任意两点间的电势差为零.
(3)电荷沿着等势面运动,电场力不做功.
(4)处于静电平衡状态的导体是一个等势体,其面为等势面.
(5)匀强电场,电势差相等的等势面间距离相等,点电荷形成的电场,电势差相等的等势面间距不相等,越向外距离越大.
(6)等势面上各点的电势相等但电场强度不一定相等.
(7)电场线跟等势面垂直,且由电势高的面指向电势低的面
(8)两个等势面永不相交.
 [例3]如图所示,匀强电场中的一组等势面,A、B、C、D相邻间距离为2cm,则场强 E=
;离A点1.5cm的P点电势为
V.
[例3]如图所示,匀强电场中的一组等势面,A、B、C、D相邻间距离为2cm,则场强 E=
;离A点1.5cm的P点电势为
V.
解析:E=U/SABsin600=1000 /3V/m
/3V/m
UBp=E·SBPsin600=1000 /3×0.5×10-2×
/3×0.5×10-2× /2V=2.5V
/2V=2.5V
BP之间电势差为2.5V,由于UP<UB, 所以 Up=-2.5 V
点评:在我们应用U=Ed公式时一定要注意d是沿着电场线方向的距离,或者说是两等势面间的距离.
 [例4]如图所示,实线为匀强电场中的电场线,虚线为等势面,且相邻等势面间的电势差相等。一正点电荷在等势面A处的动能为20J,运动到等势面C处的动能为零。现取B等势面为零电势能面,则当此电荷的电势能为20J时的动能是
J。(不计重力和空气阻力)
[例4]如图所示,实线为匀强电场中的电场线,虚线为等势面,且相邻等势面间的电势差相等。一正点电荷在等势面A处的动能为20J,运动到等势面C处的动能为零。现取B等势面为零电势能面,则当此电荷的电势能为20J时的动能是
J。(不计重力和空气阻力)
解析:设相邻等势面间的电势差为△U,根据动能定理,电荷从等势面A运动到C的过程中 q△U=0-20………………①
电荷从等势面A运动到B的过程中 q△U=EKB一20…………②
联立①②得EKB=10J
又电荷仅受电场力在电场中运动时,根据运动定理: WAB=EKB一EKA…………③
根据电场力做功与电势能变化的关系 wAB=εA一εB…………④
联立③④得,εA+EKA=εB+EKB=恒量
又在B点εB =0所以EK+2=0+10, 解出EK=8J
 点评:讨论静电场中电荷运动的能量关系,一般都应用动能定理,但注意电势能的变化只由电场力做功决定,与其他力是否做功无关。
点评:讨论静电场中电荷运动的能量关系,一般都应用动能定理,但注意电势能的变化只由电场力做功决定,与其他力是否做功无关。
[例5]如图所示,直角三角形的斜边倾角为300,底边BC长为2L,处在水平位置,斜边AC是光滑绝缘的,在底边中点O处放置一正电荷Q,一个质量为m、电量为 q的带负电的质点从斜面顶端A沿斜边滑下,滑到斜边上的垂足D时速度为v。(将(1),(2)题正确选项前的标号填在题后括号内)
(1)在质点的运动中不发生变化的是
①动能;②电势能与重力势能之和;③动能与重力势能之和;④动能、电势能。重力势能三者之和。
A、①② B.②③ C\④ D,②
(2)质点的运动是
A.匀加速运动; B.匀减速运动; C.先加速后匀减速的运动; D.加速度随时间变化的运动
(3)该质点滑到非常接近斜边底端C点时速率vc为多少?沿斜面向下的加速度ac为多少?
解析:斜面光滑,表明无摩擦力的作用,粒子在重力、电场力、斜面弹力三者的作用下运动。重力场与静电场均是保守力场,因此在整个运动中应该是动能、电势能、重力势能三者之和为一不变量,因此第(1)题选C。
若O点应电荷O不存在,则粒子在斜面上的运动是匀加速运动,现在粒子还处在静电场中,随着粒子运动,电场力的大小、方向是逐渐变化的,因而粒子总的来说是在变力的作用下运动。由牛顿第二定律,粒于运动的加速度也是变化的,这样第(2)个选择(D),质点的运动是加速度随时间变化的运动。
质点受三个力作用,电场力f=kQq/L2,方向由C指向O点(库仑吸引);重力 mg,方向竖直向下;支持力N,方向垂直于斜面向上。由牛顿第二定律
mgsinθ一fcosθ=mac,即mgsin300一kQq/L2cos300=maC,简化得aC=½g- kQq/2mL2
kQq/2mL2
在斜面整个运动过程中电势能、动能、重力势能三者的和不变,已知质点运动到D点的速度V,则D点的电势能可求出,从几何关系容易发现,B、C、D分别到O点的距离是相等的,则BD=BC/2=BO=OC=OD,B、C、D三点在以O为圆心的同一圆周上,是O点处点电荷Q产生的电场中的等势点,所以,q由D到C的过程中电场力作功为零,由机械能守恒定律,得mgh=½mvC2一½mv2……①,其中h为质点在D点的高度,h=BDsin600=BCsin300 sin600=2L ×½× /2=
/2= L/2,得vC=
L/2,得vC= ……②,
……②,
规律方法 1、一组概念的理解与应用
电势、电势能、电场强度都是用来描述电场性质的物理,,它们之间有+分密切的联系,但也有很大区别,解题中一定注意区分,现列表进行比较
(1)电势与电势能比较:
|
|
电势φ |
电势能ε |
|
1 |
反映电场能的性质的物理量 |
荷在电场中某点时所具有的电势能 |
|
2 |
电场中某一点的电势φ的大小,只跟电场本身有关,跟点电荷无关 |
电势能的大小是由点电荷q和该点电势φ共同决定的 |
|
3 |
电势差却是指电场中两点间的电势之差,ΔU=φA-φB,取φB=0时,φA=ΔU |
电势能差Δε是指点电荷在电场中两点间的电势能之差Δε=εA-εB=W,取εB=0时,εA=Δε |
|
4 |
电势沿电场线逐渐降低,取定零电势点后,某点的电势高于零者,为正值.某点的电势低于零者,为负值 |
正点荷(十q):电势能的正负跟电势的正负相同负电荷(一q):电势能的正负限电势的正负相反 |
|
5 |
单位:伏特 |
单位:焦耳 |
|
6 |
联系:ε=qφ,w=Δε=qΔU |
(2)电场强度与电势的对比
|
|
电场强度E |
电势φ |
|
1 |
描述电场的力的性质 |
描述电场的能的性质 |
|
2 |
电场中某点的场强等于放在该点的正点电荷所受的电场力F跟正点电荷电荷量q的比值·E=F/q,E在数值上等于单位正电荷所受的电场力 |
电场中某点的电势等于该点跟选定的标准位置(零电势点)间的电势差,φ=ε/q,φ在数值上等于单位正电荷所具有的电势能 |
|
3 |
矢量 |
标量 |
|
4 |
单位:N/C;V/m |
V(1V=1J/C) |
|
5 |
联系:①在匀强电场中UAB=Ed
(d为A、B间沿电场线方向的距离).②电势沿着电场强度的方向降落 |
 [例6]如图所示,在水平桌面上放置一个由两根绝缘组成的“V”形竖直导轨,棒上各穿上一个可沿棒无摩擦滑动的,质量为m=40g,带电量为q=2×10-6C的正电荷小球(可当作点电荷),将小球从同高度的力、B由静止释放(g=10m/s2)
[例6]如图所示,在水平桌面上放置一个由两根绝缘组成的“V”形竖直导轨,棒上各穿上一个可沿棒无摩擦滑动的,质量为m=40g,带电量为q=2×10-6C的正电荷小球(可当作点电荷),将小球从同高度的力、B由静止释放(g=10m/s2)
(1)两球相距多远时速度达到最大?
(2)两球同时到达最高点时相距 L=1.8m,此时系统电势能比释放时少多少?
[解](1)设两球相距L1时速度达到最大,此时合力为零。其中一个小球受力如图所示,FA为A球受库仑力.则:
FA=mgtg450=mg…………………①
由库仑定律:FA=kq1q2/L12………②
 由①、②得:
由①、②得:
(2)两球达最高点时速度为零,设释放时离桌面高度为h1,最高点时离桌面高度为h2,则两球在上升过程的能量变化情况为:动能的变化ΔEK=0,重力势能的变化量ΔEP=2mg(h2-hl)。设电势能变化量为Δε,则由能的转化和守恒定律知:ΔEK十ΔEP+Δε=0则:Δε=-mg(h2-hl)=-2×40×10-3×10×(L/2tg450-0.05)=-0.68(J)。 即系统的电势能减少了0.68J。
1.电场中电势相等的点所组成的面为等势面.
3.电场力做功:W=qU,U为电势基,q为电量.
重力做功:W=Gh,h为高度差,G为重量.
电场力做功跟路径无关,是由初末位置的电势差与电量决定
重力做功跟路径无关,是由初末位置的高度差与重量决定.
[例1]关于电势与电势能的说法正确的是( )
A.电荷在电场中电势高的地方电势能大
B.在电场中的某点,电量大的电荷具有的电势能比电量小的电荷具有的电势能大
C.正电荷形成的电场中,正电荷具有的电势能比负电荷具有的电势能大
D.负电荷形成的电场中,正电荷具有的电势能比负电荷具有的电势能小
解析:正电荷在电势高处的电势能比电势低处的电势能大,负电荷则反之,所以A错.当具有电势为正值时,电量大的电荷具有的电势能大于电量小的电荷具有的电势能,当电势为负值,恰好相反,所以B错.正电荷形成的电场中,电势为正值,这样电势与正电荷的电量来积为正值,而负电荷在正电荷形成的电场中电势能为负值,因此C正确.负电荷形成的电场中,电势为负值,因而正电荷具有的电势能为负值,负电行具有的电势能为正值,所以D正确. 答案:CD
 点评:关于电势的正负与电势的高低参看下图8一31所示,A、B带等量的异种电荷,AO区间是正电荷形成的电场,OB区间是负电荷形成的电场.
点评:关于电势的正负与电势的高低参看下图8一31所示,A、B带等量的异种电荷,AO区间是正电荷形成的电场,OB区间是负电荷形成的电场.
[例2]将一电量为一2×10-8C的点电荷,从零电势S点移到电场中的M点,反抗电场力做功4×10-8J,则UM= ;若将该电荷从M点移到N点,电场力做功14×10-8J,则N点电势UN= ;M、N两点电势差为 .
解析:UM=W/q=4×10-8/2×10-8=2V.由于是负电荷反抗电场力做功,所以是顺着电场线移动,M点电势为负.所以UM=一2V.UN=14×10-8/2×10-8=7V.由于是电场力做功,所以负电荷是逆着电场线方向移动,N点电势比M点电势高7V,这样N点电势比S点高5V,所以UN=5V.
点评:(1)求某点电势可先求出电势差,然后根据电势差和电场力做功情况再求出该点电势.
(1) 应牢记:电场力做正功,电势能减少;电场力做负功,电势能增加.
2.电势能的变化:电场力做正功电势能减少;电场力做负功电势能增加.
重力势能变化:重力做正功重力势能减少;重力做负功重力势能增加.
1.电势能:电场中电荷具有的势能称为该电荷的电势能.电势能是电荷与所在电场所共有的。
某点相对零电势的电势差叫做该点的电势,是标量.在数值上等于单位正电荷由该点移到零电势点时电场力所做的功.由电场本身因素决定,与检验电荷无关。
点评:类似于重力场中的高度.某点相对参考面的高度差为该点的高度.
注意:(1)高度是相对的.与参考面的选取有关,而高度差是绝对的与参考面的选取无关.同样电势是相对的与零电势的选取有关,而电势差是绝对的,与零电势的选取无关.
(2)一般选取无限远处或大地的电势为零.当零电势选定以后,电场中各点的电势为定值.
(3)电场中A、B两点的电势差等于A、B的电势之差,即UAB=φA-φB,沿电场线方向电势降低.
3、 电场线的理解和应用
 [例11]如图所示,一电子沿等量异种电荷的中垂线由A-O-B匀速飞过,电子重力不计,则电子所受另一个力的大小和方向变化情况是
[例11]如图所示,一电子沿等量异种电荷的中垂线由A-O-B匀速飞过,电子重力不计,则电子所受另一个力的大小和方向变化情况是
A.先变大后变小,方向水平向左 B.先变大后变小,方向水平向右
C.先变小后变大,方向水平向左 D.先变小后变大,方向水平向右
[分析]由等量异种电荷电场线分布可知,从A到O,电场由疏到密;从O到B,电场线由密到疏,所以从A-O-B,电场强度应由小变大,再由大变小,而电场强度方向沿电场切线方向,为水平向右。由于电子处于平衡状态,所受合外力必为零,故另一个力应与电子所受电场力大小相等方向相反。电子受的电场力与场强方向相反,即水平向左,电子从A-O-B过程中,电场力由小变大,再由大变小,故另一个力方向应水平向右,其大小应先变大后变小,所以选项B正确。
试题展示
 散
电场能的性质
散
电场能的性质
知识简析 一、电势差
电荷从电场中的一点移到另一点,电场力做的功跟其电量的比值叫做这两点的电势差,U=W/q,是标量.
点评:电势差很类似于重力场中的高度差.物体从重力场中的一点移到另一点,重力做的功跟其重量的比值叫做这两点的高度差h=W/G.
2、 电场强度的理解和应用
[例8]长木板AB放在水平面上如图所示,它的下表面光滑而上表面粗糙,一个质量为m、电量为q的小物块C从A端以某一初速起动向右滑行。当存在向下的匀强电场时,C恰能滑到B端,当此电场改为向上时,C只能滑到AB的中点,求此电场的场强。
 [解析]当电场方向向上时,物块c只能滑到AB中点,说明此时电场力方向向下,可知物块C所带电荷的电性为负。
[解析]当电场方向向上时,物块c只能滑到AB中点,说明此时电场力方向向下,可知物块C所带电荷的电性为负。
电场方向向下时有:μ(mg-qE)L=½mv02一(m+M)v2 mv0=( m十M)v
电场方向向上时有:μ(mg+qE)L/2=½mv02一(m+M)v2, mv0=( m十M)v
则mg-qE =(mg+qE),得E=mg/3q
 [例9]如图在场强为E的匀强电场中固定放置两个带电小球1和2,它们的质量相等,电荷分别为q1和-q2.(q1≠q2).球1和球2的连线平行于电场线,如图.现同时放开1球和2球,于是它们开始在电场力的作用下运动,如果球1和球2之间的距离可以取任意有限值,则两球刚被放开时,它们的加速度可能是(
ABC )
[例9]如图在场强为E的匀强电场中固定放置两个带电小球1和2,它们的质量相等,电荷分别为q1和-q2.(q1≠q2).球1和球2的连线平行于电场线,如图.现同时放开1球和2球,于是它们开始在电场力的作用下运动,如果球1和球2之间的距离可以取任意有限值,则两球刚被放开时,它们的加速度可能是(
ABC )
A、大小不等,方向相同; B、大小不等,方向相反;
C、大小相等,方向相同; D、大小相等,方向相反;
解析:球1和球2皆受电场力与库仑力的作用,取向右方向为正方向,则有 由于两球间距不确定,故F库不确定
由于两球间距不确定,故F库不确定
若q1E-F库>0, F库-q2E>0,且q1E-F库≠F库-q2E,则A正确;
若q1E-F库>0, F库-q2E <0,且q1E-F库≠F库-q2E ,则B正确;
若q1E-F库=F库-q2E ,则C正确;
若q1E-F库≠F库-q2E ,则q1= q2与题意不符,D错误;
 [例10]半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m,带正电的珠子,空间存在水平向右的匀强电场,如图所示,珠子所受静电力是其重力的3/4,将珠子从环上最低位置A点由静止释放,则珠子所能获得的最大动能Ek为多少?
[例10]半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m,带正电的珠子,空间存在水平向右的匀强电场,如图所示,珠子所受静电力是其重力的3/4,将珠子从环上最低位置A点由静止释放,则珠子所能获得的最大动能Ek为多少?
 解析:设该珠子的带电量为q,电场强度为E.珠子在运动过程中受到三个力的作用,其中只有电场力和重力对珠子做功,其合力大小为:
解析:设该珠子的带电量为q,电场强度为E.珠子在运动过程中受到三个力的作用,其中只有电场力和重力对珠子做功,其合力大小为:
设F与竖直方向的夹角为θ,如图所示,则
把这个合力等效为复合场,此复合场为强度 此复合场与竖直方向夹角为θ,珠予沿园环运动,可以类比于单摆的运动,运动中的动能最大位置是“最低点”,由能的转化及守恒可求出最大的动能为:Ekm=mg/r(1-cosθ)
此复合场与竖直方向夹角为θ,珠予沿园环运动,可以类比于单摆的运动,运动中的动能最大位置是“最低点”,由能的转化及守恒可求出最大的动能为:Ekm=mg/r(1-cosθ) 
思考:①珠子动能最大时对圆环的压力多大?
②若要珠子完成一个完整的圆周运动,在A点释放时,是否要给珠子一个初速度?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com