
3.原子光谱
在人们了解原子结构以前,就发现了气体光谱。和白光形成的连续光谱不同,稀薄气体通电后发出的光得到的光谱是不连续的几条亮线,叫做线状谱。
因为各种原子的能级是不同的,它们的线状谱也就不会完全相同。因此把这些线状谱叫做原子光谱。利用原子光谱可以鉴别物质,分析物体的化学组成。
玻尔理论能够很好地解释氢的原子光谱。根据hν=Em-En计算出的频率跟实验中观察到的线状谱对应的频率恰好相同。
2.光子的发射和接收
原子处于基态时最稳定。处于激发态时会自发地向较低能级跃迁,经过一次或几次跃迁到达基态。跃迁时以光子的形式放出能量。所放出光子的频率满足:hγ=Em-En
原子吸收了光子后从低能级跃迁到高能级,或者被电离。
处于基态或较低激发态的原子只能吸收两种光子:一种是能量满足hγ=Em-En的光子,一种是能量大于该能级电离能的光子。
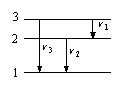 [例6]用光子能量为E的单色光照射容器中处于基态的氢原子。停止照射后,发现该容器内的氢能释放出三种不同频率的光子,它们的频率由低到高依次为ν1、ν2、ν3,由此可知,开始用来照射容器的单色光的光子能量可以表示为:①hν1;②hν3;③h(ν1+ν2);④h(ν1+ν2+ν3)
以上表示式中
[例6]用光子能量为E的单色光照射容器中处于基态的氢原子。停止照射后,发现该容器内的氢能释放出三种不同频率的光子,它们的频率由低到高依次为ν1、ν2、ν3,由此可知,开始用来照射容器的单色光的光子能量可以表示为:①hν1;②hν3;③h(ν1+ν2);④h(ν1+ν2+ν3)
以上表示式中
A.只有①③正确 B.只有②正确
C.只有②③正确 D.只有④正确
解:该容器内的氢能够释放出三种不同频率的光子,说明这时氢原子处于第三能级。根据玻尔理论应该有hν3=E3- E1,hν1=E3- E2,hν2=E2- E1,可见hν3= hν1+ hν2= h(ν1+ν2),所以照射光子能量可以表示为②或③,答案选C。
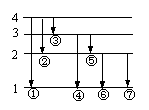 [例7]现有1200个氢原子被激发到量子数为4的能级上,若这些受激氢原子最后都回到基态,则在此过程中发出的光子总数是多少?假定处在量子数为n的激发态的氢原子跃迁到各较低能级的原子数都是处在该激发态能级上的原子总数的
[例7]现有1200个氢原子被激发到量子数为4的能级上,若这些受激氢原子最后都回到基态,则在此过程中发出的光子总数是多少?假定处在量子数为n的激发态的氢原子跃迁到各较低能级的原子数都是处在该激发态能级上的原子总数的 。
。
A.1200 B.2000 C.2200 D.24 00
解:画出示意图,分步计算,不难得出结论①400个,②400个,③400个,④200个,⑤200个,⑥200个,⑦400个,共2200个。
初中介绍了卢瑟福提出的原子的核式结构模型。认为电子绕核做圆周运动,好比地球绕太阳做圆周运动。
研究表明,卢瑟福的核式结构模型和经典电磁理论有矛盾:
按照经典电磁理论:⑴电子绕核做圆周运动会向外辐射同频率的电磁波,能量将减小,原子将会不稳定;⑵电子旋转半径减小的同时,频率将增大,因此辐射的电磁波频率也应该是连续变化的。事实上原子是稳定的,原子辐射的电磁波的频率也是不变的。
1.玻尔理论
为解决这个矛盾,玻尔将量子理论引入原子结构理论,大胆提出了三条假设,创建了玻尔原子模型。
①能量定态假设:原子只能处于一系列的不连续的能量状态中,在这些状态中原子是稳定的,电子虽然绕核运动,但并不向外辐射能量,这些状态叫定态。
②原子跃迁假设:原子从一定态跃迁到另一种定态,它要辐射(或吸收)一定频率的光子,光子的能量由这两种定态的能量差值决定:即:hν=Em-En
 ③轨道量子化假设:原子的不同能量状态跟电子沿不同的圆形轨道绕核运动相对应,原子的定态是不连续的,因此电子所处的可能轨道的分布也是不连续的。
③轨道量子化假设:原子的不同能量状态跟电子沿不同的圆形轨道绕核运动相对应,原子的定态是不连续的,因此电子所处的可能轨道的分布也是不连续的。
对氢原子:轨道量子化 , r1=0.53×10-10m n叫量子数
能量量子化  , E1=--13.6eV,这些能量值叫能级。能量最低的状态(量子数n=1)叫基态,其他状态叫激发态。
, E1=--13.6eV,这些能量值叫能级。能量最低的状态(量子数n=1)叫基态,其他状态叫激发态。
根据玻尔理论画出了氢原子的能级图。
对于宏观质点,只要知道它在某一时刻的位置和速度以及受力情况,就可以应用牛顿定律确定该质点运动的轨道,算出它在以后任意时刻的位置和速度。
对电子等微观粒子,牛顿定律已不再适用,因此不能用确定的坐标描述它们在原子中的位置。玻尔理论中说的“电子轨道”实际上也是没有意义的。更加彻底的量子理论认为,我们只能知道电子在原子核附近各点出现的概率的大小。在不同的能量状态下,电子在各个位置出现的概率是不同的。如果用疏密不同的点子表示电子在各个位置出现的概率,画出图来,就像一片云雾一样,可以形象地称之为电子云。
物质分为两大类:实物和场。既然作为场的光有粒子性,那么作为粒子的电子、质子等实物是否也具有波动性?德布罗意由光的波粒二象性的思想推广到微观粒子和任何运动着的物体上去,得出物质波的概念:任何一个运动着的物体都有一种波与它对应,该波的波长λ=h/p。
人们又把这种波叫做德布罗意波。物质波也是概率波。
[例4]试估算一个中学生在跑百米时的德布罗意波的波长。
解:估计一个中学生的质量m≈50kg ,百米跑时速度v≈7m/s ,则 m
m
由计算结果看出,宏观物体的物质波波长非常小,所以很难表现出其波动性。
[例5] 为了观察到纳米级的微小结构,需要用到分辨率比光学显微镜更高的电子显微镜。下列说法中正确的是
A.电子显微镜所利用电子物质波的波长可以比可见光短,因此不容易发生明显衍射
B.电子显微镜所利用电子物质波的波长可以比可见光长,因此不容易发生明显衍射
C.电子显微镜所利用电子物质波的波长可以比可见光短,因此更容易发生明显衍射
D.电子显微镜所利用电子物质波的波长可以比可见光长,因此更容易发生明显衍射
解:为了观察纳米级的微小结构,用光学显微镜是不可能的。因为可见光的波长数量级是10-7m,远大于纳米,会发生明显的衍射现象,因此不能精确聚焦。如果用很高的电压使电子加速,使它具有很大的动量,其物质波的波长就会很短,衍射的影响就小多了。因此本题应选A。
4.光在传播过程中往往表现出波动性;在与物质发生作用时往往表现为粒子性;光既具有波动性,又具有粒子性,为说明光的一切行为,只能说光具有波粒二象性.
说明:光的波粒二象性可作如下解释:
(1)既不可把光当成宏观观念中的波,也不可把光当成微观观念中的粒子.
(2)大量光子产生的效果往往显示出波动性,个别光子产生的效果往往显示出粒子性;频率超低的光波动性越明显,频率越高的光粒子性越明显.
(3)光在传播过程中往往显示波动性,在与物质作用时往往显示粒子性.
(4)由E=hγ,p =h/λ看出,光的波动性和粒子性并不矛盾:表示粒子性的粒子能量和动量的计算式中都含有表示波的特征的物理量--频率γ和波长λ。
(5)由以上两式和波速公式c=λγ还可以得出:E = p c
(6)对干涉现象理解:
①对亮条纹的解释:波动说:同频率的两列波到达亮纹处振动情况相同;粒子说:光子到达的几率大的地方。
②对暗条纹的解释:波动说:同频率的两列波到达暗纹振动情况相反;粒子说:光子到达的几率小的地方。
3、个别光子的行为体现为粒子性;频率越高、波长越短的光,其粒子性越显著.
2、 大量光子的传播规律体现为波动性;频率低、波长长的光,其波动性越显著.
1、 干涉、衍射和偏振表明光是一种波;光电效应和康普顿效应表明光是一种粒子;因此现代物理学认为:光具有波粒二象性。
 光子在介质中和物质微粒相互作用,可能使得光的传播方向转向任何方向(不是反射),这种现象叫做光的散射。
光子在介质中和物质微粒相互作用,可能使得光的传播方向转向任何方向(不是反射),这种现象叫做光的散射。
在研究电子对X射线的散射时发现:有些散射波的波长比入射波的波长略大。康普顿认为这是因为光子不仅有能量,也具有动量。实验结果证明这个设想是正确的。因此康普顿效应也证明了光具有粒子性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com