(三)例题分析：

例1．已知函数的定义域为，函数的定义域为，则

　　　 　　　　　　　　　( 　)

解法要点：，，

令且，故．

例2．(1)已知，求；

(2)已知，求；

(3)已知是一次函数，且满足，求；

(4)已知满足，求．

解：(1)∵，

∴(或)．

(2)令()，则，∴，∴．

(3)设，

则，

∴，，∴．

(4)　 ①，　　　 把①中的换成，得　　 ②，

①②得，∴．

注：第(1)题用配凑法；第(2)题用换元法；第(3)题已知一次函数，可用待定系数法；第(4)题用方程组法．

例3．设函数，

(1)求函数的定义域；

解：(1)由，解得　　 ①

当时，①不等式解集为；当时，①不等式解集为，

∴的定义域为．

(二)主要方法：

1．求函数解析式的题型有：

(1)已知函数类型，求函数的解析式：待定系数法；

(2)已知求或已知求：换元法、配凑法；

(3)已知函数图像，求函数解析式；

(4)满足某个等式，这个等式除外还有其他未知量，需构造另个等式：解方程组法；

(5)应用题求函数解析式常用方法有待定系数法等．

2．求函数定义域一般有三类问题：

(1)给出函数解析式的：函数的定义域是使解析式有意义的自变量的取值集合；

(2)实际问题：函数的定义域的求解除要考虑解析式有意义外，还应考虑使实际问题有意义；

(3)已知的定义域求的定义域或已知的定义域求的定义域：

①掌握基本初等函数(尤其是分式函数、无理函数、对数函数、三角函数)的定义域；

②若已知的定义域，其复合函数的定义域应由解出．

(一)主要知识：1．函数解析式的求解；2．函数定义域的求解．

(四)巩固练习：

1．给定映射，点的原象是　　　

2．下列函数中，与函数相同的函数是　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　 (　 　)

3．设函数，则＝．

(三)例题分析：

例1．(1)，，；

(2)，，；

(3)，，．

上述三个对应　　 是到的映射．

例2．已知集合，映射，在作用下点的象是，则集合　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

解法要点：因为，所以．

例3．矩形的长，宽，动点、分别在、上，且，(1)将的面积表示为的函数，求函数的解析式；

(2)求的最大值．

解：(1)

．

∵，∴，

∴函数的解析式：；

(2)∵在上单调递增，∴，即的最大值为．

例4．函数对一切实数，均有成立，且，

(1)求的值；

(2)对任意的，，都有成立时，求的取值范围．

解：(1)由已知等式，令，得，

又∵，∴．

(2)由，令得，由(1)知，∴．

∵，∴在上单调递增，∴．

要使任意，都有成立，

当时，,显然不成立．

当时，，∴，解得

∴的取值范围是．

(二)主要方法：

1．对映射有两个关键点：一是有象，二是象惟一，缺一不可；

2．对函数三要素及其之间的关系给以深刻理解，这是处理函数问题的关键；

3．理解函数和映射的关系，函数式和方程式的关系．

(一)主要知识：

1．对应、映射、像和原像、一一映射的定义；

2．函数的传统定义和近代定义；

3．函数的三要素及表示法．

　　 (1) 我国共有______个民族，其中人口最多的是_________，_________个少数民族，人　 口最多的少数民族是____________。

　 (2) 汉族的分布遍及全国各地，以___________和__________最为集中。

　 (3) 少数民族的分布相对分散，各少数民族主要分布在_________、_________和__________地区。各民族分布具有“_____________________”的特点。

　 (4) 各民族有独特的风俗习惯、文化艺术和传统的体育活动，如傣族_____________、蒙古族_____________大会、___________的长鼓舞、彝族的火把节等。

4、人口国策： 实行计划生育　 内容：控制人口数量，提高人口素质 。

例题1。实行计划生育以来，我国每年净增人口数量仍在一千万以上，其最主要的原因是

　　　 A．人口死亡率低　　　　 　B．人口出生率高

　　　 C．人口基数大　　　　　　 D．人口自然增长率高

例题2. 读我国人口增长曲线图(如图3所示)，回答下列问题：

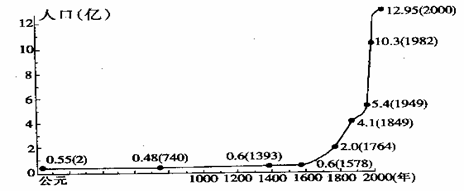
　(1)旧中国在较长的历史时期，由于战争、疫病等原因，死亡率____________，人口增长_________。　　

(2)新中国成立后，人口增长基本上呈_______线上升趋势。

(3)人既是生产者，又是_________者，人口数量的增长应与_____、_____的发展相适应，与______、_______相协调，为此我国政府把实行______作为一项长期的基本国策，控制人口________，提高人口_______，具体要求是：________、晚育、少生、_________。

3、人口分布特点：人口分布(不均)(黑河-腾冲线)。