19. 解：(1)证明：∵，且数列各项均为正数，

∴(常数)………………………………………2分

∴数列为等差数列，首项，公差，

∴，　　　　　　 ∴…………………5分

(2)∵，　　　　　 ∴

∴……………………………8分

∵，∴，

∵函数在上是增函数，∴，

综上所述：。…………………………………………………………12分

18. 解：(1)记“甲投篮投中”的事件为，“乙投篮投中”的事件为，

则

其概率为　 ………………………………………6分

(2)解法一：乙至多投篮两次，分三种情况：①乙一次也没有投篮；②乙只投篮一次；③乙投篮两次

对①其概率为 ………………………………………8分

对②其概率为

　　　　　　 …………………………………10分

对③其概率为

乙至多投篮两次的概率为　 ……………………12分

解法二：考虑对立面，即乙投篮三次的概率为………………………………9分

乙至多投篮两次的概率为……………………………………12分

17.解：

...............................2分

.....................................................5分

，，即……………………………8分

又

……………………………………………10分

于是………………………………12分

13．1　 14． 15．等腰　 16．①②④

1．B　 2．C　 3．D　 4．A　 5．D　6．C　 7．B　 8．C　 9．C　 10．D　11．A　 12．A

22．(本题满分14分)已知直线过椭圆E:的右焦点，且与E相交于两点.

(1)设(为原点)，求点的轨迹方程；

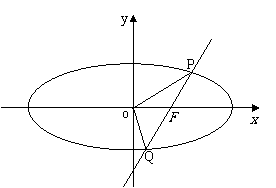(2)若直线的倾斜角为，求的值.

高三第一轮复习训练题

数学(十九) (文科综合卷一)参考答案

21．(本题满分12分)已知函数.　

(1)若在[0，2]上是增函数，是方程的一个实根，求证：；

(2)若的图象上任意不同两点的连线斜率小于1，求实数的取值范围.

20．(本题满分12分)如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD是正三角形，且

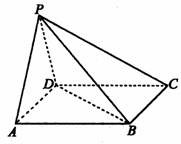平面PAD⊥底面ABCD.

(1)求证：AB⊥平面PAD

(2)求直线PC与底面ABCD所成角的大小；

(3)设AB=1，求点D到平面PBC的距离.

19．(本题满分12分)已知各项均为正数的数列满足：，。

(1)证明数列为等差数列，并求；

(2)设，数列的前项和为，求证：。

18．(本题满分12分)甲、乙两人进行投篮游戏，投篮者若投中则继续投篮，否则由对方投篮，第一次由甲投篮；已知每次投篮甲、乙投中的概率分别为、，在前次投篮中

(1)求第三次由甲投篮的概率；

(2)求乙至多投篮两次的概率。