
1.下列对“儒家文化是否存在的四个标志”的表述,不正确的一项是 ( )
A.是否有自觉继承文化精髓的传人。
B.文化赖以生存的基本的社会结构是否存在。
C.文化的基本价值取向是否影响人们在生活中的选择。
D.文化的独特语言是否存在于人们的话语和艺术形式之中。
[答案]C
[解析] “是否影响”表述错误,原文是“已基本上不能影响”。
4.实数与数轴上的点是一一对应的。每一个实数都可以用数轴上的一个点来表示;反之数轴上的每一个点又都表示一个实数。
5.实数的相反数:如果a表示一个正实数,-a就表示一个负实数。又如果a表示一个负实数,则-a表示一个正实数。a与-a互为相反数。0的相反数仍是0。如  与-
与-  ,
,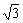 与-
与-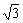 ,m与-m…均互为相反数。
6.实数的绝对值:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。即如果a是一个实数,则有
|a|=
,m与-m…均互为相反数。
6.实数的绝对值:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。即如果a是一个实数,则有
|a|=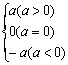 例如,|-
例如,|-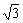 |=
|=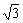 ,|-
,|-  |=
|=  ,|
,|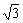 |=
|=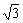 ,|
,|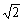 -
-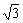 |=-(
|=-(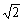 -
-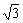 )=
)=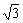 -
-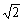 …
注意:-a(a<0)是正数,例如:-(
…
注意:-a(a<0)是正数,例如:-(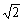 -
-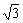 )
7.有理数的运算律和运算性质在实数范围内仍然适用。
三、例题分析:
例1.找出下列各数中的无理数:-5,3.1416,
)
7.有理数的运算律和运算性质在实数范围内仍然适用。
三、例题分析:
例1.找出下列各数中的无理数:-5,3.1416, 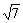 , -
, -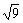 ,
,  ,
,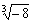 ,
,  ,-
,-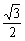 ,0.808008…,
0.
,0.808008…,
0.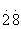 ,
,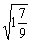 ,
,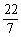 。
解:无理数是无限不循环小数。3.1416是有限小数;0.
。
解:无理数是无限不循环小数。3.1416是有限小数;0.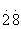 是无限循环小数;-5,-
是无限循环小数;-5,-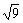 =-3,
=-3,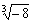 =-2是整数;
=-2是整数;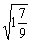 =
=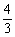 ,
,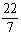 是分数,所以它们都是有理数。
那么无理数有:
是分数,所以它们都是有理数。
那么无理数有: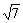 ,
,  ,
,  ,-
,-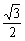 ,0.808008…,因为它们都是无限不循环小数。
注意:0.808008…是无限不循环小数,只是数字有规律,但不是循环小数,两者区分开。
例2.比较下列各组数的大小:
(1) -
,0.808008…,因为它们都是无限不循环小数。
注意:0.808008…是无限不循环小数,只是数字有规律,但不是循环小数,两者区分开。
例2.比较下列各组数的大小:
(1) -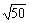 与-7;(2)
与-7;(2)  与
与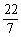 ;(3)
;(3) 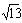 -
-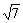 与
与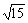 -
-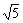 ;(4)把下列各数按照由小到大的顺序,用不等号连结起来:4, -3, -4
;(4)把下列各数按照由小到大的顺序,用不等号连结起来:4, -3, -4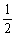 ,1.414,
0, 0.8, -
,1.414,
0, 0.8, -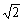 ,
,  , -|4
, -|4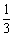 |,
|, 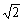 分析:实数比较大小是综合性较强的题目,往往需要把无理数用近似的有理数代替,再用有理数比较大小的方法来进行比较;有些需要用平方的方法,平方后再比较大小;有时还需找中介值等等。
解:
(1)变成统一形式
∵ |-
分析:实数比较大小是综合性较强的题目,往往需要把无理数用近似的有理数代替,再用有理数比较大小的方法来进行比较;有些需要用平方的方法,平方后再比较大小;有时还需找中介值等等。
解:
(1)变成统一形式
∵ |-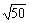 |=
|=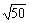 ,
|-7|=7=
,
|-7|=7=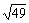 <
<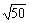 ∴ -
∴ -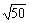 <-7 (两个负数比较大小,绝对值大的反而小)
(2)利用近似数
∵
<-7 (两个负数比较大小,绝对值大的反而小)
(2)利用近似数
∵  =3.14159…,
=3.14159…, 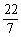 =3.1428…
∴
=3.1428…
∴  <
<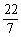 (3) 用平方的方法:
(
(3) 用平方的方法:
( -
- )2=13+7-2
)2=13+7-2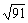 =20-2
=20-2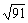 (
(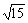 -
-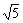 )2=20-2
)2=20-2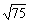 ∵ 20-2
∵ 20-2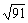 <20-2
<20-2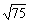 即(
即( -
-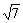 )2<(
)2<(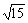 -
-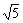 )2
且
)2
且 -
-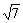 >0,
>0, 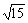 -
-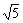 >0
∴
>0
∴  -
-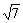 <
<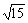 -
-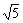 (4) 由 -
(4) 由 -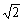 =-1.414…,
=-1.414…, 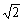 =-1.414…, -|4
=-1.414…, -|4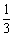 |=-4
|=-4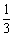 ,
,  =3.14159…,把所有的数在数轴上找到与它们对应的点(或者变成近似数),从左到右便可得到:
-4
=3.14159…,把所有的数在数轴上找到与它们对应的点(或者变成近似数),从左到右便可得到:
-4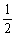 <-|4
<-|4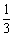 |<-3<-
|<-3<-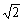 <0<0.8<1.414<
<0<0.8<1.414<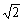 <
<  <4
<4
例3.化简下列各式:
(1) |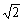 -1.4
-1.4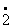 | (2) |
| (2) |  -3.142| (3) |
-3.142| (3) |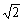 -
-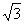 | (4) |x-|x-3|| (x≤3)
(5) |x2+6x+10|
分析:要正确去掉绝对值符号,就要弄清绝对值符号内的数是正数、负数还是零,然后根据绝对值的定义正确去掉绝对值。
解:
(1) ∵
| (4) |x-|x-3|| (x≤3)
(5) |x2+6x+10|
分析:要正确去掉绝对值符号,就要弄清绝对值符号内的数是正数、负数还是零,然后根据绝对值的定义正确去掉绝对值。
解:
(1) ∵ 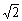 =1.414…<1.4
=1.414…<1.4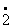 ∴ |
∴ |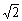 -1.4
-1.4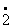 |=1.4
|=1.4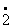 -
-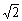 (2) ∵
(2) ∵  =3.14159…<3.142
∴ |
=3.14159…<3.142
∴ |  -3.142|=3.142-
-3.142|=3.142-  (3) ∵
(3) ∵ 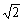 <
<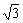 , ∴ |
, ∴ |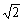 -
-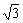 |=
|=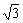 -
-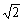 (4) ∵ x≤3, ∴ x-3≤0,
∴ |x-|x-3||=|x-(3-x)|
=|2x-3| =
(4) ∵ x≤3, ∴ x-3≤0,
∴ |x-|x-3||=|x-(3-x)|
=|2x-3| =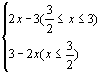 说明:这里对|2x-3|的结果采取了分类讨论的方法,我们对
说明:这里对|2x-3|的结果采取了分类讨论的方法,我们对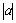 =
=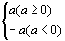 这个绝对值的基本概念要有清楚的认识,并能灵活运用。
(5) |x2+6x+10|=|x2+6x+9+1|=|(x+3)2+1|
∵ (x+3)2≥0, ∴ (x+3)2+1>0
∴ |x2+6x+10|=
x2+6x+10
例4.计算下列各式:
(1)
这个绝对值的基本概念要有清楚的认识,并能灵活运用。
(5) |x2+6x+10|=|x2+6x+9+1|=|(x+3)2+1|
∵ (x+3)2≥0, ∴ (x+3)2+1>0
∴ |x2+6x+10|=
x2+6x+10
例4.计算下列各式:
(1)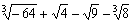 (2)
(2)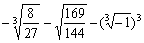 (3)
(3)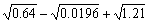 (4)0.2
(4)0.2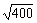 -0.7
-0.7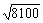 解:
(1)
解:
(1)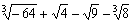 =-4+2-3-2=-7
(2)
=-4+2-3-2=-7
(2)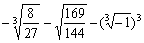 =-
=-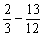 +1
=-
+1
=-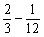 =-
=-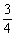 (3)
(3)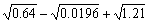 =0.8-0.14+1.1=1.76
(4)0.2
=0.8-0.14+1.1=1.76
(4)0.2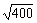 -0.7
-0.7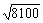 =0.2×20-0.7×90=4-63=-59
例5.已知(x-6)2+
=0.2×20-0.7×90=4-63=-59
例5.已知(x-6)2+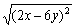 +|y+2z|=0,求(x-y)3-z3的值。
解:∵ (x-6)2+
+|y+2z|=0,求(x-y)3-z3的值。
解:∵ (x-6)2+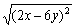 +|y+2z|=0
且(x-6)2≥0,
+|y+2z|=0
且(x-6)2≥0, 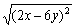 ≥0, |y+2z|≥0,
几个非负数的和等于零,则必有每个加数都为0。
∴
≥0, |y+2z|≥0,
几个非负数的和等于零,则必有每个加数都为0。
∴ 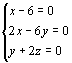 解这个方程组得
解这个方程组得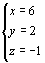 ∴ (x-y)3-z3=(6-2)3-(-1)3=64+1=65
例6.已知:
∴ (x-y)3-z3=(6-2)3-(-1)3=64+1=65
例6.已知: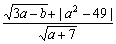 =0,求实数a, b的值。
分析:已知等式左边分母
=0,求实数a, b的值。
分析:已知等式左边分母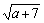 不能为0,只能有
不能为0,只能有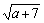 >0,则要求a+7>0,分子
>0,则要求a+7>0,分子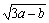 +|a2-49|=0,由非负数的和的性质知:3a-b=0且a2-49=0,由此得不等式组
+|a2-49|=0,由非负数的和的性质知:3a-b=0且a2-49=0,由此得不等式组 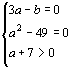 从而求出a, b的值。
解:由题意得
从而求出a, b的值。
解:由题意得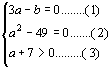 由(2)得 a2=49 ∴ a=±7
由(3)得 a>-7, ∴ a=-7不合题意舍去。
∴ 只取a=7
把a=7代入(1)得b=3a=21
∴ a=7, b=21为所求。
例7.有一个边长为11cm的正方形和一个长为13cm,宽为8cm的矩形,要作一个面积为这两个图形的面积之和的正方形,问边长应为多少cm。
解:设新正方形边长为xcm,
根据题意得 x2=112+13×8
∴ x2=225
∴ x=±15
∵ 边长为正,∴ x=-15不合题意舍去,
∴ 只取x=15(cm)
答:新的正方形边长应取15cm。
四、练习:
(一)判断正误:
(1)带根号的数都是无理数( )
(2)不带根号的数一定是有理数( )
(3)无限小数都是无理数( )
(4)无理数一定是无限不循环小数( )
(5)有理数与数轴上的点一一对应( )
(6)最小的实数是零,最大的实数不存在( )
(7)无理数加无理数的和是无理数( )
(8)有理数加无理数的和是无理数( )
(9)有理数乘无理数的积是无理数( )
(10)无理数乘无理数的积是无理数( )
(二)填空:
(1) |x-y+2|与
由(2)得 a2=49 ∴ a=±7
由(3)得 a>-7, ∴ a=-7不合题意舍去。
∴ 只取a=7
把a=7代入(1)得b=3a=21
∴ a=7, b=21为所求。
例7.有一个边长为11cm的正方形和一个长为13cm,宽为8cm的矩形,要作一个面积为这两个图形的面积之和的正方形,问边长应为多少cm。
解:设新正方形边长为xcm,
根据题意得 x2=112+13×8
∴ x2=225
∴ x=±15
∵ 边长为正,∴ x=-15不合题意舍去,
∴ 只取x=15(cm)
答:新的正方形边长应取15cm。
四、练习:
(一)判断正误:
(1)带根号的数都是无理数( )
(2)不带根号的数一定是有理数( )
(3)无限小数都是无理数( )
(4)无理数一定是无限不循环小数( )
(5)有理数与数轴上的点一一对应( )
(6)最小的实数是零,最大的实数不存在( )
(7)无理数加无理数的和是无理数( )
(8)有理数加无理数的和是无理数( )
(9)有理数乘无理数的积是无理数( )
(10)无理数乘无理数的积是无理数( )
(二)填空:
(1) |x-y+2|与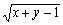 互为相反数,则x=_______, y=_______.
(2) |x|=
互为相反数,则x=_______, y=_______.
(2) |x|=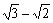 , 则x=________.
(3)
, 则x=________.
(3) 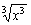 =2, 则x=________;若
=2, 则x=________;若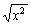 =3, 则x=_______.
(4) 若0≤x≤1, 则
=3, 则x=_______.
(4) 若0≤x≤1, 则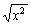 +
+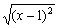 =____________
(5) 如果分式
=____________
(5) 如果分式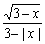 有意义,则x的取值范围是__________
(三)已知
有意义,则x的取值范围是__________
(三)已知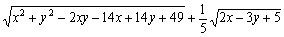 =0,试求x2-y2的值。
(四)已知:x2+y2+4x-6y+13=0,求x2+y的平方根。
练习参考答案:
(一)判断正误:
(1)×(反例:
=0,试求x2-y2的值。
(四)已知:x2+y2+4x-6y+13=0,求x2+y的平方根。
练习参考答案:
(一)判断正误:
(1)×(反例: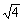 =2) (2)× (反例:p) (3)× (4)√
(5)× (6)× (反例:
=2) (2)× (反例:p) (3)× (4)√
(5)× (6)× (反例: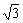 +(-
+(-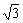 )=0) (7) √ (8)√
(9)× (反例:0×
)=0) (7) √ (8)√
(9)× (反例:0×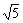 =0) (10)× (反例:
=0) (10)× (反例: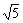 ×
×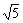 =5)
(二)填空:
(1)-
=5)
(二)填空:
(1)-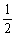 ;
;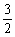 (2)±(
(2)±(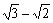 ) (3)2;±3 (4)1 (5)x<3且x≠-3
(三)
解:∵ x2+y2-2xy-14x+14y+49=(x-y)2-14(x-y)+49=(x-y-7)2
根据题意得
) (3)2;±3 (4)1 (5)x<3且x≠-3
(三)
解:∵ x2+y2-2xy-14x+14y+49=(x-y)2-14(x-y)+49=(x-y-7)2
根据题意得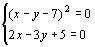 即
即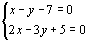 解这个方程组得
解这个方程组得 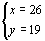 ∴ x2-y2=(x+y)(x-y)=(26+19)(26-19)=45×7=315
(四)
解:∵ x2+y2+4x-6y+13=0
而x2+y2+4x-6y+13=x2+4x+4+y2-6y+9
=(x+2)2+(y-3)2
∴ (x+2)2+(y-3)2=0
∵ (x+2)2≥0, (y-3)2≥0
∴
∴ x2-y2=(x+y)(x-y)=(26+19)(26-19)=45×7=315
(四)
解:∵ x2+y2+4x-6y+13=0
而x2+y2+4x-6y+13=x2+4x+4+y2-6y+9
=(x+2)2+(y-3)2
∴ (x+2)2+(y-3)2=0
∵ (x+2)2≥0, (y-3)2≥0
∴ 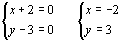 ∴ x2+y=4+3=7
∴ x2+y的平方根为±
∴ x2+y=4+3=7
∴ x2+y的平方根为±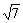
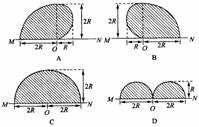
2. (05全国卷)如图,在一水平放置的平板MN的上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向里。许多质量为m带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔O射入磁场区域。不计重力,不计粒子间的相互影响。下图中阴影部分表示带电粒子可能经过的区域,其中R=mv/Bq哪个图是正确的? ( )
(05全国卷)如图,在一水平放置的平板MN的上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向里。许多质量为m带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔O射入磁场区域。不计重力,不计粒子间的相互影响。下图中阴影部分表示带电粒子可能经过的区域,其中R=mv/Bq哪个图是正确的? ( )
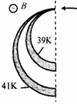 测定同位素组成的装置里(质谱仪),原子质量Al=39和A2=41钾的单价离子先在电场里加速,接着进入垂直离子运动方向的均匀磁场中(如图).在实验过程中由于仪器不完善,加速电压在乎均值U0附近变化±△U.求需要以多大相对精确度
测定同位素组成的装置里(质谱仪),原子质量Al=39和A2=41钾的单价离子先在电场里加速,接着进入垂直离子运动方向的均匀磁场中(如图).在实验过程中由于仪器不完善,加速电压在乎均值U0附近变化±△U.求需要以多大相对精确度 维持加速电压值,才能使钾同位素束不发生覆盖?
维持加速电压值,才能使钾同位素束不发生覆盖?
1.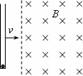 (08淮阴中学月考)如图所示,下端封闭、上端开口、内壁光滑的细玻璃管竖直放置,管底有一带电的小球。整个装置以水平向右的速度匀速运动,垂直于磁场方向进入方向水平的匀强磁场,由于外力的作用,玻璃管在磁场中的速度保持不变,最终小球从上端开口飞出,小球的电荷量始终保持不变,则从玻璃管进入磁场到小球运动到上端开口的过程中( )
(08淮阴中学月考)如图所示,下端封闭、上端开口、内壁光滑的细玻璃管竖直放置,管底有一带电的小球。整个装置以水平向右的速度匀速运动,垂直于磁场方向进入方向水平的匀强磁场,由于外力的作用,玻璃管在磁场中的速度保持不变,最终小球从上端开口飞出,小球的电荷量始终保持不变,则从玻璃管进入磁场到小球运动到上端开口的过程中( )
A.洛仑兹力对小球做正功
B.洛仑兹力对小球不做功
C.小球运动轨迹是抛物线
D.小球运动轨迹是直线
2.粒子在磁场中运动时间的确定:利用回旋角(即圆心角α)与弦切角的关系,或者利用四边形内角和等于360°,计算出圆心角α的大小,由公式t=αT/360°,可求出粒子在磁场中的运动时间。
[例3](07丹阳)如图所示,在一匀强磁场中有三个带电粒子,其中1和2为质子、3为α粒子的径迹.它们在同一平面内沿逆时针方向作匀速圆周 运动,三者轨道半径r1>r2>r3,并相切于P点.设T、v、a、t分别表示它们作圆周运动的周期、线速度、向心加速度以及各自从经过P点算起到第一次通过图中虚线MN所经历的时间,则( )
运动,三者轨道半径r1>r2>r3,并相切于P点.设T、v、a、t分别表示它们作圆周运动的周期、线速度、向心加速度以及各自从经过P点算起到第一次通过图中虚线MN所经历的时间,则( )
A. B.
B.
C. D.
D.
导示:  ,故A正确。
,故A正确。 ,故B错。
,故B错。 ,故C正确。1与2轨迹比较,1的圆心角小,
,故C正确。1与2轨迹比较,1的圆心角小, ,3的圆心角最大,而α粒子的周期又是最大,所以D正确。答案为A C D。
,3的圆心角最大,而α粒子的周期又是最大,所以D正确。答案为A C D。
类型四注意圆周运动中有关对称规律
如从同一边界射入的粒子,从同一边界射出时,速度与边界的夹角相等;在圆形磁场区域内.沿径向射入的粒子,必沿径向射出等等。
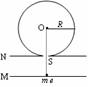 [例2]( 06连云港模拟)平行金属板M、N间距离为d。其上有一内壁光滑的半径为R的绝缘圆筒与N板相切,切点处有一小孔S。圆筒内有垂直圆筒截面方向的匀强磁场,磁感应强度为B。电子与孔S及圆心O在同一直线上。M板内侧中点处有一质量为m,电荷量为e的静止电子,经过M、N间电压为U的电场加速后射入圆筒,在圆筒壁上碰撞n次后,恰好沿原路返回到出发点。(不考虑重力,设碰撞过程中无动能损失)求:⑴电子到达小孔S时的速度大小;⑵电子第一次到达S所需要的时间;⑶电子第一次返回出发点所需的时间。
[例2]( 06连云港模拟)平行金属板M、N间距离为d。其上有一内壁光滑的半径为R的绝缘圆筒与N板相切,切点处有一小孔S。圆筒内有垂直圆筒截面方向的匀强磁场,磁感应强度为B。电子与孔S及圆心O在同一直线上。M板内侧中点处有一质量为m,电荷量为e的静止电子,经过M、N间电压为U的电场加速后射入圆筒,在圆筒壁上碰撞n次后,恰好沿原路返回到出发点。(不考虑重力,设碰撞过程中无动能损失)求:⑴电子到达小孔S时的速度大小;⑵电子第一次到达S所需要的时间;⑶电子第一次返回出发点所需的时间。
导示: ⑴设加速后获得的速度为v ,根据 得v=
得v=
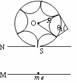 ⑵设电子从M到N所需时间为t1
⑵设电子从M到N所需时间为t1
则 ,得
,得
⑶电子在磁场做圆周运动的周期为
电子在圆筒内经过n次碰撞回到S,每段圆弧对应的圆心角θ1=π-
n次碰撞对应的总圆心角θ=(n+1)θ1=(n+1) π-2π=(n-1) π
在磁场内运动的时间为t2,

 (n=1,2,3,…)
(n=1,2,3,…)


1.直接根据公式 t =s / v 或 t =α/ω求运动时间t;
2.已知入射方向和出射点的位置时,可以通过入射点作入射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂线的交点就是圆弧轨道的圆心。
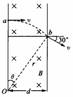 [例1]如图所示,一束电子(电量为e)以速度v垂直射人磁感应强度为B、宽度为d的匀强磁场中,穿过磁场时,速度方向与电子原来的入射方向的夹角是30°,则电子的质量是 ,穿过磁场的时间是
。
[例1]如图所示,一束电子(电量为e)以速度v垂直射人磁感应强度为B、宽度为d的匀强磁场中,穿过磁场时,速度方向与电子原来的入射方向的夹角是30°,则电子的质量是 ,穿过磁场的时间是
。
导示:电子在磁场中只受洛伦兹力作用,(重力忽略)其运动轨迹是圆的一部分。又因为洛伦兹力与速度始终垂直,故圆心在电子穿入a点和穿出b点所受洛伦兹力指向的交点O处,由几何知识可知:ab弧圆心角θ=30°Ob为半径r,

类型二带电粒子在磁场中半径的计算
 利用平面几何关系,求出该圆的可能半径(或圆心角).并注意以下两个重要的几何特点:粒子速度的偏向角(ф)等于回旋角(圆心角α),并等于AB弦与切线的夹角(弦切角θ)的2 倍(如图),即ф=α=2θ=ωt.
利用平面几何关系,求出该圆的可能半径(或圆心角).并注意以下两个重要的几何特点:粒子速度的偏向角(ф)等于回旋角(圆心角α),并等于AB弦与切线的夹角(弦切角θ)的2 倍(如图),即ф=α=2θ=ωt.
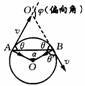
 [例2](06天津卷)在以坐标原点为圆心、半径为r的圆形区域内,存在磁感应强度大小为B、方向垂直于纸面向里的匀强磁场,如图所示。一个不计重力的带电粒子从磁场边界与x轴的交点A处以速度v沿一x方向射入磁场,它恰好从磁场边界与y轴的交点C处沿+y方向飞出。
[例2](06天津卷)在以坐标原点为圆心、半径为r的圆形区域内,存在磁感应强度大小为B、方向垂直于纸面向里的匀强磁场,如图所示。一个不计重力的带电粒子从磁场边界与x轴的交点A处以速度v沿一x方向射入磁场,它恰好从磁场边界与y轴的交点C处沿+y方向飞出。
(1)请判断该粒子带何种电荷,并求出其比荷
(2)若磁场的方向和所在空间范围不变,而磁感应强度的大小变为B′,该粒子仍从A处以相同的速度射入磁场,但飞出磁场时的速度方向相对于入射方向改变了60°角,求磁感应强度B′多大?此次粒子在磁场中运动所用时间是多少?
导示: (1)由粒子的飞行轨迹,利用左手定则可知,该粒予带负电荷。粒子由A点射入,由C点飞出,其速度方向改变了90°,则粒子轨迹
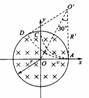

(2)粒子从D点飞出磁场速度方向改变了60°角,故AD弧所对圆心角为60°,粒子做圆周运动的半径

类型三带电粒子在磁场中运动时间
1.已知入射方向和出射方向时,可通过入射点和出射点分别作垂直于入射方向和出射方向的直线,两条直线的交点就是圆弧轨道的圆心.
2.若v⊥B时,带电粒子在垂直于磁感线的平面内以入射速度v做 运动.
结论:①向心力由洛伦兹力提供,即
②轨道半径公式:R= ③周期:T= ④频率:f= 。

知识点一洛伦兹力的方向判断方法
判断洛伦兹力的方向用“左手定则”,在方法上比判断安培力稍复杂一些.这是因为导线中电流的方向(规定为正电荷运动的方向)是惟一明确的.而运动的电荷有正、负电之分,对于运动的正电荷方向就相当于电流的方向;对于运动的负电荷方向相当于与电流相反的方向.
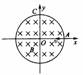
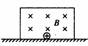 [应用1]有一质量为m,电荷量为q的带正电的小球停在绝缘平面上,并处在磁感应强度为B、方向垂直指向纸面向里的匀强磁场中,如图所示,为了使小球飘离平面,匀强磁场在纸面内移动的最小速度应为多少?方向如何?
[应用1]有一质量为m,电荷量为q的带正电的小球停在绝缘平面上,并处在磁感应强度为B、方向垂直指向纸面向里的匀强磁场中,如图所示,为了使小球飘离平面,匀强磁场在纸面内移动的最小速度应为多少?方向如何?
导示: 小球飘离条件是:mg=Bqv,v=mg/Bq。
由左手定则知:小球应向右运动,也就是磁场要向左运动。
 应审清题目中要求的是匀强磁场的运动,而不是带电小球的运动。
应审清题目中要求的是匀强磁场的运动,而不是带电小球的运动。
知识点二带电粒子的圆周运动
带电粒子以一定的初速度与磁场方向垂直进入匀强磁场时,由于洛伦兹力总是与粒子的运动方向垂直,对粒子不做功,它只改变粒子运动的方向,而不改变粒于的速率,所以粒子受到的洛伦兹力的大小恒定,且F的方向始终与速度垂直,故这个力F充当向心力,因此,只在洛伦兹力作用下,粒予的运动一定是匀速圆周运动.
由有关公式可得出下列关系式:

T、f的两个特点:1. T、f的大小与轨道半径R和运行速率v无关,只与磁感应强度B和粒子的荷质比有关.2.荷质比相同的带电粒于,在同样的匀强磁场中,T、f相同.
[应用2]质子( )和α粒子(
)和α粒子( )从静止开始经相同的电压加速后垂直进入同一匀强磁场做圆周运动,则这两粒子的动能之比凰:Ek1:Ek2=
,轨道半径之比r1: r2= ,周期之比T1:T2= .
)从静止开始经相同的电压加速后垂直进入同一匀强磁场做圆周运动,则这两粒子的动能之比凰:Ek1:Ek2=
,轨道半径之比r1: r2= ,周期之比T1:T2= .
导示: 动能Ek=qU,所以Ek1:Ek2=1:2。半径 ,所以r1: r2=1:
,所以r1: r2=1: 。周期T=2πm/Bq,所以T1:T2=1:2。
。周期T=2πm/Bq,所以T1:T2=1:2。
 作比的方法,在解题中经常用到,使用时应先求出要求的物理量的表达式,然后再求出要求的结果。
作比的方法,在解题中经常用到,使用时应先求出要求的物理量的表达式,然后再求出要求的结果。

类型一带电粒子在磁场中圆心的确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com