
课后记:
比较函数值的大小问题,运用比较法而变成判别代数式的符号。
判断单调性的步骤:设x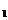 、x
、x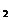 ∈给定区间,且x
∈给定区间,且x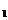 <x
<x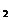 ; →计算f(x
; →计算f(x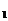 )-f(x
)-f(x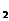 )至最简→判断差的符号→下结论。
)至最简→判断差的符号→下结论。
4.课堂作业:书P32、 2、3、4、5题。
3.讨论f(x)=x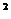 -2x的单调性。 推广:二次函数的单调性
-2x的单调性。 推广:二次函数的单调性
2.判断f(x)=|x|、y=x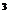 的单调性并证明。
的单调性并证明。
1.求证f(x)=x+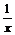 的(0,1)上是减函数,在[1,+∞]上是增函数。
的(0,1)上是减函数,在[1,+∞]上是增函数。
1、 例题讲解
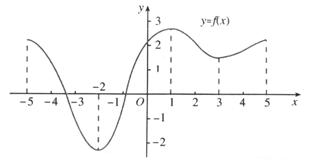
例1(P29例1) 如图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?
例2:(P29例2)物理学中的玻意耳定律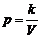 (k为正常数),告诉我们对于一定量的气体,当其体积V增大时,压强p如何变化?试用单调性定义证明.
(k为正常数),告诉我们对于一定量的气体,当其体积V增大时,压强p如何变化?试用单调性定义证明.
例3.判断函数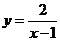 在区间[2,6] 上的单调性
在区间[2,6] 上的单调性
2.教学增函数、减函数的证明:
例1.将进货单价40元的商品按50元一个售出时,能卖出500个,若此商品每个涨价1元,其销售量减少10个,为了赚到最大利润,售价应定为多少?
1.教学增函数、减函数、单调性、单调区间等概念:
①根据f(x)=3x+2、 f(x)=x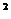 (x>0)的图象进行讨论:
(x>0)的图象进行讨论:
随x的增大,函数值怎样变化? 当x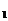 >x
>x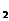 时,f(x
时,f(x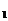 )与f(x
)与f(x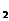 )的大小关系怎样?
)的大小关系怎样?
②.一次函数、二次函数和反比例函数,在什么区间函数有怎样的增大或减小的性质?
③定义增函数:设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说f(x)在区间D上是增函数(increasing function)
④探讨:仿照增函数的定义说出减函数的定义;→ 区间局部性、取值任意性
⑤定义:如果函数f(x)在某个区间D上是增函数或减函数,就说f(x)在这一区间上具有(严格的)单调性,区间D叫f(x)的单调区间。
⑥讨论:图像如何表示单调增、单调减?
所有函数是不是都具有单调性?单调性与单调区间有什么关系?
⑦一次函数、二次函数、反比例函数的单调性
3. 画出函数f(x)= x+2、f(x)= x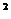 的图像。(小结描点法的步骤:列表→描点→连线)
的图像。(小结描点法的步骤:列表→描点→连线)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com