
78.在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cosB=bcosC.
(1)求角B的大小;
|
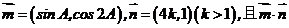 的最大值是5,求k的值.
的最大值是5,求k的值.77.数列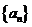 的前
的前 项和为
项和为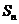 ,
,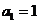 ,
,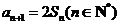 .
.
(1)求数列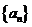 的通项
的通项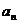 ;(2)求数列
;(2)求数列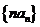 的前
的前 项和
项和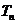 .
.
76.已知A、B、C三点的坐标分别是A(3,0)、B(0,3)、C(cos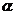 ,sin
,sin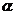 ),其中
),其中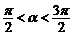 .
.
(1)若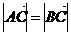 ,求角
,求角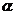 的值;
的值;
(2)若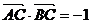 ,求
,求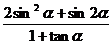 的值.
的值.
75.设函数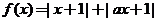 ,已知
,已知 ,且
,且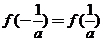 (a∈R,且a≠0),函数
(a∈R,且a≠0),函数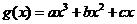 (b∈R,c为正整数)有两个不同的极值点,且该函数图象上取得极值的两点A、B与坐标原点O在同一直线上。
(b∈R,c为正整数)有两个不同的极值点,且该函数图象上取得极值的两点A、B与坐标原点O在同一直线上。
(1)试求a、b的值;(2)若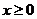 时,函数
时,函数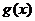 的图象恒在函数
的图象恒在函数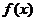 图象的下方,求正整数
图象的下方,求正整数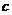 的值。
的值。
74.在锐角三角形ABC中,已知内角A、B、C所对的边分别为a、b、c,
且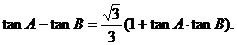
(1)若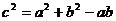 ,求A、B、C的大小;
,求A、B、C的大小;
(2)已知向量 的取值范围.
的取值范围.
73.设函数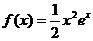 .
.
(1)求f(x)的单调区间;
(2)若当x∈[-2,2]时,不等式f(x)>m恒成立,求实数m的取值范围.
72.已知圆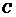 方程为:
方程为: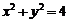 .
.
(1)直线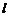 过点
过点 ,且与圆
,且与圆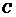 交于
交于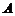 、
、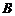 两点,若
两点,若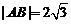 ,求直线
,求直线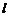 的方程;
的方程;
(2)过圆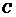 上一动点
上一动点 作平行于
作平行于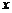 轴的直线
轴的直线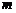 ,设
,设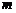 与
与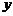 轴的交点为
轴的交点为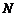 ,若向量
,若向量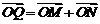 ,求动点
,求动点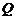 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
71.在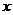 、
、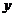 平面上有一系列点
平面上有一系列点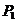 (
(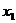 ,
,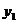 ),
),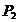 (
(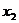 ,
,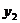 )……
)……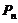 (
(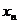 ,
,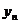 )对每个自然数
)对每个自然数 ,点
,点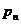 位于函数
位于函数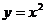 (
(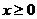 )的图像上,以点
)的图像上,以点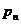 为圆心的圆
为圆心的圆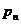 与
与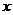 轴相切,且圆
轴相切,且圆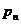 与圆
与圆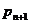 又彼此外切,若
又彼此外切,若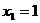 ,且
,且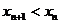 (
(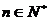 )
)
(1)求证:数列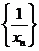 是等差数列;
是等差数列;
(2)设圆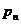 的面积为
的面积为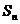 ,
,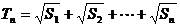 ,求证:
,求证: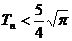 .
.
70.设椭圆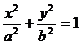
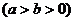 的左焦点为
的左焦点为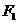
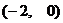 ,左准线
,左准线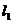 与
与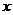 轴交于点N
轴交于点N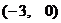 ,过点N且倾斜角为30°的直线
,过点N且倾斜角为30°的直线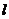 交椭圆于A、B两点.
交椭圆于A、B两点.
(1)求直线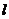 和椭圆的方程;
和椭圆的方程;
(2)求证:点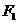
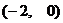 在以线段AB为直径的圆上;
在以线段AB为直径的圆上;
(3)在直线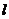 上有两个不重合的动点C、D,以CD为直径且过
上有两个不重合的动点C、D,以CD为直径且过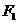 的所有圆中,求面积最小的圆的半径长.
的所有圆中,求面积最小的圆的半径长.
69.已知函数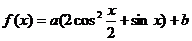
(1)当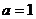 时,求
时,求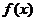 的单调增区间;
的单调增区间;
(2)当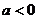 ,且
,且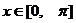 时,
时,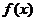 的值域为[
的值域为[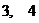 ],求
],求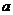 、
、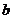 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com