
88、已知在△ABC中,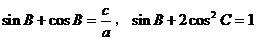 。求角A、B、C的大小。
。求角A、B、C的大小。
87、 在直角坐标平面中,已知点P1(1,2),P2(2,22),……,Pn(n,2n),其中n是正整数,即n∈N*。对平面上任一点A0,记A1为A0关于点P1的对称点,记A2为A1关于点P2的对称点,……,记An为An – 1关于点Pn的对称点。
(1)求向量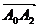 的坐标;
的坐标;
(2)当点A0在曲线C上移动时,点A2的轨迹是函数y = f (x)的图象,其中f (x)是以3为周期的周期函数,且当x∈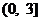 时,f (x)
= lgx;求以曲线C为图象的函数在
时,f (x)
= lgx;求以曲线C为图象的函数在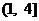 上的解析式;
上的解析式;
(3)对任意偶数n,用n表示向量 的坐标。
的坐标。
86.某厂生产某种零件,每个零件的成本为40元,出厂单价为60元,该厂为鼓励销售订购,决定当一次订购量超过100个时,每多订购1个,订购的全部零件的出厂价格就降低0.02元,但实际出厂单价不能低于51元。
(1)当一次性订购量为多少个时,零件的实际出厂价格恰好为51元。
(2)设一次性订购量为x个,零件的实际出厂单价为p元,写出函数p= f (x)的表达式
(3)当销售商一次订购500个零件时,该厂获得的利润是多少?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂价–成本)
85、设函数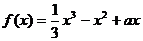 ,
,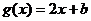 , 当
, 当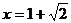 时,
时,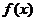 取得极值。
取得极值。
(1)、求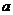 的值,并判断
的值,并判断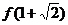 是函数
是函数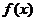 的极大值还是极小值;
的极大值还是极小值;
(2)、当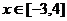 时,函数
时,函数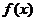 与
与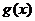 的图象有两个公共点,求
的图象有两个公共点,求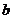 的取值范围.
的取值范围.
84、要建一间地面面积为20m2,墙高为3m的长方体 储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元/ m2,其余三面的造价为200元/ m2,房顶的造价为250元/ m2,问怎样设计储藏室地面矩形的长与宽,能使总造价最低,最低造价是多少?
83.设椭圆C: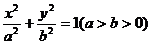 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且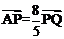 .
.
⑴求椭圆C的离心率;
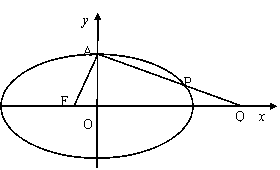 ⑵若过A、Q、F三点的圆恰好与直线l:
⑵若过A、Q、F三点的圆恰好与直线l: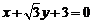 相切,求椭圆C的方程.
相切,求椭圆C的方程.
82.建筑业中,建筑成本费用由城市土地使用权取得费和材料工程费二部分组成。某市今年的土地使用权取得费为2000元/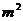 ;材料工程费在建造第一层时为400元/
;材料工程费在建造第一层时为400元/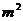 ;以后每增加一层费用增加40元/
;以后每增加一层费用增加40元/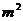 ;求楼高设计为多少层时,才能使平均每平方米建筑面积的成本费最省.
;求楼高设计为多少层时,才能使平均每平方米建筑面积的成本费最省.
81.(本题满分15分)
已知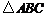 的面积为
的面积为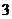 ,且满足
,且满足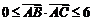 ,设
,设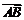 和
和 的夹角为
的夹角为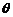 .
.
(1)求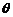 的取值范围;
的取值范围;
(2)求函数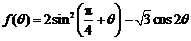 的最大值与最小值.
的最大值与最小值.
80.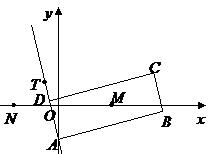 如图,矩形
如图,矩形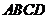 的两条对角线相交于点
的两条对角线相交于点 ,
, 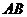 边所在直线的方程为
边所在直线的方程为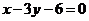 , 点
, 点 在
在 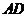 边所在直线上.
边所在直线上.
(1)求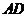 边所在直线的方程;
边所在直线的方程;
(2)求矩形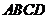 外接圆的方程;
外接圆的方程;
79.已知过点A(0,1),且方向向量为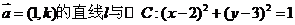 ,相交于M、N两点.
,相交于M、N两点.
(1)求实数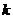 的取值范围;
的取值范围;
(2)求证: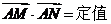 ;
;
(3)若O为坐标原点,且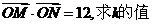 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com