
18、某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求ξ的分布及数学期望;
(Ⅱ)记“函数f(x)=x2-3ξx+1在区间[2,+∞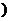 上单调递增”为事件A,求事件A的概率.
上单调递增”为事件A,求事件A的概率.
17、某地最近出台一项机动车驾照考试规定;每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,使可领取驾照,不再参加以后的考试,否则就一直考到第4次为止。如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年内李明参加驾照考试次数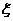 的分布列和
的分布列和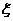 的期望,并求李明在一年内领到驾照的概率.
的期望,并求李明在一年内领到驾照的概率.
16、甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,所出次品数分别为ξ 、η,且ξ和η的分布列为:
|
ξ |
0 |
1 |
2 |
|
P |
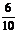 |
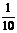 |
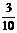 |
试比较这两名工人谁的技术水平更高.
15、从4名男生和2名女生中任选3人参加演讲比赛,设随机变量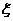 表示所选3人中女生的人数.
表示所选3人中女生的人数.
(Ⅰ)求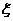 的分布列;
的分布列;
(Ⅱ)求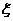 的数学期望;
的数学期望;
(Ⅲ)求“所选3人中女生人数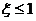 ”的概率.
”的概率.
|
η |
0 |
1 |
2 |
|
P |
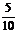 |
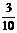 |
 |
14、某公司有5万元资金用于投资开发项目,如果成功,一年后可获利12%,一旦失败,一年后将丧失全部资金的50%,下表是过去200例类似项目开发的实施结果:
|
投资成功 |
投资失败 |
|
192次 |
8次 |
则该公司一年后估计可获收益的期望是___________(元)..
13、一个容量为n的样本,分成若干组,已知某组频数和频率分别为36和0.25,则n=__________.
12、一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出2个球,则其中含红球个数的数学期望是 .
11、随机变量ξ的分布列为P(ξ=k)=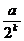 (k=0,1,2,…,10)则
(k=0,1,2,…,10)则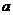 =
.
=
.
10、如果随机变量ξ-N (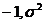 ),且P(
),且P(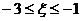 )=0.4,则P(
)=0.4,则P(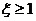 )
)
等于 ( )
A. 0.1 B. 0.2 C. 0.3 D. 0.4
9、如果随机变量ξ-N (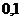 ),标准正态分布表中相应
),标准正态分布表中相应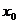 的值为
的值为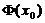 则 (
)
则 (
)
A.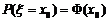 B.
B.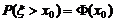
C.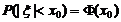 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com