
6.下面这首小诗在对“树”进行描写时涉及了作者对“岁月”的思考,请选择另外两种事
物,仿照例句的表达方式和句式,各写一句话,描述事物必须涉及对“生命”的思考。
(4分)
树:如果你挺直了你的身躯,风会比你矮很多,伟岸就会溢满你的岁月
(1) 。
(2) 。
5.下列各句正确的排列顺序是: 。(只填序号)(3分)
①他先把一只黑色的钟漏放在刑台上的一角
②他用左手随便地把衬衣的右边那只袖子卷起来,一直卷到腋下
③人们看见他右胳膊上挂着一条用许多长长的、闪光的、紧扎的、尖端包着金属的白皮
条扎成的鞭子
④那钟漏的上一层装满红色的沙子,沙子不断地向下面一层漏去
⑤随后他便脱掉他那两色的外衣
4.下列各句没有语病的一项是
A.只要我们坚持对话,摈弃偏见,增进交流,消除隔阂,人类文化一定会展现出共同
繁荣、异彩纷呈的灿烂前景。
B.古往今来,仁人志士们以雄才大略行富国强民之道,民主之梦,经世济民的卓越思
想和心忧天下的高尚情怀代代传承。
C.人类社会始终存在希望,是由于每当黑暗笼罩时,总有思想的先驱掏出燃烧的心举
过头顶,拆下肋骨当火把,照亮前行的路的缘故。
D.作为现代公民的重要素养,口语交际能力显示着一个人的自信与智慧、教养与风度,
更体现着一个人的语言水平。
3.下列加点熟语使用不正确的一项是
A.对于不骄傲的、不采取盛气凌人的“西方态度”并知道自己最高思想来自东方的、
无愧于自己的理想的科学家来说,将是一个更高尚的人。
B.自鸦片战争以来,我们不少人认为,不仅在科学上要向西方学习,在艺术上也要向
西方靠拢,结果就像邯郸学步一样,别人的东西没学好,自己的传统反而被遗忘了。
C.理科生说我在国际上拿了金牌回来了,这个金牌是无可厚非的。问题是文学就很难
量化呀。
D.从不主张拆除城墙的人的论点上说,这种看法是有偏见的,由全面城市计划的观点
看来,都是只知其一不知其二的,见树不见林的。
2.下列各句没有错别字的一项是
A.这幢清寒的小屋,远离通渠大道。荦荦孑立于田野之间,隐蔽在花园的密林深处。
B.青少年往往为陈旧、复杂的教学方法,愚蠢和严厉相交替的说教以及拙劣肤浅的哲
学所束缚而失去平衡。
C.事实上,很多老年人虽然还没有听说过“精神瞻养”这个词,但生活中他们对精神
瞻养的须求却是明确而实在的。
D.只要有人,只要有生活,人性就会演义出多采的故事,而真与假,美与丑,善与恶,
则是它反复呈现的主题。
1.下列加点字读音全对的一项是
A.铿锵(jiāng) 婉转(wǎn) 沁人(qìn) 抛锚(máo) 庇护(pì)
B.灰烬(jǐn) 狐裘(qiú) 颓垣(yuán) 荒冢(zǒng) 罡风(gāng)
C.轮轴(zhóu) 哄笑(hōng) 瞭望(1iào) 褶皱(zhě) 伛曲(yǔ)
D.繁芜(wú) 邮戳(jié) 缄口(jiān) 汗涔涔(chén) 旌旗(jīng)
9.(2006全国I)如图,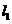 、
、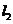 是互相垂直的异面直线,MN是它们的公垂线段
是互相垂直的异面直线,MN是它们的公垂线段 点A、B在
点A、B在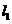 上,C在
上,C在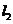 上,
上,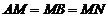

(Ⅰ)证明 ⊥
⊥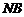 ;
;
(Ⅱ)若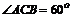 ,求
,求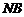 与平面ABC所成角的余弦值
与平面ABC所成角的余弦值
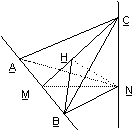

证明 (Ⅰ)由已知l2⊥MN, l2⊥l1 , MN∩l1 =M, 可得l2⊥平面ABN 由已知MN⊥l1 , AM=MB=MN,可知AN=NB且AN⊥NB
由已知MN⊥l1 , AM=MB=MN,可知AN=NB且AN⊥NB
又AN为AC在平面ABN内的射影 ∴AC⊥NB
∴AC⊥NB
(Ⅱ)∵Rt△CAN≌Rt△CNB,
∴AC=BC,又已知∠ACB=600,
因此△ABC为正三角形.
∵Rt△ANB≌Rt△CNB,
∴NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心,连结BH,∠NBH为NB与平面ABC所成的角 在Rt△NHB中,
在Rt△NHB中,
cos∠NBH= = = 
[探索题]
如图,在600的二面角α-CD-β中,AC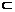 α,BD
α,BD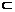 β,且ACD=450,tg∠BDC=2,CD=a,AC=
β,且ACD=450,tg∠BDC=2,CD=a,AC=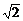 x,BD=
x,BD=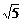 x,当x为何值时,A、B的距离最小?并求此距离.
x,当x为何值时,A、B的距离最小?并求此距离.
解析:
作AE⊥CD于E,BF⊥CD于F,则EF为异面直线AE、BF的公垂段,AE与BF成600角,可求得|AB|=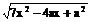 ,当x=
,当x=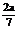 时,|AB|有最小值
时,|AB|有最小值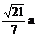 .
.
8. (2004广东)如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2。E、F分别是线段AB、BC上的点,且EB=BF=1。求直线EC1与FD1所成的角的余弦值。
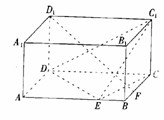
解:延长BA至点E1,使AE1=1,连结E1F、DE1、D1E1、DF,有 D1C1//E1E, D1C1=E1E,则四边形D1E1EC1是平行四边形。则E1D1//EC1.于是∠E1D1F为直线
D1C1//E1E, D1C1=E1E,则四边形D1E1EC1是平行四边形。则E1D1//EC1.于是∠E1D1F为直线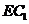 与
与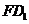 所成的角。
所成的角。
在Rt△BE1F中,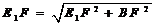 .
.
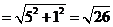 . 在Rt△D1DE1中,
. 在Rt△D1DE1中, 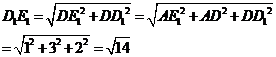
在Rt△D1DF中,
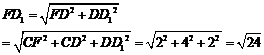
在△E1FD1中,由余弦定理得:
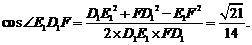
∴直线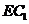 与
与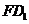 所成的角的余弦值为
所成的角的余弦值为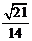 .
.
7.已知正方体ABCD-A1B1C1D1的边长为a,E、F分别是棱A1B1、CD的中点.
(1)证明:截面C1EAF⊥平面ABC1.
(2)求点B到截面C1EAF的距离.
证明(1):连结EF、AC1和BC1,易知四边形EB1CF是平行四边形,从而EF∥B1C,直线B1C⊥BC1且B1C⊥AB,则直线B1C⊥平面ABC1,得EF⊥平面ABC1.而EF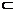 平面C1EAF,得平面C1EAF⊥平面ABC1.
平面C1EAF,得平面C1EAF⊥平面ABC1.
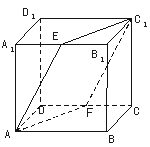

解(2):在平面ABC1内,过B作BH,使BH⊥AC1,H为垂足,则BH的长就是点B到平面C1EAF的距离,在直角三角形中,BH=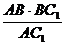 =
=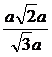 =
=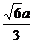 .
.
6.已知l1、l2是两条异面直线,α、β、γ是三个平面依次互相平行,l1、l2分别交α、β、γ于A、B、C和D、E、F,AB=4,BC=12,DF=10,又l1与α成30°角,则β与γ的距离是__________;DE=__________.
◆答案: 1-4.DAAB;
5.  ; 6. 6 、 2.5;
; 6. 6 、 2.5;
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com