
1. (2008安徽卷,理,14)在数列 在中,
在中, ,
,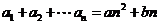 ,
,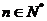 ,其中
,其中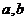 为常数,则
为常数,则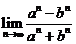 的值是 .
的值是 .
[解析]本题根据通项与前n项和可以求出常数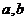 的值,再对所给的有限项求极限.这里我们要利用已经掌握的无限的结论(即
的值,再对所给的有限项求极限.这里我们要利用已经掌握的无限的结论(即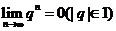 )来解决新的极限问题.
)来解决新的极限问题.
[答案]由 知,
知, 是公差为4的等差数列,故
是公差为4的等差数列,故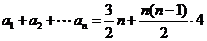
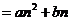 ,解得
,解得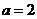 ,
,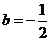 ,从而
,从而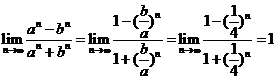 .
.
5、有限与无限的思想在近几年的高考中已经有很多具体的体现,随着高中课程改革,对新增内容的深入考查,必将加大对这一思想的考查,所以我们考前应该予以重视.
4、立体几何中求球的表面积与体积的推导,实际上是先进行有限次分割,然后再求和、求
极限;数学归纳法就是通过对有限的研究来解决无限的问题等等,这些都是典型的有限与无限思想的应用.取极限和数学归纳法就是由有限与无限的思想得到的具体的方法.
3、积累的解决无限问题的经验,将有限问题转化为无限问题来解决是解决有限问题的一个方向,同时有利于解决新的无限的问题.
2、把对无限的研究转化为对有限的研究,是解决无限问题的必经之路.
1、有限与无限的思想就是将无限的问题化为有限来求解,将有限的问题化为无限来解决,利用已经掌握的无限问题的结论来解决新的无限问题.
7. 预测题
预测题
(1)(2008宁夏银川一中,改编)已知函数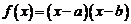 (其中
(其中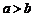 ),
),


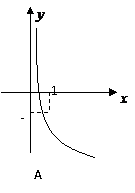 若
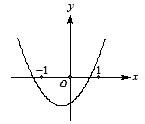
若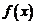 的图像如右图所示,则函数
的图像如右图所示,则函数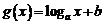 的图像是( )
的图像是( )

分析:由已知二次函数解析式及二次函数的图象可以判断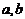 的取值范围,从而判断
的取值范围,从而判断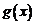 的图象.
的图象.
解: 由函数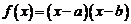 (其中
(其中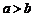 )的图象可知,
)的图象可知,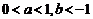 .把
.把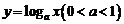 的图象向下平移
的图象向下平移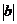 个单位,故选A.
个单位,故选A.
答案:A
评注:学会识图,读图,画图,并进行图象的平移变换.
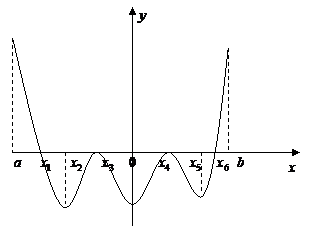 (2)(2008山东省聊城市,改编)函数
(2)(2008山东省聊城市,改编)函数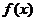 的定义域为(a,b),其导函数
的定义域为(a,b),其导函数
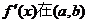 内的图象如图所示,则函
内的图象如图所示,则函
数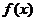 在区间(a,b)内极值点的个数是 ( )
在区间(a,b)内极值点的个数是 ( )
A.1 B.2 C.3 D. 4
分析:要判断函数的极值点,要先找导函数的零点,再看此点
两侧的导函数的符号,如果异号就是原函数的极值点.
解:由导函数图知, 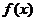 只在
只在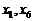 处的导数值为0,且两侧的符号相异.
处的导数值为0,且两侧的符号相异.
函数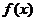 在区间(a,b)内极值点的个数为2个
在区间(a,b)内极值点的个数为2个
评注:判断函数的极值点不能只找导函数的零点,还要看此零点两侧的导函数的符号,如果异号就是原函数的极值点.本题图中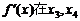 处虽然也为零,但因其两侧的符号相同,而不是函数
处虽然也为零,但因其两侧的符号相同,而不是函数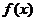 在区间(a,b)内极值点.
在区间(a,b)内极值点.
(3)(原创)设实数x, y满足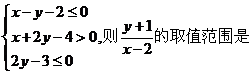
 分析: 作出不等式表示的可行域,再画出可行域内的点与点
分析: 作出不等式表示的可行域,再画出可行域内的点与点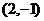 连线,数形结合解答.
连线,数形结合解答.
解: 作出不等式表示的可行域如图所示,
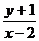 表示可行域内的点与点
表示可行域内的点与点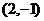 连线的斜率,
连线的斜率,
则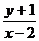 的取值范围是
的取值范围是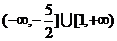
答案: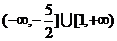
评注:作出不等式表示的可行域后, 在画出可行域内的点与
点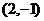 连线时,要画准确,其中有一条直线的斜率不存在,
连线时,要画准确,其中有一条直线的斜率不存在,
注意斜率的取值范围应该为两直线对应的斜率之外.
(4)(08山东卷,理12改编)设二元一次不等式组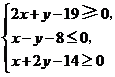 所表示的平面区域为
所表示的平面区域为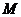 ,使函数
,使函数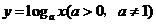 的图象过区域
的图象过区域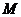 的
的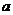 的取值范围是( )
的取值范围是( )
A.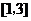 B.
B.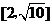 C.
C.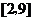 D.
D.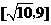
分析:先画出不等式表示的平面区域,再画出对数函数的图象,借助图形解答。
 解:
区域
解:
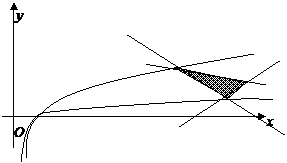
区域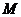 是一个三角形区域,三个顶
是一个三角形区域,三个顶
点的坐标是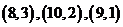 ,结合图
,结合图
形检验可知当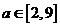 时,符合题目要求。
时,符合题目要求。
评注:解决不等式表示的平面区域和
函数问题都要用数形结合,做到一目了然。
(5)(2008海南卷,理11,改编)已知点P在抛物线 上,那么点P到点
上,那么点P到点 的距离与点P到
的距离与点P到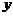 轴的距离之和取得最小值时,点P的坐标为( )
轴的距离之和取得最小值时,点P的坐标为( )
A. B.
B.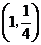 C.
C.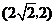 D.
D.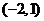
分析: 点P到点 的距离与点P到
的距离与点P到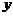 轴的距离之和取得最小值时, 点P到点
轴的距离之和取得最小值时, 点P到点 的距离与点P到抛物线的准线的距离之和也取得最小值,这样就可以把点P到抛物线的准线的距离转为到焦点的距离求出.
的距离与点P到抛物线的准线的距离之和也取得最小值,这样就可以把点P到抛物线的准线的距离转为到焦点的距离求出.
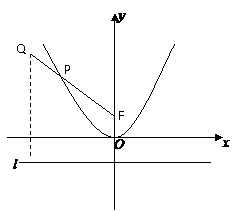 解: 点
解: 点 在抛物线
在抛物线 的外部,要使点P到点
的外部,要使点P到点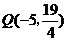 的距离与点P到
的距离与点P到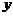 轴的距离之和取得最小值,根据抛物线的定义知,须使点P到点
轴的距离之和取得最小值,根据抛物线的定义知,须使点P到点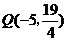 的距离与点P到抛物线焦点距离之和取得最小,即
的距离与点P到抛物线焦点距离之和取得最小,即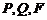 三点共线时最小. 由斜率
三点共线时最小. 由斜率
公式得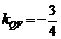 ,所以
,所以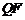 的方程为
的方程为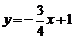 ,
,
解方程组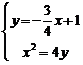 得,点
得,点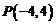 ,故选A.
,故选A.
答案:A
评注:抛物线的定义是到焦点的距离等于到准线的距离,
做题时常常用定义进行转化.
(6)、已知函数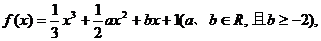 当
当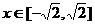 时,总有
时,总有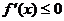 .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设函数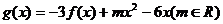 ,求证:当
,求证:当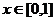 时,
时,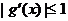 的充要条件是
的充要条件是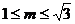 .
.
分析:三次函数的导函数为二次函数,那么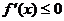 为二次不等式,当
为二次不等式,当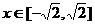 时,总有
时,总有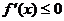 .就要结合二次函数的图象进行转化;当
.就要结合二次函数的图象进行转化;当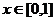 时,
时,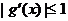 成立也是二次不等式恒成立问题也要结合着二次函数的图象完成。
成立也是二次不等式恒成立问题也要结合着二次函数的图象完成。
解:(Ⅰ)由条件,得 ,
,
当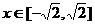 时,总有
时,总有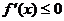 ,所以有
,所以有
|
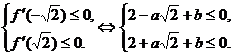
由①+②得,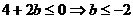 ,
,
又b≥-2,∴b=-2,把b=-2代入①和②得
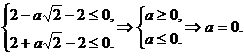
因此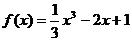 .
.
(Ⅱ) ,
,
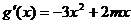 是关于x的二次函数,
是关于x的二次函数,
当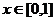 时,
时, 或
或
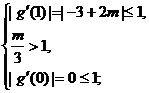 或
或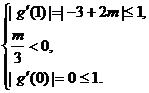
解得,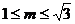 . 因此,当
. 因此,当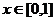 时,
时,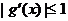 的充要条件是
的充要条件是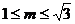
评注:二次函数,二次方程,二次不等式问题常常要结合着二次函数的图象来完成,对于二次不等式来说一般要从二次抛物线的开口方向,对称轴,判别式和端点对应的函数值四方面来解答。

6.解析几何问题常常数形结合
例10.(2008海南卷,理11)已知点P在抛物线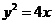 上,那么点P到点
上,那么点P到点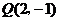 的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
 A.
A.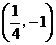 B.
B.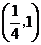 C.
C.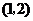 D.
D.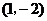
分析: 点P到点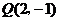 的距离与点P到抛物线焦点的距离之和取得最小值时, 点P到点
的距离与点P到抛物线焦点的距离之和取得最小值时, 点P到点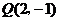 的距离与点P到抛物线的准线的距离之和也取得最小值,这样就可以把点P到抛物线的焦点的距离转为到准线的距离求出.
的距离与点P到抛物线的准线的距离之和也取得最小值,这样就可以把点P到抛物线的焦点的距离转为到准线的距离求出.
解: 点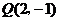 在抛物线
在抛物线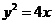 的内部,要使点P到点
的内部,要使点P到点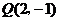 的
的
 距离与点P到抛物线焦点的距离之和取得最小值,根据抛物线的
距离与点P到抛物线焦点的距离之和取得最小值,根据抛物线的
定义知,须使点P到点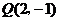 的距离与点P到抛物线准线
的距离与点P到抛物线准线
距离之和取得最小,即 时最小.则
时最小.则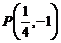 故选A.
故选A.
答案:A
评注:抛物线的定义是到焦点的距离等于到准线的距离,做题时常常用定义进行转化.
例11.(福建德化一中2008,理)已知函数f(x)= , 若0<x1<x2<1, 则 ( )
A. > B. = C. < D. 前三个判断都不正确
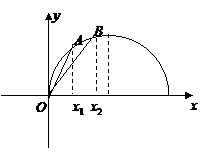
分析:从解析式上看函数与圆的方程有联系,可以转化为圆,画出图形,由数形结合得出结论。
 解:由函数
解:由函数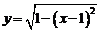 得
得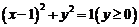 知
知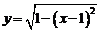 的图象为圆
的图象为圆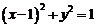 的上半圆,如图,当0<x1<x2<1时,和分别
的上半圆,如图,当0<x1<x2<1时,和分别
为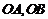 的斜率,由图可知
的斜率,由图可知 ,∴ > ,故选A
,∴ > ,故选A
评注:对于函数的图象要熟悉,利用数形结合解答函数的选择题
比较形象直观,容易找到关系。
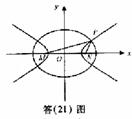
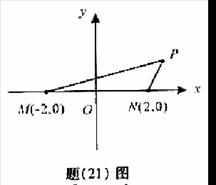 例12.(2008重庆卷,理21)如图(21)图,M(-2,0)和N(2,0)是平面上的两点,动点P满足:
例12.(2008重庆卷,理21)如图(21)图,M(-2,0)和N(2,0)是平面上的两点,动点P满足: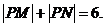
(Ⅰ)求点P的轨迹方程;
(Ⅱ)若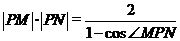 ,求点P的坐标.
,求点P的坐标.
分析:根据已知条件和椭圆的定义易得点P的轨迹方程,
由(2)中的等式可变形转为向量的模和数量积,结合总条件,
在三角形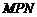 中研究边与角之间的关系。
中研究边与角之间的关系。
解:(Ⅰ)由椭圆的定义,点P的轨迹是以M、N为焦点,长轴长2a=6的椭圆.
 因此半焦距c=2,长半轴a=3,从而短半轴,b=
因此半焦距c=2,长半轴a=3,从而短半轴,b=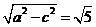 ,
,
所以椭圆的方程为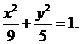
(Ⅱ)由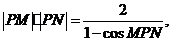 得
得
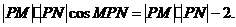 ①
①
 因为
因为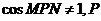 不为椭圆长轴顶点,故P、M、N构成三角形.在△PMN中,
不为椭圆长轴顶点,故P、M、N构成三角形.在△PMN中,
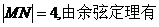
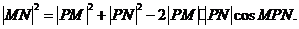 ②
②
将①代入②,得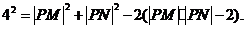 故点P在以M、N为焦点,实轴长为
故点P在以M、N为焦点,实轴长为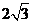 的双曲线
的双曲线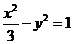 上. 由(Ⅰ)知,点P的坐标又满足
上. 由(Ⅰ)知,点P的坐标又满足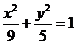 ,所以由方程组
,所以由方程组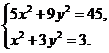 解得
解得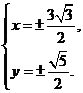 即P点坐标为
即P点坐标为
评注:解析几何问题要画出图形,采用数形结合的方法解答。
5.利用函数借助图形求面积
例9.(2008山东省聊城市
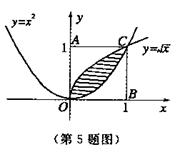 ).曲线
).曲线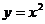 和
和
曲线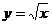 围成一个叶形图(如图所示阴影部分),
围成一个叶形图(如图所示阴影部分),
其面积是 ( )
A.1 B.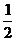 C.
C.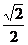 D.
D.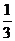
分析: 两条曲线围成的面积用微积分求出,并且是上面的函数减去下面的函数的积分.
解:两条曲线的交点为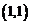 ,阴影部分的面积为
,阴影部分的面积为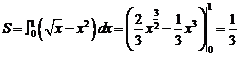
评注:对于曲线所围成的不规则的几何图形的面积,要用微积分解答,注意积分的上限和下限,有时要看图形是否需要切分成多块部分求出.
4.利用不等式表示的平面区域解答问题
例7.(2008年安徽卷,理15)若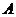 为不等式组
为不等式组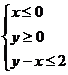 表示的平面区域,
表示的平面区域,
则当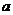 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线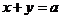 扫过
扫过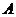 中的那部分区域的面积为
中的那部分区域的面积为
分析:作出不等式表示的平面区域,然后再作平行线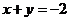 和
和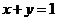
则夹在两平行线之间的部分即为所求。
解:如图知 是斜边为3 的等腰直角三角形,
是斜边为3 的等腰直角三角形, 是直
是直
角边为1等腰直角三角形,区域的面积
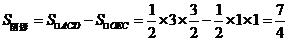
评注:涉及到不等式表示的平面区域问题时常常要画出图形数形结合解答问题。
例8.(2008年浙江,理17)若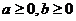 ,且当
,且当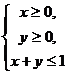 时,恒有
时,恒有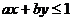 ,则以
,则以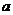 ,b为坐标点P(
,b为坐标点P(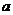 ,b)所形成的平面区域的面积等于__________。
,b)所形成的平面区域的面积等于__________。
 分析:本小题主要考查线性规划的相关知识,可考虑特殊情形,
分析:本小题主要考查线性规划的相关知识,可考虑特殊情形,
比如x=0,可得a=1;y=0可得b=1.所以猜测a介于0和1之间,
b介于0和1之间。
解:不等式组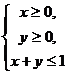 表示的平面区域为
表示的平面区域为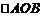 ,如图,
,如图,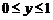
由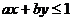 恒成立知,当
恒成立知,当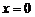 时,
时,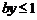 恒成立,当
恒成立,当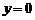 成立;当
成立;当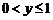 时,
时,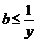 恒成立,∴
恒成立,∴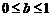 ;同理,
;同理,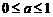 ∴以
∴以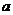 ,b为坐标点P(
,b为坐标点P(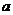 ,b)所形成的平面区域是一个正方形,所以面积为1。
,b)所形成的平面区域是一个正方形,所以面积为1。
答案:1
评注:线性规划的相关知识要画出图形,借助图形解答。另外对于恒成立问题,对个例一定成立,还要转为函数的最值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com