
4.周期函数的定义:对于函数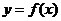 ,如果存在一个不等于
,如果存在一个不等于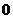 的常数
的常数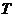 ,使得当
,使得当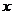 取定义域内的任意值时都有
取定义域内的任意值时都有 ,则
,则 是周期函数,
是周期函数,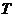 是它的一个周期.对于一个周期函数,如果所有周期中存在一个最小的正的周期,就把这个周期叫做最小正周期.
是它的一个周期.对于一个周期函数,如果所有周期中存在一个最小的正的周期,就把这个周期叫做最小正周期.
教材透析
知识点1:奇偶函数的定义域关于原点对称,解题时要优先考虑;定义域不关于原点对称的函数一定是非奇非偶函数.
知识点2:函数奇偶性的判断方法:①定义域关于原点对称;②对于奇函数若定义域中有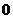 ,则
,则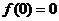 ;③ 特值检验,然后再证明;④利用某些性质:在公共定义域内,偶函数与偶函数的和(或差或积或商)是偶函数,奇函数与奇函数的和(或差或积或商)是奇函数,(作商时,注意分母不能为
;③ 特值检验,然后再证明;④利用某些性质:在公共定义域内,偶函数与偶函数的和(或差或积或商)是偶函数,奇函数与奇函数的和(或差或积或商)是奇函数,(作商时,注意分母不能为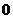 )奇函数与偶函数的积与商为奇函数.
)奇函数与偶函数的积与商为奇函数.
知识点3:函数奇偶性的应用①作函数图像;②求解析式;③奇偶性与单调性的联系:奇函数的对称区间上单调性相同,偶函数的对称区间上单调性相反;④利用奇偶性求值.
知识点4:若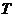 是函数的周期,则
是函数的周期,则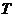 的整数倍也是函数的周期.
的整数倍也是函数的周期.
典例剖析
[题型1]判断函数的周期性
[例1](2002全国文)设函数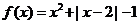 ,
, .
.
(1)判断函数 的奇偶性;
的奇偶性;
(2)求函数 的最小值.
的最小值.
[解析](1)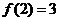 ,
,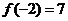
由于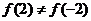 ,
,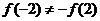
故 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(2)f(x)=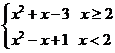 ,
,
由于 在
在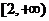 上的最小值为
上的最小值为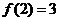 ,在
,在 内的最小值为
内的最小值为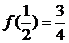 ,
,
故函数 在
在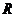 内的最小值为
内的最小值为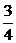 .
.
[点评]因为奇偶函数问题要紧紧抓住“任取”“都有”这两个关键词.  与
与 要同时有意义,f(x)与f(-x)要么相等,要么互为相反数,而要讨论非奇非偶只要说明不满足上述两点之一即可.另外,也可以借助分段函数的草图,帮助分析,然后用代数方法来回答.
要同时有意义,f(x)与f(-x)要么相等,要么互为相反数,而要讨论非奇非偶只要说明不满足上述两点之一即可.另外,也可以借助分段函数的草图,帮助分析,然后用代数方法来回答.
[变式与拓展]
3.奇、偶函数的性质
(1)具有奇偶性的函数,其定义域关于原点对称(也就是说,函数为奇函数或偶函数的必要条件是其定义域关于原点对称).
(2)奇函数的图象关于原点对称,偶函数的图象关于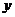 轴对称.
轴对称.
(3)若奇函数的定义域包含数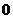 ,则
,则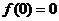 .
.
(4)奇函数的反函数也为奇函数.
(5)定义在(-∞,+∞)上的任意函数f(x)都可以唯一表示成一个奇函数与一个偶函数之和.
2.偶函数:对于函数.的定义域内任意一个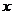 ,都有
,都有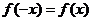
(或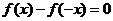 ),则称
),则称 为偶函数.
为偶函数.
1.奇函数:对于函数 的定义域内任意一个
的定义域内任意一个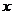 ,都有
,都有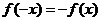
(或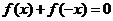 ),则称
),则称 为奇函数.
为奇函数.
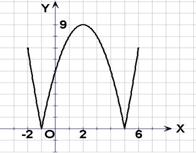
12.(2006年上海春)设函数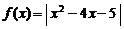 .
.
(1)在区间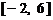 上画出函数
上画出函数 的图像;
的图像;
(2)设集合
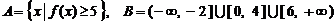 ,
,
试判断集合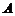 和
和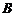 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当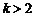 时,求证:在区间
时,求证:在区间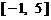 上,
上, 的图像位于函数
的图像位于函数 图像的上方.
图像的上方.
解:(1)如图所示:
(2)方程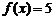 的解分别是
的解分别是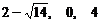 和
和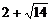 ,由于
,由于 在
在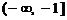 和
和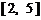 上单调递减,在
上单调递减,在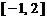 和
和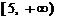 上单调递增,因此
上单调递增,因此
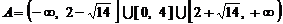 .
.
由于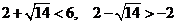 ,∴
,∴ .
.
(3)[解法一] 当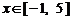 时,
时,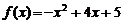 .
.
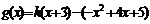
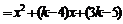
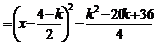 ,
,
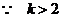 ,∴
,∴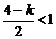 ,又
,又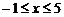 ,
,
① 当 ,即
,即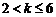 时,取
时,取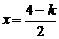 ,
,
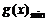
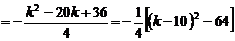 .
.
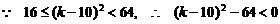 , 则
, 则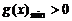 .
.
② 当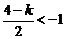 ,即
,即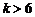 时,取
时,取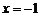 ,
, 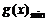 =
=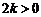 .
.
由 ①、②可知,当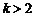 时,
时,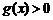 ,
,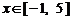 .
.
因此,在区间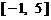 上,
上,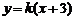 的图像位于函数
的图像位于函数 图像的上方.
图像的上方.
[解法二] 当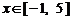 时,
时,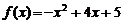 .
.
由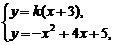 得
得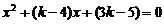 ,
,
令 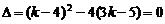 ,解得
,解得
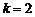 或
或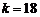 ,
,
在区间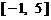 上,当
上,当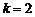 时,
时,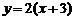 的图像与函数
的图像与函数 的图像只交于一点
的图像只交于一点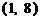 ;
当
;
当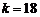 时,
时,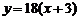 的图像与函数
的图像与函数 的图像没有交点.
的图像没有交点.
如图可知,由于直线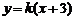 过点
过点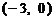 ,当
,当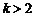 时,直线
时,直线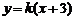 是由直线
是由直线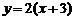 绕点
绕点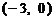 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间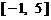 上,
上,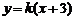 的图像位于函数
的图像位于函数 图像的上方.
图像的上方.
第三节 函数的奇偶性和周期性
自主学习
11.(2007湖北文)设二次函数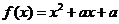 ,方程
,方程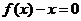 的两根
的两根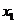 和
和 满足
满足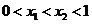 .
.
(1)求实数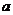 的取值范围;
的取值范围;
(2)试比较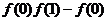 与
与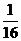 的大小,并说明理由.
的大小,并说明理由.
[解析](1)令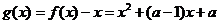 ,
,
则由题意可得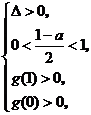
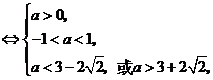
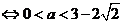 .
.
故所求实数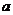 的取值范围是
的取值范围是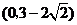 .
.
(2)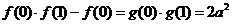 ,令
,令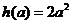 .
.
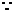 当
当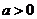 时,
时,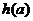 单调增加,
单调增加,
∴当 时,
时,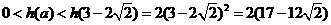
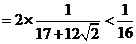 ,即
,即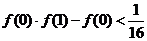 .
.
10.设f(x)、g(x)都是单调函数,有如下四个命题:
①若f(x)单调递增,g(x)单调递增,则f(x)-g(x)单调递增;
②若f(x)单调递增,g(x)单调递减,则f(x)-g(x)单调递增;
③若f(x)单调递减,g(x)单调递增,则f(x)-g(x)单调递减;
④若f(x)单调递减,g(x)单调递减,则f(x)-g(x)单调递减.
其中,正确的命题是 ② ③ .
三 解答题
9. 如果函数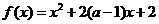 在区间
在区间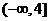 上是减函数,那么实数a的取值范围是
上是减函数,那么实数a的取值范围是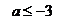 .
.
8.函数y=loga(2-ax)在[0,1]上是减函数,则a的取值范围是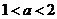 .
.
7.(2006年湖北省荆州市高中毕业班质量检查题)函数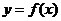 的图象与
的图象与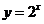 的图象关于直线
的图象关于直线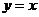 对称,则函数
对称,则函数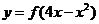 的递增区间是
的递增区间是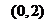 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com