
1.(08山东)不等式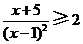 的解集是( )
的解集是( )
A.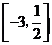 B.
B.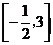 C.
C.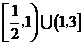 D.
D.
例1设函数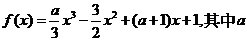 为实数。
为实数。
(Ⅰ)已知函数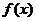 在
在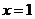 处取得极值,求
处取得极值,求 的值;
的值;
(Ⅱ)已知不等式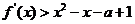 对任意
对任意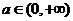 都成立,求实数
都成立,求实数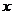 的取值范围。
的取值范围。
解: (1) 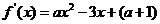 ,由于函数
,由于函数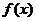 在
在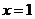 时取得极值,所以
时取得极值,所以 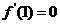
即 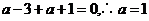
(2)由题设知: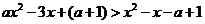 对任意
对任意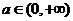 都成立
都成立
即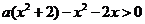 对任意
对任意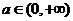 都成立
都成立
于是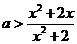 对任意
对任意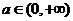 都成立,即
都成立,即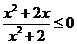
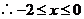
于是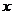 的取值范围是
的取值范围是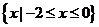
例2.解关于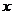 的不等式:
的不等式: 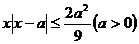
分析:本例主要复习含绝对值不等式的解法,分类讨论的思想。本题的关键不是对参数 进行讨论,而是去绝对值时必须对末知数进行讨论,得到两个不等式组,最后对两个不等式组的解集求并集,得出原不等式的解集。
进行讨论,而是去绝对值时必须对末知数进行讨论,得到两个不等式组,最后对两个不等式组的解集求并集,得出原不等式的解集。
解:当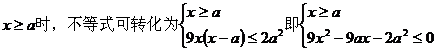
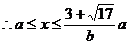
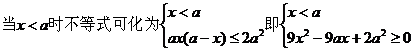
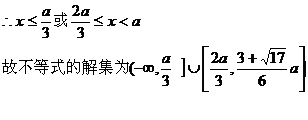 。
。
例3. 己知三个不等式:①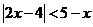
 ②
②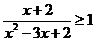 ③
③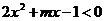
(1)若同时满足①、②的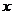 值也满足③,求m的取值范围;
值也满足③,求m的取值范围;
(2)若满足的③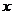 值至少满足①和②中的一个,求m的取值范围。
值至少满足①和②中的一个,求m的取值范围。
分析:本例主要综合复习整式、分式不等式和含绝对值不等的解法,以及数形结合思想,解本题的关键弄清同时满足①、②的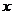 值的满足③的充要条件是:③对应的方程的两根分别在
值的满足③的充要条件是:③对应的方程的两根分别在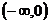 和
和 内。不等式和与之对应的方程及函数图象有着密不可分的内在联系,在解决问题的过程中,要适时地联系它们之间的内在关系。
内。不等式和与之对应的方程及函数图象有着密不可分的内在联系,在解决问题的过程中,要适时地联系它们之间的内在关系。
解:记①的解集为A,②的解集为B,③的解集为C。
解①得A=(-1,3);解②得B=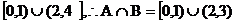
(1)
因同时满足①、②的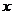 值也满足③,A
值也满足③,A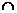 B
B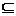 C
C
设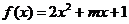 ,由
,由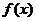 的图象可知:方程的小根小于0,大根大于或等于3时,即可满足
的图象可知:方程的小根小于0,大根大于或等于3时,即可满足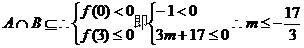
(2)
因满足③的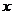 值至少满足①和②中的一个,
值至少满足①和②中的一个,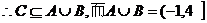 因
因
此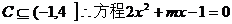 小根大于或等于-1,大根小于或等于4,因而
小根大于或等于-1,大根小于或等于4,因而

例4.若二次函数y=f(x)的图象经过原点,且1≤f(-1)≤2,3≤f(1)≤4,求f(-2)的范围.
分析:要求f(-2)的取值范围,只需找到含人f(-2)的不等式(组).由于y=f(x)是二次函数,所以应先将f(x)的表达形式写出来.即可求得f(-2)的表达式,然后依题设条件列出含有f(-2)的不等式(组),即可求解.
解:因为y=f(x)的图象经过原点,所以可设y=f(x)=ax2+bx.于是
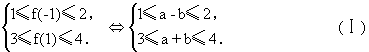
解法一(利用基本不等式的性质)
不等式组(Ⅰ)变形得
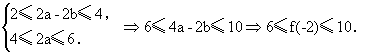
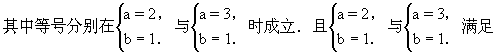
(Ⅰ)所以f(-2)的取值范围是[6,10].
解法二(数形结合)

建立直角坐标系aob,作出不等式组(Ⅰ)所表示的区域,如图6中的阴影部分.因为f(-2)=4a-2b,所以4a-2b-f(-2)=0表示斜率为2的直线系.如图6,当直线4a-2b-f(-2)=0过点A(2,1),B(3,1)时,分别取得f(-2)的最小值6,最大值10.即f(-2)的取值范围是:6≤f(-2)≤10.
解法三(利用方程的思想)
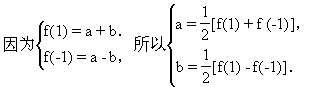
又f(-2)=4a-2b=3f(-1)+f(1),而
1≤f(-1)≤2,3≤f(1)≤4, ①
所以 3≤3f(-1)≤6. ②
①+②得4≤3f(-1)+f(1)≤10,即6≤f(-2)≤10.
说明:(1)在解不等式时,要求作同解变形.要避免出现以下一种错解:
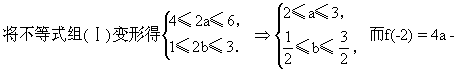
2b,8≤4a≤12,-3≤-2b≤-1,所以 5≤f(-2)≤11.
(2)对这类问题的求解关键一步是,找到f(-2)的数学结构,然后依其数学结构特征,揭示其代数的、几何的本质,利用不等式的基本性质、数形结合、方程等数学思想方法,从不同角度去解决同一问题.若长期这样思考问题,数学的素养一定会迅速提高.
例5.如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状。
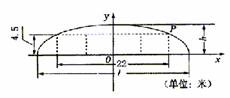 (1)若最大拱高h为6米,则隧道设计的拱宽
(1)若最大拱高h为6米,则隧道设计的拱宽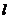 是多少?
是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽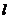 ,才能使半个椭圆形隧道的土方工程最小?
,才能使半个椭圆形隧道的土方工程最小?
(半个椭圆的面积公式为s=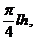 柱体体积为:底面积乘以高,
柱体体积为:底面积乘以高,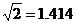 ,
,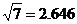 本题结果均精确到0.1米)
本题结果均精确到0.1米)
分析:本题为2003年上海高考题,考查运用几何、不等式等解决应用题的能力及运算能力。
解:1)建立如图所示直角坐标系,则P(11,4.5)
椭圆方程为: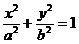
将b=h=6与点P坐标代入椭圆方程得
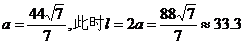 故隧道拱宽约为33.3米
故隧道拱宽约为33.3米
2)由椭圆方程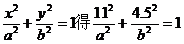
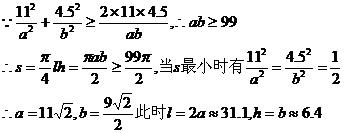
故当拱高约为6.4米,拱宽约为31.1米时,土方工程量最小.
例6.已知n∈N,n>1.求证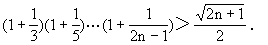
分析:虽然待证不等式是关于自然数的命题,但不一定选用数学归纳法,观其“形”,它具有较好规律,因此不妨采用构造数列的方法进行解.
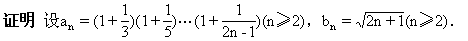
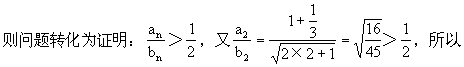

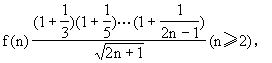
则
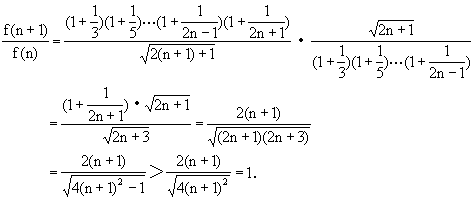

说明:因为数列是特殊的函数,所以可以因问题的数学结构,利用函数的思想解决.
预计2010年的高考主要有以下几点:(1)不等式的性质是进行不等式的变换、证明不等式的依据,所以它仍是高考的一个重点内容,常以选择题、填空题形式出现:(2)解不等式主要与求函数的定义域、值域问题及单调性相结合;(3)不等式的证明基本上与数列结合,另外还用注意利用导数证明不等式。
(1)不等关系
了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景.
(2)一元二次不等式
① 会从实际情境中抽象出一元二次不等式模型.
② 通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系.
③ 会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.
(3)二元一次不等式组与简单线性规划问题
① 会从实际情境中抽象出二元一次不等式组.
② 了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.
③ 会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.
(4)基本不等式: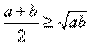
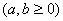
① 了解基本不等式的证明过程.
② 会用基本不等式解决简单的最大(小)值问题.
(1)理解不等式的性质及其证明.
(2)掌握两个正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用.
(3)掌握分析法、综合法、比较法证明简单的不等式.
(4)掌握简单不等式的解法.
(5)理解不等式│a│-│b│≤│a+b│≤│a│+│b│.
5、含绝对值的不等式.
4、不等式的证明
3、不等式的解法(特别一元二次不等式(特别是含参数)的解法).
2、不等式的基本性质
1、不等式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com