8．如果把直角三角形的三边都增加同样的长度，则这个新的三角形的形状为　　 (　)

A．锐角三角形 　　　B．直角三角形　　 C．钝角三角形　 　D．由增加的长度决定

解析：设增加同样的长度为x，原三边长为a、b、c，且c²＝a²+b²，a+b>c新的三角形的三边长为a+x、b+x、c+x，知c+x为最大边，其对应角最大．

而(a+x)²+(b+x)²－(c+x)²＝x²+2(a+b－c)x>0，由余弦定理知新的三角形的最大角的余弦为正，则为锐角，那么它为锐角三角形．

答案：A

7.在△ABC中，角A、B、C所对的边分别为a，b，c，如果c＝a，B＝30°，那么角C等于　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　(　)

A．120°　 　　B．105°　　 C．90°　　 　D．75°

解析：∵c＝a，∴sinC＝sinA＝sin(180°－30°－C)＝sin(30°+C)＝(sinC+cosC)，

即sinC＝－cosC.∴tanC＝－.又C∈(0,180°)，

∴C＝120°.

答案：A

6．某人在山顶观察地面上相距2 500 m的A、B两个目标，测得目标A在南偏西57°，俯角为30°，同时测得B在南偏东78°，俯角是45°，求山高(设A、B与山底在同一平面上，计算结果精确到0.1 m)．

解：画出示意图(如图所示)

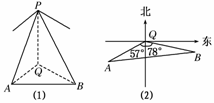
设山高PQ=h，则△APQ、△BPQ均为直角三角形，

在图(1)中，∠PAQ=30°，∠PBQ=45°.

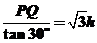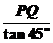∴AQ=，BQ==h.

在图(2)中，

∠AQB=57°+78°=135°，AB=2 500，

所以由余弦定理得：

AB²=AQ²+BQ²-2AQ·BQcos∠AQB，

即2 500²=(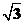h)²+h²-2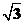h·h·cos135°=(4+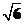)h²，

∴h=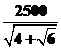≈984.4(m)．

答：山高约984.4 m.

5．在一个塔底的水平面上某点测得该塔顶的仰角为θ，由此点向塔底沿直线行走了30 m，测得塔顶的仰角为2θ，再向塔底前进10 m，又测得塔顶的仰角为4θ，则塔的高度为________．

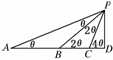
解析：如图，依题意有PB=BA=30，PC=BC=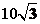.在三角形BPC中，由余弦定理可得

cos2θ=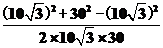

=，所以2θ=30°，4θ=60°，在三角形PCD中，

可得PD=PC·sin4θ=10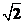·=15(m)．

答案：15 m

4.据新华社报道，强台风“珍珠”在广东饶平登陆．台风中心最大风力达到12级以上，大风降雨给灾区带来严重的灾害，不少大树被大风折断．某路边一树干被台风吹断后，折成与地面成45°角，树干也倾斜为与地面成75°角，树干底部与树尖着地处相距20米，则折断点与树干底部的距离是　　　　　　　　　　　　　　　　　　　 (　)

A.米　　　 　B．10米　　　 C.米　 　　　　　D．20米

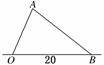解析：如图，设树干底部为O，树尖着地处为B，折断点为A，

则∠ABO=45°，∠AOB=75°，

∴∠OAB=60°.

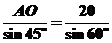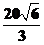由正弦定理知，，∴AO= (米)．

答案：A

3．如图所示，为了测量河对岸A，B两点间的距离，

在这一岸定一基线CD，现已测出CD＝a和∠ACD＝60°，

∠BCD＝30°，∠BDC＝105°，∠ADC＝60°，试求AB的长．

解：在△ACD中，已知CD＝a，∠ACD＝60°，∠ADC＝60°，所以AC＝a.　　 ①

在△BCD中，由正弦定理可得

BC＝＝a.　　　　　　　　　　　　　　　　　　　　 　　　　②

在△ABC中，已经求得AC和BC，又因为∠ACB＝30°，

所以利用余弦定理可以求得A、B两点之间的距离为

AB＝＝a.

2．一船以每小时15 km的速度向东航行，船在A处看到一灯塔M在北偏东60°方向，行驶4 h后，船到达B处，看到这个灯塔在北偏东15°方向，这时船与灯塔的距离为________km.

解析：如图，依题意有AB＝15×4＝60，∠MAB＝30°，∠AMB＝45°，在△AMB中，由正弦定理得＝，解得BM＝30 km.

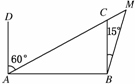
答案：30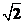

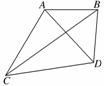
1.一船自西向东航行，上午10时到达灯塔P的南偏西75°、距塔68海里的M处，下午2时到达这座灯塔的东南方向的N处，则这只船航行的速度为　　　　　　　 (　)

A.海里/时　 　　　　　　B．34海里/时

C.海里/时 　　　　　　　D．34海里/时

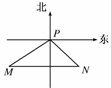解析：如图．由题意知∠MPN=75°+45°=120°，∠PNM=45°.

在△PMN中，由正弦定理，得

，

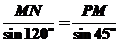∴MN=68×=34.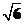

又由M到N所用时间为14-10=4小时，

∴船的航行速度v= 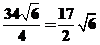(海里/时)．

答案：A

20. (本题满分16分)已知函数

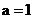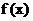(1) 当时, 求的最小值;

(2) 若直线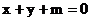对任意的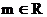都不是曲线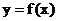的切线, 求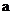的取值范围;

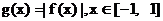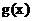(3 )设, 求的最大值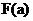的解析式.

19. (本题满分16分)某地为促进淡水鱼养殖业的发展, 将价格控制在适当范围内, 决定对

淡水鱼养殖提供政府补贴. 设淡水鱼的市场价格为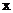元/千克, 政府补贴为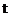元/千克. 根

据市场调查, 当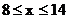时, 淡水鱼的市场日供应量P千克与市场日需求量Q千克近似

地满足关系: ,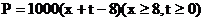

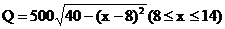
(1) 当时的市场价格称为市场平衡价格. 将市场价格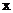表示为政府补贴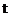的函数, 并

求出函数的定义域.

(2) 为使市场平衡价格不高于每千克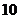元, 政府补贴至少为每千克多少元？