3．某学校高一年级500名学生中，血型为O型的有200人，A型的有125人，B型的有125人，AB型的有50人，为了研究血型与色弱之间的关系，用分层抽样的方法抽取一个容量为40的样本，则在血型为O型的学生中应抽取　　　　 人。

2．已知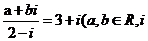为虚数单位)，则=　　　　 ．

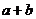1．记函数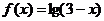的定义域为A，则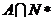中有　　　 个元素。

12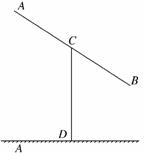．(2010·宁波模拟)某建筑的金属支架如图所示，根据要求

AB至少长2.8 m，C为AB的中点，B到D的距离比CD

的长小0.5 m，∠BCD＝60°，已知建造支架的材料每米

的价格一定，问怎样设计AB，CD的长，可使建造这个

支架的成本最低？

解：设BC＝am(a≥1.4)，CD＝bm，连接BD.

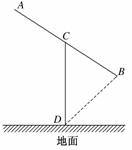则在△CDB中，(b－)²＝b²+a²－2abcos60°.

∴b＝.

∴b+2a＝+2a.

设t＝a－1，t≥－1＝0.4，

则b+2a＝+2(t+1)＝3t++4≥7，

等号成立时t＝0.5＞0.4，a＝1.5，b＝4.

答：当AB＝3 m，CD＝4 m时，建造这个支架的成本最低．

11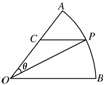．如图，扇形AOB，圆心角AOB等于60°，半径为2，

在弧AB上有一动点P，过P引平行于OB的直线和OA交于点C，设∠AOP＝θ，求△POC面积的最大值及此时θ的值．

解：因为CP∥OB，所以∠CPO＝∠POB＝60°－θ，∴∠OCP＝120°.

在△POC中，由正弦定理得

＝，∴＝，所以CP＝sinθ.

又＝，∴OC＝sin(60°－θ)．

因此△POC的面积为

S(θ)＝CP·OCsin120°＝·sinθ·sin(60°－θ)×

＝sinθsin(60°－θ)＝sinθ(cosθ－sinθ)

＝[cos(2θ－60°)－]，θ∈(0°，60°)．

所以当θ＝30°时，S(θ)取得最大值为.

10．线段AB外有一点C，∠ABC＝60°，AB＝200 km，汽车以80 km/h的速度由A向B行驶，同时摩托车以50 km/h的速度由B向C行驶，则运动开始________h后，两车的距离最小．解析：如图所示：设t h后，汽车由A行驶到D，摩托车由B行驶到E，则AD=80t，BE=50t.

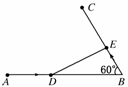因为AB=200，所以BD=200-80t，

问题就是求DE最小时t的值．

由余弦定理：DE²=BD²+BE²-2BD·BEcos60°

=(200-80t)²+2500t²-(200-80t)·50t

=12900t²-42000t+40000.

当t=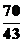时DE最小．

答案：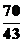

9.有一山坡，坡角为30°，若某人在斜坡的平面上沿着一条与山坡底线成30°角的小路前进一段路后，升高了100米，则此人行走的路程为　　　　　　　　　　　　 (　)

A．300 m 　　　　B．400 m　　　　 C．200 m　　　 　D．200 m

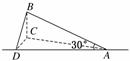解析：如图，AD为山坡底线，AB为行走路线，BC垂直水平面．

则BC=100，∠BDC=30°，∠BAD=30°，

∴BD=200，AB=2BD=400 米．

答案：B